Расчет времени нагрева и охлаждения тел конвекцией
 23 июля, 2016
23 июля, 2016  admin
admin Конвективный теплообмен — процесс передачи тепла движущейся газовой или жидкой средой. В самой движущейся среде передача тепла осуществляется теплопроводностью. Конвективный теплообмен в общем случае описывается системой дифференциальных уравнений теплопроводности в движущейся среде, движения вязкой - ЖИДКОСТИ, непрерывности для жидкости и условиями однозначности.
Решение системы дифференциальных уравнений представляет большие трудности, поэтому с помощью теории подобия отдельные ^физические величины объединяют в безразмерные комплексы:
 Физический смысл критерия
Физический смысл критерия
Отношение тепловой проводимости на границе тело — среда к тепловой проводимости среды Подъемная сила нагретой среды при естественной конвекции Отношение теплоты- конвекции к теплоте, которая передается теплопроводностью
Отношение сил инерции к силам вязкого трения
Отражает физические свойства среды
Это позволяет перейти к системе безразмерных дифференциальных уравнений, решение 'которых определяет функциональную связь критериев (независимые комплексы) и чисел подобия, включающих в себя определяемую величину: Nu=f(Gr, Рт, Ре).
Для естественной конвекции справедлива зависимость Nu= =f(Gr, Pr)".
Величина критерия Прандтля практически не зависит от температуры н давлення, а зависит от атомарности газа:
Атомарность газа 1 2 3 4
Рг 0,67 0,72 0,80 1,00
Коэффициенты Сип имеют следующие значения:
Pr, Gr. . . МО-3—5 102 5-10*—2-Ю7 2-Ю7—1013
С........................ 1,180 0,540 0,135
п........................ 1/8 1/4 1/3
![]()
|
|
|
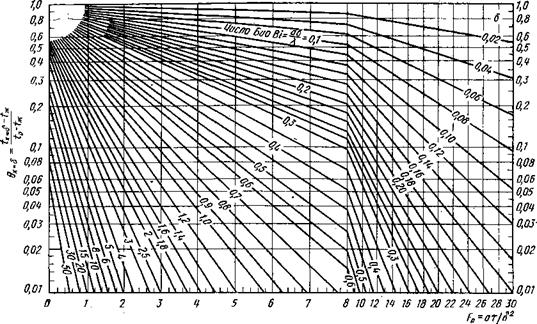
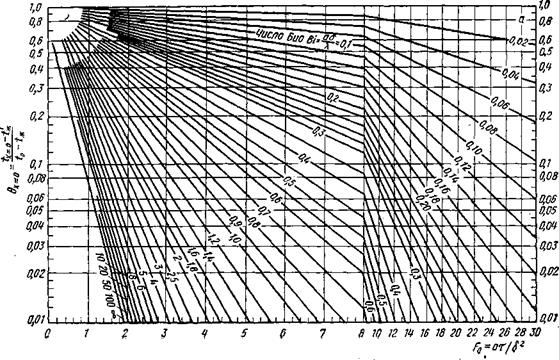
Рис. 35. Графическое |
|
рещение уравнения (12) для поверхности (я) н середины (б) пластины |
Величина критерия Грасгофа рассчитывается по таблицам. Таким образе»*, число Нуссельта определяет значение коэффициента теплоотдачи конвекцией ак.
Время нагрева н охлаждения теплотехнически тонкого тела рассчитывается по формуле
тн = (Мс/ак) lg [( Т0.с - Т„)/( Г0.с - Гк)] , (3)
где М — массивность тела, кг/м2; с — удельная теплоемкость паяемого материала, Дж/(кг-К); Т0.с—температура окружающей среды, К; Тн, Тк—начальная и конечная температуры тела, К.
Время нагрева теплотехнически толстого тела конвекцией и изменение температурного поля по объему тела определяются теплопроводностью. Коэффициент теплоотдачи конвекцией определяет граничные условия 3-го рода. Для вынужденной конвекции число Нуссельта находится в функциональной зависимости от критериев Рейнольдса и Прандтля: Nu=f(Re, Рг).
Расчетные формулы числа Нуссельта и критериев подобия для тел простой формы и ламинарного или турбулентного характера движения среды приведены в работе [84].
Расчет времени, охлаждения деталей при радиационном теплообмене
Величина лучистого теплового потока определяется температурой источника энергии. Предположим, что при радиационном теплообмене температура окружающей среды постоянная (T0.e=const) н тепловая энергия, передаваемая изделию, поглощается нм без потерь. В этом случае уравнение, выражающее закон сохранения энергии, принимает вид [84]:
![]()
![]()
![]() r4) = fllcil,
r4) = fllcil,
От
 |
где v—функция, зависящая от отношения температуры окружающей среды. Так, если 7’i/7’o. c=0,2, то функция v=Tr[To e. Индексы «к» и «н» относятся к температуре тела в конце и начале нагрева соответственно.
Время охлаждения теплотехнически тонкого изделия определяется по формуле (4), однако в этом случае нужно поменять знаки перед v„ и v„. Расчет времени нагрева и охлаждения теплотехнически толстого изделия относится к сложному теплообмену н изложен в следующем разделе.
Расчет времени нагрева и охлаждения паяемого изделия при сложном теплообмене
Радиационно-кондуктивный теплообмен. Типичным примером радиа - цнонно-кондуктивного теплообмена может служить нагрев в индукционных нагревательных установках
Тепловая энергия от индуктора к паяемому изделию передается ^излучением. Электродвижущая сила, наведённая в поверхностном слое изделия, создает поле переменного тока, которое обусловливает/® Проводнике выделение джоулевого тепла. Поэтому, расчет радиацнониО-коидуктивного теплообмена ведут в две стадии: на Первой оиределяют лучистый тепловой'потея, поглощаемый изделием (граничное условие 2-го рода), илн температуру поверхности паяемого изделия; на второй—рассчитывают времи нагрева или охлаждения Паяемого изделия теплопроводностью с граничными условиями, ояределеЯнымв на первой стадии:
Если' граничное условие представлено в виде постоянного во времени теплового потока, то время нагрева паяемого изделвя рассчитывается по формуле
V= £- [S К!) - s (d, Q)] }, (5)
где d — диаметр Нагреваемого изделия, mi S—'функция, значения которой даны в работе [84].
Если граничное условие задано в виде постоянной температуры на поверхности паяемого изделия, то время нагрева определяется теплопроводностью.
Радиационно-конвективный - теплообмен. Этот - вид теплообмена имеет место при нагреве паяемых изделий в печах сопротивления с принудительной подачей газа для низкотемпературной пайки.
Цель расчета радиационно-конвективного теплообмена состоит в определении суммарного коэффициента теплоотдачи ат, который- учитывает теплообмен между нагреваемым телом и окружающей. средой конвекцией н излучением.
Для практических расчетов радиационно-конвективного теплообмена удобно пользоваться графиками, построенными на основе расчета коэффициентов теплоотдачи.
Определив величину суммарного коэффициента теплоотдачи как ат“=ак+ажаи, рассчитывают величину критерия Вио.
Расчет времени нагрева и охлаждения изделия — теплотехнически тонкого тела— проводят по формул* (б),-в которой вместо коэффициента теплоотдачи конвекцией ак надо поставить аначеиие суммарного коэффициента теплоотдачи ат-
Время нагрева и охлаждения теплотехнически толстого тела определяется теплопроводностью. Расчет этого времени приведен - выше. Значение суммарного коэффициента теплоотдачи-в этом случае определяет граничное условие третьего рода. Рассмотренные методики расчета времени и нагрева н охлаждения справедливы для бесконечных пластины, цилиндра и шара. В практике нагрева :Прн пайке имеют дело с изделиями конечной формы. При этом заменяют паяемое изделие иа тело конечных размеров простой формы поверхности (параллелепипед, прямоугольный стержень, цилиндр, и шар).
Параллелепипед конечных размеров можно рассматривать как тело, образованное пересечением бесконечных пластин. Поэтому метод расчета, относящийся к бесконечной пластине, можно отисстн И к параллелепипеду. Это положение подтверждено правилом перемножения температурных критериев [84], иоторо* определяет относительную температуру сплошного изделия конечных размеров как произведение относительных температур трёх бесконечных пластин.
Относительная температура цилиндра конечных размеров равив произведению относительных температур неограниченного цилиндра и пластаны.
Расчет критерия Био по трем координатным осям показывает, в каком направлении имеет место наибольшее изменение температурь»: чем меньше значения критерия Био, тем быстре^ измеияется температура по сечению детали или изделия. Расчет времени нагрева н охлаждения следует начинать дйя минимального значения критерия Био, так как в этом случаеіначгргельно сокращается число расчетных точек. Расчет ведут обычно до момента времени, при котором значение относительной температуры 0<О,1.
Величину перепада температур АТ, К, между поверхностью и центром цилиндрического тела при его нагреве в индукторе при условии постоянства температуры на его поверхности в зависимости от времени нагрева определяют по формуле А/=7V 1,61 ехр(—5,8Г*), где Го—-критерий Фурье (Ро>0,3).
Для сохранения постоянства температуры на поверхности массивной детали при индукционном нагреве последний ведут с перерывами, чтобы избежать плавления нагреваемой детали с поверхностью. Глубинный нагрев металла при индукционном нагреве подчиняется законам теплопередачи теплопроводностью. Скорость. индукционного нагрева связана с глубиной проникания тока'
 Опубликовано в Проектирование технологии пайки металлических изделий
Опубликовано в Проектирование технологии пайки металлических изделий Комментарии закрыты.