Рекомендуется следующий порядок определения точности, кото­рый можно применить для микродоза гора жидкости [Л. 55—68]: 1. Производится серия замеров расходов Qi в различных точ­ках статической характеристики. Количество замеров должно быть не менее 25—30. 2. Из числа замеров исключаются значения Qi, имеющие значи­тельные отклонения. 3. Подсчитываются среднеарифметические значения:

(28)

где Qi — подача микродозатора; п — число замеров, входящих в каждую серию опытов. 4. Определяется среднеквадратичное отклонение каждой серии замеров:

П 2 (<3i-Q)2

(29)

5. При помощи критерия %2 проверяется гипотеза нормальности закона распределения погрешностей:

п

(mi — пРу tiPi

(30)

где ті — число наблюдений, приходящихся на интервал i> Pi — вероятность попадания в і-й интервал. 6. Рассчитывается точность микродозирования в различных точ­ках статической характеристики микродозатора:

'макс

(31)

»

где X — коэффициент, зависящий от надежности и числа замеров п в серии, который выбирается по таблицам Стьюдента — Фишера [Л. 63]; QM акс — максимальное значение расхода в данном режиме микродозатора. При исследовании точности микродозирования необходимо рас­смотреть статическую или тарировочную характеристику микродоза­тора Q=HO, (32) где Q — расход микродозатора; / — ток в цепи питания микродо­затора. Статическая характеристика определяется для конкретных пара­метров микродозатора (ток, вязкость, плотность и температура мик - родозируемой жидкости). Изменение параметров технологического процесса или измене­ние режимов работы микродозатора крайне усложняет его воз­можные перенастройки. Однако в каком-то диапазоне изменения вы-

параметров статическая характеристика меняется в до­пустимых пределах точности микродозирования.

Одной из задач экспериментального исследования микродозатора является определение зависимости диапазона изменения режимов работы микродозатора от точности микродозирования, чтобы в даль­нейшем учитывать ее при перенастройке работы микродозатора для различных условий эксплуатации. Все это имеет место при нормальном законе распределения погрешности. Однако распре­деление погрешности при эксплуатации микродозатора может от­личаться от нормального закона. В этом случае погрешность опре­деляют энтропийным способом.

іВ технике применяются приборы, с помощью которых проводят измерения лишь с определенной заданной точностью — допустимой основной погрешностью. Величина допустимых основных погреш­ностей, соответствующая нормальным условиям работы приборов, устанавливается ГОСТ и выражается обычно в относительных ве­личинах.

(Погрешности приборов могут зависеть также от значения из­меряемой величины и, следовательно, быть различными для раз­личных показаний приборов.

Так, например, у интегрирующих приборов погрешность пока­заний, при прочих равных условиях, пропорциональна значению измеряемой величины {Л. 58—60].

іііод абсолютной погрешностью показаний прибора 6 понимает­ся разность между показанием прибора Qu и действительным зна­чением величины Q:

6 = Qn-Q.

,По допустимой основной погрешности измерительные приборы подразделяются по классам точности.

Условное обозначение класса точности R соответствует наи­большей основной допустимой абсолютной погрешности 6м акс* ОТ - НесеННОЙ к соответствующему предельному значению шкалы при­бора JV, выраженной в процентах, т. е.

* = Де-ню. (33)

/Практически наибольшая допустимая погрешность бМакс при­бора равна половине цены деления шкалы.

.При пользовании лабораторными приборами следует с целью повышения точности исключить из них систематические погреш­ности (учитывающие как состояние прибора, так и влияние среды) внесением поправок, определяемых либо на основании физических закономерностей, присущих прибору, либо устанавливаемых провер­кой, т. е. сравнением показания прибора с показаниями образцово­го прибора. Для образцовых приборов исключение систематических погрешностей производится заводом-изготовителем, который снаб­жает прибор свидетельством, устанавливающим зависимость между действительными значениями измеряемой величины и показаниями прибора, а также класс точности прибора.

(Если прямое измерение некоторой величины не осуществимо или затруднено, прибегают к косвенному измерению ряда незави­симых величин, связанных с данной величиной некоторой функци­ональной зависимостью #=*/(*і; х2; ..хп) [Л. 61, 62, 70].

Если известна погрешность измерений величин Xu Х2, . • • ,Хп, ТО можно определить и погрешность измерения величины у.

Погрешность косвенных измерений принято оценивать относи­тельной среднеквадратичной погрешностью бо/, которая вычисля­ется по формуле

воf = ± + ®20jc, + • • • + S20xn' (34)

где д0Хі, 50л. а, . . д0Дя — относительные среднеквадратичные погреш­ности измерений величин Хі, Х2 Хп

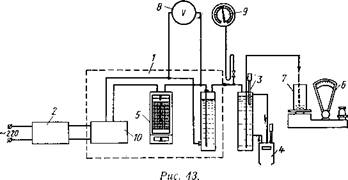
Для определения погрешности микродозатора применяется экспериментальная установка, где в качестве рабочего агента взята вода (рис. 43).

Микродозатор 7, питаемый через стабилизатор напряжения 2, осуществляет дозирование жидкости из емкости 3 с термостатом

4. Температура дозируемой жидкости измеряется контактным тер­мометром 10 со шкалой 0—50^С. Расход регистрируется самопишу­щим миллиамперметром 5. Для измерения напряжения и давления (газов электролиза) в схему соответственно включены вольтметр 8 и образцовый манометр 9.

Для измерения подачи микродозатора 1 использованы техниче­ские весы 6, где помещен мерный сосуд 7.

іВ каждой серии измерений проводилось не менее 26—30 отдель­ных наблюдений. Всего проведено более (170 серий замеров на различных режимах работы микродозатора.

Точность измерений потребовала значительной затраты времени, каждая серия измерений продолжалась от 8 до 15 ч.

Способ измерения расхода микродозатора Qi с помощью весов заключался в том, что соответствующим измерением массы опре­деляется количество жидкости, протекающей через систему за не­который промежуток времени, длительность которого определяется счетчиком времени (обычно секундомером).

Измерения проводились с помощью циферблатных весов ВНЦ-2, имеющих класс точности 1, с пределом взвешивания до 2 кг с верх­ним пределом измерения 200 г, ценой деления шкалы 2 г. Допус­тимая погрешность при взвешивании до 500 г не более ±0,1%, при взвешивании до 200 г не более ±0,1% фактической нагрузки. Для сглаживания колебаний стрелки весы снабжены демпфером. Время определялось секундомером 51СД (класс точности 1). Цена деления шкалы секундомера составляет 0,1 с, а цена деления шкалы минутного счетчика 0,5 мин. Средняя поправка хода секун­домера при температуре +20°С составляет за 30 с — 0 и за 15 мин — 0,1 с. Измерения производились при фиксированных зна­чениях t к Q для каждой серии опытов. Например при /=1800 с, Q = 305 г (/=11000 мА) погрешность

0,Ы00 Л 0,1-100

§t — 1800 = 0,0055 °/oj 8q = 000 =0,032 %;

а - Vtet + h*Q = Y0,0055s + 0,0322 = 0,0325»/».

Ток / измерялся регистрирующим миллиамперметром (класс точности 1, тип Н359).

Таблица 5 Ко п. п. Q, мл/ч Ко. п/п. Q, мл/ч по порядку по возрастанию по порядку по возрастанию 1 0,304 0,298 14 0,301 0,308 2 0,314 0,300 15 0,311 а, 308 3 0,300 0,300 16 0,314 0,309 4 0,302 0,301 17 0,308 0,310 5 0,310 0,302 18 0,303 0,310 6 0,305 0,302 19 0,309 0,311 7 0,315 0,303 20 0,304 0,311 8 0,300 0,304 21 0,313 0,313 9 0,314 0,304 22 0,313 0,313 10 0,302 0,305 23 0,308 0,314 11 0,307 0,305 24 0,311 0,314 12 0,310 0,305 25 0,305 0,314 13 0,305 0,307 26 0,298 0,315

Температура дозируемой жидкости при помощи термостата 4 во время опыта поддерживалась постоянной с допуском ±0,2РС, а измерение температуры производилось термометром класса точ­ности ОД со шкалой 0—50°С.

-Измерения производились при температуре 20±0,1°С и относи­тельные погрешности при этом составили:

откуда общая погрешность установки

«0/ = /0,03252 + 0,12 + 0,52 = 0,51 %.

Приведем пример обработки статистических данных.

Результаты одной серии измерений приведены в табл. 5. Полу­ченные данные сначала систематизируются, т. е. располагаются пэ порядку их_возрастания, затем вычисляются оценки математического ожидания Q и дисперсии o2q:

(35)

<*=4-2

1 = 1

s №-<?)2

(36)

CF 2л

/=1___________________

П — 1

Для нашего примера Q=0,3077; g2q = 2,48-10-5.

Затем строится гистрограмма. При этом необходимо выбрать и установить количество столбцов гистрограммы не менее б—7, так как при меньшем количестве столбцов трудно выявить характерные черты статистического распределения [Л. 63]. Однако при увеличе­нии количества столбцов требуется проводить значительно большее количество опытов, так как на каждый столбец должно приходиться не менее трех-четырех результатов измерения. Ширина столбца опре­деляется по формуле

, Фмакс — Qmhb

й ~ 1 + 3,322 lg п ’

где Qmhh и <2макс — минимальное и максимальное значения рас­хода систематизированного ряда.

Подставляя в (37) значения опытов, получаем */=0,003.

Для вычисленной ширины столбца выбираем границы и пред­ставляем данные в виде статистического ряда (табл. 6), где т* —

Таблица 6

№ п. п.	Qi	Q/+i	т1	pi	nPt
1	0,300	0,301	4	0,0292	0,7592
2	0,301	0,304	5	0,1393	3,6218
3	0,304	0,307	4	0,2173	3,6498
4	0,307	0,310	5	0,2328	6,0528
5	0,310	0,313	4	0,1790	4,6540
6	0,313	0,315	4	0,0701	1,8226

число наблюдений, приходящихся на і-й интервал. Вероятность Pi, соответствующая 1-му интервалу, определяется по формуле

Рі=і!7Г - (38)

Построенная гистограмма представлена на рис. 44.

Так как вид гистограммы близок к нормальному распределе­нию, то необходимо рассчитать критерий согласия %2, по значению которого можно будет принять или отвергнуть гипотезу о распреде­лении погрешности по закону Гаусса.

Пользуясь параметрами нормального закона распределения (5=0,3077; о2 = 10-5 -2,48), находим вероятности попадания в интер­вал по формуле

'Q/ч

- Q

(39)

Ф

Pi

Ф

0,675aQ

( Qj — Q V0>675aQ

где Qi, Qi+1—границы /-го интервала; Ф (х)—приведенная функция Лапласа [Л. 61].

По формуле, приведенной в [Л. 63], находим:

(ті — пРі)*

X2

пРі

= 17,08,

i=l

где Pi — вероятность попадания в j-й интервал.

Число степеней свободы определяется по формуле

Г = /—5 = 3,

где s — число наложенных связей; / — число интервалов.

Для г—3 при х2 —17,08 Рі = 0,001.

Так как вероятность Pi=0,001 очень мала, то экспериментальные

Qi

данные следует признать противо­речащими гипотезе о том, что - ве­личина Qi распределена по нор­мальному закону.

Поэтому необходимо опреде­лить точность дозирования при - помощи энтропийного метода, ко­торый ириігоден для любого зако­на распределения.

Qi На основании данных табл. 6 0,300 ' Щ ‘ 0,310 ‘ 0316 мл/чдля одинаковой ширины столбцов 0301 0,307 0J13 гистограммы эн. тропииное значе-

' * 9 ние погрешности определяется по

Рис. 44. формуле

А = -

— 0,0089.

(40)

Для облегчения расчетов составляем табл. 7.

После определения Л необходимо приблизительно оценить сред­неквадратическое значение погрешности:

41)

о = -£- = 0,0051.

Энтропийный коэффициент микродозатора k находится в преде­лах (1,7±0,3 [Л. 69].

Таблица 7 № п. п. п1 Р=п± п при п=26 1 п р~ч при /1=26 № 1 0,5 0,0192 52,0 1,077 2 1,0 0,1384 26,0 1,133 3 1,5 0,0577 17,3 1,179 4 2,0 0,0770 13,0 1,218 5 2,5 0,0960 10,4 1,252 6 3,0 0,1150 8,67 1,252 7 3,5 0,1346 7,44 1,309 8 4,0 0,1540 6,50 1,334 9 4,5 0,1730 5,78 1,355 Ю 5,0 0,1920 5,20 1,371 11 5,5 0,2115 4,73 1,389 12 6,0 0,2300 5,34 1,402 13 6,5 0,250 4,00 1,414 14 7,0 0,269 3,715 1,422 15 7,5 0,288 3,47 1,430 16 8,0 0,308 3,25 1,438 17 8,5 0,327 3,06 1,442 18 9,0 0,346 2,89 1,443 19 9,5 0,366 2,74 1,444 20 10,0 0,385 2,60 1,445 21 10,5 0,44 2,48 1,442 22 11,0 0,424 2,36 1,440 23 11,5 0,442 2,26 1,434 24 12,0 0,462 2,17 1,430 25 12,5 0,481 2,08 1,424 26 13,0 0,500 2,00 1,421

В заключение расчета определяется точность микродозатора:

Л*д = ±р~!------------------- 100»/.. (42)

V Ломакс

Таким образом, точность микродозатора для данной серии опы­тов соответствует [Л. 71]

Лід = 0,55 o/Q.