/ >

А. Противоток и прямоток

Поверхность нагрева

Ниже будет рассмотрен случай прямотока и противотока. Са­мым простейшим случаем расчета является случай, когда даны температуры обеих сред на входе и выходе и нужно рассчитать количество передаваемого тепла. Тогда количество тепла, пере­данного в час,

TOC o "1-5" h z фг = вГ • сг (/г1 — /г2) ккал/час (442)

Или по отношению к тепловоопринимающей среде

Фв = св • Св • (*В1 — *вг) ккал/час. (442а

Ч

Необходимая поверхность нагрева определяется из уравнения) (3 = ^ . Д /ср ккал/час (443)

или

Здесь и в дальнейшем:

К - коэффициент теплопередачи [уравнение (29) и стр. 42], ккал/м2 • час°С;

—общая поверхность нагрева, м2

Д/ср —средняя разность между температурами протекающих потоков;

<3Г —количество более нагретой среды, кг/час;

V г—объем более нагретой среды, мъ/час сг —удельная теплоемкость более нагретой сре - ды, ккал/кг»°С вГ - сГ = —водяное число более нагретой среды,

Ккал/час • °С;

£в —количество более холодной среды, кг/час;

Ув —объем более холодной среды, мъ! час св— удельная теплоемкость более холодной среды, ккал/час [182]°С;

Сь-св = №в—водяное число более холодной среды, ккал/час • °С;

/п —температура более нагретой среды на входе, °С; tГ2 —температура более нагретой среды на выхо­де °С;

*ш1 —температура более холодной среды на входе, °С; *В2 —температура более холодной среды на выхо­де, °С;

Tr—температура более нагретой среды после омы - вания части поверхности нагрева 1?х м2, считая от входа, °С;

—температура более холодной среды в точке? х (считая от входа более нагретой среды), °С; е — основание натуральных логарифмов, равное 2,718.

Так как количество отданного тепла должно быть равно ко­личеству воспринятого*, то уравнения (442), (442а) и (443) равнозначны и их правые части могут быть приравнены. От­сюда получаем необходимую поверхность нагрева

TOC o "1-5" h z р== Ог - сг(/г1-(42) м2 5

К - Мср К ’

Или

Р — (*В1 ^вг) м2 (446)

________ к • А /ср_____________________ 1 7

Произведение бгсг или соответственно Оъсъ называют «во­дяным числом» и в дальнейшем обозначают через и Водяное число определенного количества вещества равно такому же количеству воды в килограммах, которое имеет та­кую же теплоемкость, что и рассматриваемое количество ве­щества. Два количества вещества характеризуются равными значениями теплоемкости, если они требуют р|авногр количества тепла в килокалориях для повышения температуры каждого из них на 1 °С. Без изменения числового значения № вместо кг можно подставлять также V мъ (если взять газ при нормальных условиях: 0°С и 760 мм рт. ст., то нм3). В этом случае удельная теплоемкость также должна быть отнесена к 1 м3, т. е. размер­ность с должна быть ккал/м3 • °С.

Чтобы, пользуясь уравнениями (445) и (446), по известным температурам на входе и выходе рассчитать необходимую по­верхность нагрева теплообменника, нужно еще определить среднюю разность между температурами обменивающихся теп­лом сред. При прямотоке она равна

(447)

А при противотоке

(448)

Оба эти уравнения с некоторым приближением можно заме­нить уравнением, справедливым для обоих случаев:

Д/ ^Г1 Ч~ ^Г2 ^В1 Ч~ ^В2 СР 9 о

(449)

Точность результатов, полученных по уравнению (449), будет тем выше, чем меньше изменение разности температур проте­кающих сред. При больших изменениях этой разности нужно применять уравнения (447) и (448) *. Уравнение (449) приме­нимо, если величина дроби под знаком логарифма колеблется в пределах от 0,7 до 1,6.

В этих уравнениях буквой «в» обозначены величины, относя­щиеся к более холодной среде (тепловоспринимающей) и бук­вой «г» — к более нагретой (теплоотдающей) среде. Обозначе­ния см. на рис. 49 и 50.

Очень часто поверхность нагрева в любой своей точке име­ет одинаковую температуру /0 (паровой котел, конденсаторы и т. п.); в этом случае уравнения (447) и (448) упрощаются и становятся идентичными, так как 1в1 =/в2 =t0 равны темпера­туре поверхности нагрева. Средняя разность температур по­верхности нагрева с постоянной температурой to и протекаю­щей среды с температурой на входе ^г1 и на выходе /Г2 опреде­ляется как

TOC o "1-5" h z Д, ср = --------------------------------- оС (450)

2,303 ^ —------ —

^Г2 - ^0

При небольших температурных изменениях это уравнение мож­но заменить следующим:

(451)

Знание средней разности между температурами протекаю­щих сред, а также разности между температурами протекаю­щей среды и поверхности нагрева необходимо, чтобы с помо­щью среднего коэффициента теплопередачи рассчитать коли­чество передаваемого тепла. Но часто известен лишь коэффи­циент теплопередачи и температуры протекающих сред на вхо­де, следовательно, не известны температуры на выходе, кото­рые нужны для расчета средней разности температур. Естест­венно, такой случай возникает всегда при расчете теплообмен­ника, для которого заранее не заданы внешними условиями все температуры на входе и выходе. В этих наиболее часто встречающихся случаях для расчета необходимой поверхности нагрева уравнения (444) — (450) применимы лишь с помощью метода последовательных приближений. Лучше найти юбщую кривую распределения температур, отражающую картину то­го влияния, которое оказывает изменение коэффициента тепло­передачи к и величины поверхности нагрева на эффективность теплообменника.

Температура теплообменивающихся сред

Температура теплоотдающей среды на выходе при прямо­токе равна

С. (453)

И температура тепловоспринимаюшей среды на выходе

1-е Н7Г

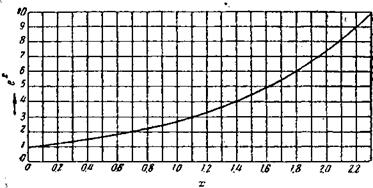
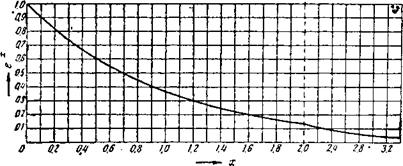
Выражения е+хи е~~х находят из рис. 51 и 52.

При противотоке температура теплоотдающей среды на вы­ходе равна

Или сокращенно

- «А - и ”(1-/) °с (454а) Хгг -"ЗС Рис. 51. Функция в

Рис. 52. Функция

И температура тепловоспринимающей среды на выходе

И = *П - «п - и------------------------- в. чгг - °С (455)

1 — Е - . е V,)

Ув

(455а)

Или сокращенно

^вг = ^г! (^п 4г) • / °С.

Выражение

1Рг

А •

(456)

Г е «"г

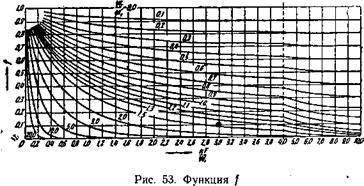
Зависит лишь от

. Поэтому его можно изобразить

Пучком кривых и определить просто из рис. 53.

Изменения температур tг и tв при прямотоке без труда оп­ределяются из уравнений (452) и (453), в которые вместо все*«

Поверхности нагрева ^ подставляют часть поверхности нагре­ва Рх м2, считая от входа, омываемую газом - Следовательно, / в прямоточном теплообменнике является температурой теп­лоотдающей среды после прохождения поверхности Рх м2, ко­торую определяют из уравнения (452) при условии, что Р=РХ. В противоточном теплообменнике замена Р на /г* неприемле­ма, .потому что при противотоке в теплообмене всегда прини­мает участие вся поверхность, в какой бы точке ни рассматри­валась температура. Изменение температуры теплоотдающей среды при противотоке

Изменение температуры тепловоспринимающей среды при про­тивотоке

И = - (*п - *в0---------- —------------ ; =гт—'9с. (458)

1 — — • в 1Гв

В этих уравнениях Т7* — поверхность нагрева, ж2, пройденная теплоотдающей средой от входа до рассматриваемой точки (см. рис. 50), Т7 — общая площадь поверхности нагрева, м2. Если в уравнение (457) подставить Рх = Р и в уравнение (458) ^*=0,

То температуры tг и tв будут обозначать температуры на вы­ходе tтъ и #в2 и уравнения будут аналогичны формулам (454) и (455).

Количество тепла, передаваемое за 1 час при прямотоке,

_ — /, +

[ *в)

Q=(^гl — tв^)^Wт•—— ---------------------- ккал/час. (459)

1+^7

Количество тепла, передаваемое за 1 час при противотоке,

К-Р

I

<2 = (^Г1 — /В1) • • --------------------- :----- — ккал/час (460)

_±£..Л__?г

И7Г *Р

1 — “ГГ - • е 1^в

Или после преобразования

<2 = (*п — tвl) ■ УРВ • (1 — /) ккал/час. (461)

Уравнения (454)—(458) и (460) будут неопределенными, если —— =1. Для этого нередко встречающегося в практике слу-

Иг в

Чая, применяя метод раскрытия неопределенностей (дифферен­цирование числителя и знаменателя), уравнения преобразуем следующим образом.

Для =1 изменение температуры теплоотдающей сре-

" в

Ды в противотоке Судет равно

«л - и-------------- °С. (462)

При подстановке /7л- = /г получаем температуру теплоотдающей среды на выходе:

*г2 = ~ (*п “ *в1) I— °С. (463)

1

Изменение температуры тепловоспришшающей среды при —-г— =1 можно определить из уравнения (443)

К •

1 + П7

TOC o "1-5" h z и = - «л - и------------- °с. (464)

1 + ~¥Г

Температуру тепловоспринимающей среды на - выходе опре­делим путем подстановки Рх = 0 в уравнение (464)

= *п - Уп -(в1)----------------------- °с. (465)

£ • г

1 + _гГ

Количество тепла, передаваемое при противотоке при —- =1,

(2 = (/г1— /в1)----- —------- ккал/час. (466)

Практически часто встречаются случаи, когда водяное чис­ло теплоотдающей среды УРГ или тепловоспринимающей сре­ды №в — бесконечно большая величина. Это всегда наблю­дается при температуре поверхности нагрева, постоянной во вре­мени и пространстве (паровой котел, испарители, конденсато­ры различных типов).

Очевидно, в этих случаях прямоток и противоток равноценны. Это подтверждается тем фактом, что уравнения (459) и (460) приводят к одинаковым результатам.

Если остающееся конечным водяное число обозначить через V?, то при 1ПОСТОЯН1НОЙ температуре и (поверхности нагрева или 1вторюй (протекающей - среды количество (передаваемого тепла

__ кР

1 = (гг1 — /0) №Г (1 — е ) ккал/час. (467)

И температура среды на выходе

_ ьр

№

*Й = *0 + (*Г1 —*о)-е г "С. (468)

В этих уравнениях:

К — коэффициент теплопередачи в случае,“когда tгo равно (постоянной температуре цреды 1при №г =оо, ккал/м2*час°С;

£ — коэффициент теплопередачи, в случае, когда равно постоянной температуре поверхности нагрева, ккал/м2*

• час• °С.

Кривые обеих функций е+х и е-х показаны на рис. 51 и 52. При помощи их можно легко определить количество передавае­мую • Р

Мого тепла, после того как рассчитаны показатели х =

И т. д. (числовой пример см. на стр. 464)*.

Коэффициент полезного действия теплообменника

Коэффициент полезного действия обычно определяется отно­шением

Количество действительно переданного тепла /лсп

— -- ;---------------------------------------------------------------- •

Максимальное количество тепла, которое можно передать

Максимально возможное количество тепла, очевидно, можно передать в теплообменнике с бесконечно большой поверхностью нагрева Р = со. Следовательно, для его определения в уравне-

^ • Р

Ния (459) и (460) необходимо подставить ——— = оо. Тогда

Получим по уравнению (459) максимально возможное количест­во передаваемого тепла при прямотоке:

Смаке= (^г1 ^1) ^ ккал/час. (470)

Такое же определение при противотоке по уравнению (460) дает два различных случая. Если ——— > 1, то показатель степени

" В

Функции е будет положительным и функция е при & • Т7 ОО будет равна не нулю, как это было бы при отрицательном показателе,

А бесконечности. Напротив, если ~г < 1, то функция е при

•*В

Неограниченно увеличивающемся £ • Т7 будет равна нулю. Для случая —г1- < 1 из уравнения (460) получим, что максималь-

" В

Ное количество тепла, которое можно передать при противотоке, Смаке = (*Г1 — 4х) * ккал/час. (471)

Если же —> 1» то максимальное количество тепла, которое

" в

Может быть передано,

^макс = (*п — ^В1) ккал/час. (472)

Максимальное количество тепла, передаваемого при прямотоке, зависит от температур на входе и от водяных чисел обеих сред. При противотоке это количество тепла зависит от температур на входе и меныиего водяного числа. Поэтому уравнения (471) и (472) можно объединить и определить максимальное количест­во тепла, передаваемого при противотоке,

(473)

Смаке = (^гХ — *ві) 147 мин ККОЛ/ЧОС,

Где №мин — наименьшее из водяных чисел УРГ и. С физичес­кой точки зрения уравнение (473) можно пояснить следующим образом. Максимально возможное изменение температуры сре­ды в г^ротивоточном теплообменнике по рис. 50 составляет /г1 — ^в1 °С. Максимальное количество тепла передается в том случае, если среда с меньшим водяным числом получит это изменение температуры.

Коэффициент полезного действия прямоточного теплообмен­ника по уравнению (469) получается делением уравнения (459) на (470)

(474)

Коэффициент полезного действия противоточного теплообмен­ника находим делением уравнения (460) на (473):

1 — е

(475)

Или после преобразования

Мин

(476)

№ При —- = 1 это уравнение будет (неопределенным. В опреде-

Т. е. чрезвычайно просто.

Передаваемое количество тепла по уравнению (469) для прямотока и противотока

<2 = . <2макс шал/час, (478)

Где г] и <2макс определяются из уравнений (470) и (474) или соответственно из (473) и (475) — (477).

Для расчета коэффициента полезного действия при прямото­ке пользуются рис. 52 [после определения показателя х —

К-Р! 1 , Гг 1 - О

= 1 + I, а при. противотоке — рис. 53.

Введение коэффициента полезного действия в эти расчеты на первый взгляд кажется ненужной сложностью 1по »сравнению с непосредственным расчетам количества передаваемого тепла. Однако это. неверно, (потому что знание коэффициента полезного действия наглядно дает представление о том, насколько теплооб­менник приближается к наилучшему теоретическому. коэффици­енту полезного действия, т. е. к 1. При г]=0,9 нет амьксл а увеличи­вать поверхность нагрева или коэффициент теплопередачи, так как дальнейшее приближение к г) = 1 происходит асимптотичес­ки, следовательно, только при увеличении поверхности нагрева до бесконечности можно было бы получить эти недостающие 10%. Но при этом не следует забывать, что тепловые потери, которыми здесь пренебрегаем, играют тем большую роль, чем больше г) при. прочих равных условиях. Следовательно, г) = 0,9 в большинстве случаев означает, что дальнейшее увеличение поверхности нагрева уже не экономично. Если бы нам было известно лишь количество переданного тепла, то нельзя было бы сделать такой вывод.

Температура поверхности нагрева

Расчет температуры поверхности нагрева можно было бы сделать по уравнениям (32) — (35) или (41) — (44). Но для этого необходимо знать количество тепла, передаваемое на рас­сматриваемом участке. Особенно хорошее представление об этом дает следующее соотношение:

^г. пов _ ав (479)

^в. пов ^в аг

В этом уравнении £г. пов°С— температура более нагретой по­верхности, /в. пов — температура более холодной поверхности. Уравнение (479) выражает общий закон, распространяющийся на плоские или тонкие стенки: температурные перепады /г — ^Г. ПОВ И ^в. пов обратно пропорциональны коэффициентам

Теплоотдачи.

Температура поверхности яагрева на более горячей стороне в случае плоских стенок

/р. пов = аг~*г + ав'<в + ав - Д^пов оС (480)

Аг 4" яв

И на более холодной стороне

£ __ аг • Ч~ ав ’ аг • А ^пов о£ (481)

А + ав

В этих уравнениях Л/Пов — разность температур /г. пов— ^в. пов, наблюдаемая на обеих сторонах поверхности нагрева. Если ее

5

Выразить через тепловое сопротивление —то темиаратура по-

А

Верх« ости на более горшей' стороне будет, равна

ССр ' ^

Аг * ’Ь °В ‘ "Ь Г *

^г. пов =----------------------------- ■---------------- *---------- °с (482)

Аг • ав • в

«г + «в +------------------------------------------

А

И «а более холодной стороне

ССр ^ ССр • 5 ®г • ав • ^в Г ■

/в. псв =--------------------------------------------------------------------------- °С. (483)

Аг • ов • 5 «г + “в + ^

Для многослойных плоских стенок в — вся толщина стенки, К —

Эквивалентный коэффициент теплопроводности по уравнению

£

(25). Если тепловым сопротивлением —можно пренебречь по сравнению с сопротивлением теплоотдачи —, то температура

Поверхности при 5 = 0 или X = оо

4 4- аГ * + ав * ^в ог (ДЪД.

*г. пов — *в. пов — ; (4о4)

Аг + ав

Для стен с любым тепловым сопротивлением это будет средняя температура стенки. Для стенки трубы справедливо соотноше­ние

Tг ^Г. ПОВ ав ' Рв (485)

^в. пов — ^в «г.^г

Здесь — поверхность более горячей стороны, ж2; — поверх­

Ность холодной стороны, мг.

Температура более нагретой стороны

®г * Рг ’ ®в * Рв ' 5 • /р

TOC o "1-5" h z аГ * 4* ав * ^В * ^В + ' * р

^г. пов= ---------------------------------------------------------------------------------------------------- Vе °С - (486>

Г I с I аг * • ав • Рв • 5

Аг • 4' аВ • ^в 4" * с

Л * /*ср

Здесь — теплапередающая (поверхность, взятая в середине между обеими 'поверхностями; следовательно, в случае полого цилиндра

TOC o "1-5" h z Р _ м*

Ср 2 -*1 •

Температура более холодной поверхности

&Г ‘ рг ' ' Рв ’ ® * ^в

Аг‘^г*^г4“ав*^в*^в4““ - г

^в. пов = ------------------------------------------------------------- _ ;Р-------------------------------- °с. (487)

Г - , г - ,* аг ' Рг ' аВ ‘ Рв ' Б аГ ' Рг ав ’ Рв 1 с

А. гср

Если стенка трубы многослойная, то вместо А, нужно подстав­лять эквивалентный коэффициент теплопроводности А, ср, опре­деляемый по уравнению (26).

Вывод формул

Прежде всего рассмотрим наиболее важный технический случай: тепло­обменник, работающий по принципу противотока (см. рис. 50).

Количество тепла, передаваемое на бесконечно малый элемент поверхно­сти, равно

ЙО, = И • с1 • Рх • (/г — tв) ккал/час. (488)

Количество переданного тепла должно равняться увеличению или уменьше­нию теплосодержания протекающей среды. Если температура более нагретой среды после прохождения элемента поверхности нагрева йРх снизится на <И °С, то количество отданного тепла [обозначения, как и в уравнении (196)1

= — Ц7Г. сНг ккал/час. (489)

Уменьшение теплосодержания более холодной среды в том же месте

— — №в • Лв ккал/час. (490)

Отрицательные знаки объясняются тем, что в положительном направлении потока, т. е. в направлении движения теплоотдающей среды (по рис. 50 слева направо) во всех случаях появляется уменьшение температуры, по­этому (Ит и сНв отрицательны.

Из уравнений (489) и (490)

Если нижнее уравнение вычесть из верхнего, то получим

(491)

«(■гг-тгг)- ,492)

Подставляя й(} из уравнения (488), получим

(493)

(I (/г? в) = к • йРх • (/г /в) ^ ^ — 1^™")*

:(«^г й^в)

Интегрирование этого уравнения после деления обеих частей на £г—^в дает выражение:

ІП (*г ^в)— к - Рх — 1+С. (494)

Здесь м2 — поверхность нагрева, которая »омывается более нагретой сре­дой, начиная от входа до точки, темшература которой Постоянная интегри­рования С определяется из таких граничных условий, чтобы для начала по­верхности нагрева (Р0) разность температур /г — tв была заменена

Значением ^г1—* в2 (см. рис. 50), следовательно, по уравнению (494)

1п(/п-'в2) = С. (495)

Подставляя уравнение (495) в уравнение (494), получаем

,496’

Если через Т7 обозначить общую поверхность нагрева, то для Рх — Р раз­ность температур — tв по рис. 50 перейдет в tг2— *вь и уравнение (496) примет вид

"-£йг—(,97)

Среднюю разность между температурами обеих сред А/Ср можно определить следующим образом. Найдя коэффициент теплопередачи, получим

TOC o "1-5" h z (2 = к-Р - Д/ср (498)

Или

К. ^ . (499)

А /ср

Если заменить кБ в уравнении (497) его значением, полученным из уравне­ния (499), то будем иметь:

(500)

. ^Г2 ----------- ^В1________ С / 1 1

^Г1 -- ^В2 А ^ср /

И/п

А/ср =------- ^. (501)

1п 2 В1

(502

И

(503)

(504)

(505)

Если оба эти выражения подставить в уравнение (501), то получим искомое уравнение (448).

Температура среды по участкам и на выходе определяется ^следующим образом.

Потенцируя уравнение (496), получим

(506)

Следовательно, разность температур в любой точке потока

/г tB — (^гі — ^вг) * ^ С* (507)

Согласно рис. 50 количество тепла, отдаваемое более нагретой средой,

(508)

Q = Wr (trl — tr) ккал/час

И количество тепла, воспринятое более холодной средой в интервале тем­ператур,

(509)

Q = WB • (tB2 — tB) ккал/час.

Так как <2 в уравнениях (508) и (509) должны быть равны, то, приравнивая правые части уравнений и решая относительно /в, получим

(510)

Если это значение tB подставить в уравнение (507), то получим

W р

(511)

= ^в2 — (^гі ►г) + (*гі — ^вг) * е

W в

После решения относительно tr

SHAPE \* MERGEFORMAT

•

О.

C. (512)

TB2 Wr • tri ~4~ ^в (^n — ^вг) e

WB — Wr

В этом уравнении температура более холодной среды на выходе /В2 не из­вестна. При ее определении необходимо учесть, что / в конце поверхности

Нагрева, т. е. для Т7* = Т7, переходит в температуру на выходе, так что урав­нение (512) преобразуется в выражение

•

(513)

*В2-^Г*'п+^В (/п-*В.)-в

Это уравнение содержит две неизвестные величины: температуры /г2 и /в2 на выходе; но они связаны одно с другим уравнениями (502) и (503); если приравнять эти уравнения, то получим

(514)

(^п — ^гг) — ^в (^в2 — ^ві)

И, следовательно,

(515)

(^В2 ?В1)-

Если это значение 1Г2 подставить в уравнение (513) и решить его относитель­но единственной оставшейся неизвестной величины tB2, то получим

Г - к-в(------- Ц

I ХР ХР )

°С. (516)

Іві(УГл-Гг) + Рг. іг111-е_________ г в ].

К • Р

Все величины, входящие в правую часть этого уравнения, известны. Преоб-

Разуем ее так, чтобы получить критерий с образованием двух групп

И'в

Переменных, т. е. чтобы практически правая часть уравнения (516) зависела лишь от двух переменных. Если для дальнейшего упрощения в числитель прибавить выражение +^п — ^гъ то получим искомое уравнение (455). Тем­пература в любой точке движущегося потока определяется из уравнений (512) и (516). Если 1В2, определенную из уравнения (516), подставить в урав­нение (512), то получим искомое уравнение (457), по которому определяется температура в любой точке теплоотдающей среды. Если в уравнение (510) подставить найденное значение ^г, то найдем температуру тепловосприни­мающей среды. Получим, таким образом, уравнение (458). Конечная температура (Г2 более нагретой среды получается либо подстановкой в уравнение (457) значения =/ либо подстановкой в уравнение (515) зна­чения tВ2, полученного из уравнения (516). В этом случае приходим к урав­нению (454). Количество передаваемого тепла можно определить из урав­нений (502) и (503) и, подставляя значения *Г2 или ^В2» получить уравнения (460) и (461). Особенно просты будут уравнения, если водяное число одной из движущихся сред бесконечно большое, в результате чего температура данной среды не изменяется ни во времени, ни в пространстве. Этот случай наблюдается, например, в паровых котлах, где температура воды остается постоянной в любой точке среды.

Чтобы выразить предельный случай, когда ИР-м», уравнение (460) необ­ходимо преобразовать так, чтобы числитель и знаменатель были умножены на

Гв

. Тогда уравнение преобразуется следующим образом:

W г

■

— к 1 — е

F (—---------- Ц

V

(517)

Wr wj

-k F (—--------------- Ц

I Wj

IrT-e

-k-p(—-------- — wr wR)

K-F

Гв I WT WB ) wb.

Для Wr =oo будет *=0 и e = e

W r

Следовательно, для Гв= oo из уравнения (517) получим

L.^)

Q = (/г1 - tBl) - (518)

^в

— е

Или

K. F

А = ((Г1-1в1)Гъ\-е в /. (519)

То же самое уравнение можно было бы получить проще из формулы (459) для прямотока с Гв =°°, причем вместо Гв ввести Гг. Совпадение обоих уравнений объясняется тем, что при теплопередаче к среде, характеризуемой одинаковой температурой в любой точке, нет никакого различия между пря­мотоком и противотоком.

Неопределенные формы, в которые переходят уравнения (454), (455),

Гг

(460), (475) при —— =1, можно преобразовать путем раскрытия этих неоп-

► Иг з

Ределенностей, дифференцируя числитель и знаменатель в определенные.

Гг

В качестве примера приведем уравнение (475), которое при =1 дает не

" в

1-е-°

Определенную форму:

*Ппрот =

, — 1 •е~° О

Для раскрытия этой неопределенности необходимо предположить, что

Гг

Гг=const и лишь Гв изменяется таким образом, что отношение — =х при-

W в

Гг

Ближается к 1. Если —- = х, то w в

К • Р

Л

К • Р

TOC o "1-5" h z 1Г(1-Х'е >

« р - гг"-я

(520)

»■г '*

К • ^ кР

(I - *> — —- (1 — ж)

К • ^ . «"г

• - в — в

При * =* 1 из этого уравнения получим определенную формулу кР

1

Или

*•' •. 1 ' г-

' к. /?

Так как при х=1 —----------- = 1, то, следовательно, пв#уравнению (475)

**мин

^прот = ~ » (521)

1+-ГГ

Т. е. находим искомое уравнение (477).

Чтобы выразить температуры на выходе через коэффициент полезного действия, надо связать соотношения

Q = (?макс * 7)»

(} = №г * (^п ^гг) или О.—^ъ' Увъ *в1)

И

TOC o "1-5" h z Смаке == ^мин (^п ^В1)•

Тогда получим температуру теплоотдающей среды на выходе

*г. = <п - (<п - « • Ч (522)

И' Г

И температуру тепловоспринимающей среды на выходе

^В2 = ^В1 + ^ (^Г1 ^В1) • ■*) °с. (523)

Для прямотока примененный вывод остается почти неизменным. Уравне­ние (490) меняет свой знак, так как с движением в направлении к поверх­ности нагрева растет температура /в» следовательно, величина Лв будет положительной.

Таким образом, вместо уравнения (492) получим выражение

(1Г+п') (52,)

21 А. Шах

И вместо уравнения (494)

Ln«r-/B)--fc. F,(-^ + ~-)+C. (525)

Постоянная интегрирования С определяется здесь из условия, что при Fx — О температурные разности tг— *в и tri— ^bi должны быть равны. Тогда

Ln(/n-*Bi) = C (526)

И уравнение (525) преобразуется в выражение

При Fx — F разность tr—*в будет равна разности конечных температур tT2 —

— ^в2 (см. рис. 49); с учетом этого уравнение (527) примет вид

,528)

Q

Если подставить вместо k-F, согласно уравнению (499)------------------- , то получим

А /Ср

JL + JL

TOC o "1-5" h z А --------- ------- ~‘t----- • (529>

__ jn *Г2 *В2

TTi /В1

Теперь уравнения (504) и (505) справедливы также для прямотока

Wr П Г*

И <•

М <м*

Следовательно,

AfcpSaA».rJ«.+.r«--^ (530)

Гг1 --- *В1

1п,

*Г2 *В2

Это уравнение идентично уравнению (447). Однако надо учитывать, что

. *г2 ^в2 . , — ^В1

__ jn-------------- = _|_ 1п-----------

. _ ~ ^В2

Натуральный логарифм 1п преобразуется в десятичный ^ путем умножения на 2,303.

Температуры на выходе при прямотоке получаются потенцированием уравнения (527):

-

*wr wB)

K

Tr-- ______

T'X-tbi~e ■ (531)

Количество тепла, воспринимаемое до точки Рх (см. рис. 49), в прямоточном теплообменнике

С? = (/в — ^ В1)

И количество тепла, отдаваемое более нагретой средой,

Ф = и? г — /г).

Приравнивая правые части этих уравнений, получим

Ц7_

TOC o "1-5" h z + (532)

И

Ц7п

= /Г1 ш • (^в — ^вг)- (533)

Ч

Если подставить /в из уравнения (532) в уравнение (531), то получим тем­пературу в любой точке теплоотдающей среды (в пересчете на /**):

■к Рх + —!—1

1ГГ >

---------------------------- .. (534)

Гг

1 + ¥Г

Это уравнение показывает, как изменяется величина / с увеличением поверх­ности нагрева /*г» начиная от входа теплоотдающей среды до данной точки. Легко определяется и конечная температура tт—tт% при условии Уравнение (534) преобразуем в более удобную для некоторых целей формулу (452)

К рх (-І - - Ь —)

'и. и, /

^В-/В1 + ^Г-<Г1+^В (*Г1 —^Ві) • в

; (534а)

■ /„ + И? г • + ^в • ІГ1 - ^в • *п +.

Х И - гв)

(5346)

+ 0^в(^Г1 ^ві) ' е

Это уравнение после вынесения за скобки ^пО^г+^в) и последующего преобразования дает искомое уравнение (452).

Температура тепловоспринимающей среды определяется из уравнения (531), в которое подставляем значение t по уравнению (533), а в остальном поступаем так же, как и при расчете *г.

Температура поверхности нагрева определяется следующим образом. Количество тепла, передаваемое на более нагретой стороне,

Я = “г (*Г — 'г. нов) ккал/м2 час;

На более холодной стороне

Я = “в (*в. пов “ *В) ккал! м* • час-

Поэтому

Аг (^г ^г. пов) ав ^в. пов (535)

Из этого уравнения непосредственно следует уравнение (479).

Если принять, что *г. пов — *в. пов == А *пов.

^г. пов ^в#пов “ ^ ^пов (536)

И сообразно с эггим за(менить ^в. пов (в уравнении (535), то после пересчета на *г. пов получим уравнение (480). Если заменить /г. повна /в. повС помощью А/Пов, то получим уравнение (481). Но температурный перепад ЛпоВ—^в. пов=Л*пов в большинстве случаев неизвестен. Его можно определить по закону тепло­проводности. Сообразно с этим, согласно уравнению (2а),

X

<7 = — • А /Пов * кал/м? • час.

Приравнивая количество подведенного тепла <7 к количеству переданного теп­лопроводностью тепла <7, получим

X

АГ (^Г ^Г. пов) == 5 (^Г. ПОВ ^в. пов)* (537)

Решая это уравнение относительно /в. пов и подставляя найденную величину в уравнение (535), получим

[

АГ • я ^ ч *|

^г. пов ^ ^г. пов) ^в I •

Решение этого уравнения относительно /г. пов дает искомую температуру по - верхности нагрева ^г. пов [см. уравнение (482)]. Другую температуру можно опрёделить, если уравнение (537) решить относительно tг. П0B и эту величину подставить в уравнение (535).

Если речь идет о стенке трубы, то количество тепла, передаваемое на более нагретую поверхность Т7,

<2 = “г РГ ■ (‘г — 'г. пов) ккал/час

И количество тепла, отданное холодной поверхностью,

<2 = “в • • ('в. пов — *в> ккал/час.

Приравняв (правые части этих уравнений, /получим

Аг ' ^ (*г ^г. пов) “ ав * * (^в. пов ^в)* (538)

Из этого равенства находим уравнение (485).

Тепло, проводимое стенкой трубы по уравнению (22), равно:

_ ^г. пов ^в. пов

Ь/Чр.

Или

Л ^ ‘ ^ср (^Г. ПОВ ^в. пов)

5 =------------------------------------ ккал/час.

Приравнивая правые части этих уравнений, получим

„ .. . ч ^ * ^ср (^Г. ПОВ ^в. пов)

Аг • (*г - *г. пов) = ------------------------- -------------------- ;

Из этого равенства находим температуру

T - t - 5 ' “Г ' Fr (<г ~~ ^г. пов)'

*В. ПОВ *Г. ПОВ - V С •

Л • гср

Если это /впов подсггавить в уравнение (538) и решить уравнение относитель­но tr. лов. то получим уравнение (486). Для расчета *в. пов необходимо коли - чество тепла, проведенного через стенку, приравнять к количеству тепла, от­веденного от нее, с целью исключения величины /г. пов; следовательно,

„ v * * ^ср (*г. пов ■— *в. пов) /г. ллч

“в • FB • ('в. пов - 'в) = -------------------------------- ------------------------ •------------------------ (540)

Это уравнение надо решить относительно /г и из полученного уравнения под­ставить в уравнение (538) величину ^г. пов. После »того, «решив относитель­

Но *в. пов, іполуїчим уравнение

П л, ^ * ^ср л, ав^в 9 ^ * Fcp * ^в

«bJVb Н /г +---------------------

S Ctp • fp • s

Vno. = ------------------- Г7--------------- —--у Гх , °С. (541)

Г« , * ^Ср аВ • Гв Л * ^Ср

Ав-ГвН----- * --------------------- —+

Ar>FrS

Если числитель и знаменатель умножить на величину - г——, то получим ис-

A-Fcp

Комое уравнение (487).

Б. Перекрестный ток.

Принцип перекрестного така схематически изображен на рис. 54. Среда с водяным числом WB ккал/час-°С и равномерной температурой на входе t0 движется в направлении, перпендику­лярном трубному пуч1ку, который состоит из п параллельных радов труб. По трубам движется »среда с водяным числом Wr и температурой на входе t °С. Общая поверхность нагрева сос­тавляет F м2, следовательно, поверхность одного ряда труб

Р

— м2. Количество среды, протекающей по одному ряду труб,

W

Характеризуется водяным числом, равным —— ккал/час°С. Точ-

П

Ный расчет теплообменника, работающего по принципу пере­крестного тока, значительно сложнее, чем расчет прямоточного или противоточного теплообменника. Для такого расчета, как и для всех теплообменников, основной формулой служит

Q = k • F ■ Д /ср ккал/час. (542)

Здесь средняя разность температур приблизительно равна

Ai *1 — ^0 + ^2—ton /K/IQ4

А*,

МШШшаттатшЖУ fҐп І »

МШ П

Лм2 'ПМ   Fa *01   Т   '

И

*2] *22 *23 *ф-0 I

*Ип-г) Wc

Щ Ta

Рис. 54. Схема рекуператора, ра­ботающего по принципу пере­крестных потоков

В этом уравнении ti и (0 температуры на входе; tim и ton— средние температуры на выходе (ton равна температуре нагрева­емого потока и t2— температура «отходящего газа»). Величи­ну Д/ср можно получить несколько точнее, если перекрестный ток представить как нечто среднее между противотоком и пря­мотоком, зная соответственно средние значения At ср для прямотока и противотока [по уравнениям (447) и (448)]. На практике перекрестные пото­ки часто образуются так, что одна среда протекает зигзагообразно на­встречу другой. В этом случае мож­но применить непосредственно фор­мулы, выведенные для противоточ - ных теплообменников. Подробный расчет теплообменника, работающе­го по схеме перекрестных потоков, можно вести следующим образом. Через один ряд труб за час про­текает среда с водяным числом Гг Ккал/час °С. Температура вне­шней среды с водяным числом WB изменяется при омывании каж­дого ряда труб. По рис. 54 сред­няя температура после прохожде­ния первого ряда составляет t0ь по­сле прохождения второго ряда труб Ton, после n-ного ряда труб (пп °С. Температура среды с водяным числом WT на выходе из первого Ряда труб составляет t2ь из второго t22, из n-ного t2n°С. Количество тепла, передаваемое в теплообменнике с пере­крестными потоками, составляет Qi = (^о — ton) ккал/час. (544) Средняя температура среды, протекающей по трубам и характе­ Ризуемой водяным числом Wr на выходе Tin = ^+/м + Л».+ у.- + /«я »с. (545) П Количество тепла, отданное или воспринятое при этом, равно: Q2 = №г (t2 — ii) ккал/час. (546) Так как здесь не учтены 'внешние тепловые потери, то Qi = Q2- Температуры на 'выходе, необходимые для расчета, можно выра-

Зить с помощью единых формул; эту операцию проделал В. Нус - сельт[183]. На так как эти формулы очень сложны и трудно приме­нимы в практических расчетах, то кажется более выгодным вести расчет для каждого ряда труб в отдельности. Температура среды, протекающей через первый ряд труб, с водяным числом

TV7

—- ккал! час-°С на выходе п

_ kF

TOC o "1-5" h z tn = h + (h-t,)-e W* °с. (547)

Средняя температура среды, характеризуемой водяным числом WB и протекающей топерек первого ряда труб, равна:

КР

Ш W

^ = + i}-e г)°с. (548)

П • W в

Тт ^ г » «

Для среды с водяным числом —, протекающей через второй рйд

П

Труб, темотзратура на выходе равна

K-F

^22 = А>1 + (Яi + ^oi) * е г °С. (549)

Здесь toi определяется из уравнения (548). Средняя температура среды, протекающей перпендикулярно к трубам между вторым и третьим рядом,

KP

= Гг)°с. (550)

П ■ W и

Здесь ^oi также определяется из уравнения (548). Температура среды, протекающей по третьему ряду труб, на выходе

1 _ k-F

W

*23 = *02 + {к-1п).е г °С. (551)

Величина toi определяется из уравнения (550). Ведя с такой последовательностью расчет температур, доходам до п-ного ряда труб. Температура среды, протекающей по последнему

Ряду труб и имеющей водяное число—, на выходе из теплооо-

П

Менника

_ k-F '

W

Hn =^о(л - 1) + (t—(л — 1)) * £ г °с. (552)

Температура среды, вытекающей из теплообменника перпенди­кулярно трубам, равна

K-p

VV7 Ш

Ton = t0(n-n — (to(n-i)-ti)- -Ц - -(1—е Г)°С. (553)

Я • WB

В этих уравнениях »величина to (П— i> известна из расчета пред­последнего ряда труб. Для расчета количества тепла, передава­емого всем трубам или отдельному ряду, достаточно уравнений (544), (548), (550) и (553), т. е. достаточно расчета температур­ной кривой среды, протекающей перпендикулярно трубам. Средняя температура среды протекающей по трубам,

Может быть определена не по уравнению (545), а проще, из сравнения правых частей уравнений (544) и (546):

*2m = *i+-^--(*o-0°C, (554)

ГДе ton определяется из уравнения (553).

Вывод

Первый ряд труб омывается <арадой с постоянной в любой точке темпера­турой. Поэтому водяное число среды Wв лю отношению к количеству тепла, воспринимаемому средой с водяным числом Wr, можно рассматривать как бесконечно большое, что обеопечивает применение уравнения (468). Сообразно с этам температура ар еды, протекающей по первому ряду труб, на выходе

K • F

К 1 = 'о + (*1 —<о) • е Wr °с. ' (555)

F

Поверхность нагрева одного ряда труб равна — м2, а протекающая по этому

Wr

Ряду среда характеризуется водяным числом — ккал/час • °С. Следовательно,

П

Показатель степени в уравнении (468) будет (равен

------------ или ----------- .

W г W г

В дальнейшем мы предполагаем, что температура и больше температуры /о; следовательно, три движении фвды с водяным числом Гг >по трубе темпе­ратура среды уменьшается. Сейчас необходимо условиться о знаке и придер­живаться его во всех исследованиях. Выведенные формулы справедливы так­же и для случая, когда /1 < /о-

РГ

Количество тепла, воспринимаемое средой----------- при ее движении по пе-р-

П

Вшу ряду труб, можно найти после определения (водяного числа

1ГГ

Рх =------- • (/21 — *1) ккал/час. (556)

Количество тепла, отдаваемое средой с водяным числом W', протекающей перпендикулярно первому (ряду труб:

Qi = (t01 — /0) ккал/час. (557)

Так как коліичество воспринятого тепла должно (быть равно отданному, то из. уравнений (556) и (577) следует

П

Подставляя значение fei, найденное из уравнения (555), іполучим:

-‘і',

WB (toi - Іо) = — lh - to - (h - t0)-e Tl

Оl

Решаем это уравнение относительно

K • F

ЭД7 W

Toi = t0 + —r^—.l(t1-t0)-(t1-t0).e rJ.

N • WB

Получаем, таким образоїм, искомое уравнение (548).

Соответствующие температуры во втором ряду труб 'можно определить аналогичным образом, только вместо t0 надо подставить температуру tou Это единственное, чем отличаются условия во втором ряду от условий пер­вого ряда. Соответственно в третьем ряду труб нужно подставлять tQ2 вмес­то toi и т. д. При таком методе расчета не учитываются два важных обстоя­тельства, но их влияния взаимно компенсируются. Первая ошибка заключает­ся в том, что 'расчет велся но средним постоянным температурам /ou to2 В действительности температура среды WB после прохождения по­

Перек первого ряда труб не остается постоянной вдоль трубы, а уменьшается от верха трубы к низу. Так как температура среды Wг, протекающей в тру­бах, уменьшается от верха к низу, то разность температур между средами Wv и WQ от верха трубы к низу возрастает. Поэтому тепловоаприятие сре­ды W* в верхней половине первого ряда труб будет больше, чем в нижней; следовательно, среда Wr, омывающая ряд труб їв верхнем конце теплообмен­ника должна быть более горячей, чем в нижнем. Эта разница должна сказы­ваться тем больше, чем больше рядов труб омывает среда Wв. Но в выше­приведенных выводах вместо этого распределения температур приняты сред­ние постоянные температуры toi, t02... Таким образом, расчет как бы создает менее благоприятные условия для теплопередачи, чем в действитель­ности. Так как температура среды WB мала там, где другая среда имеет так­же низкую температуру, а аналогично высока там, ігде в другой среде тем­пература высокая, то эти условия соответствуют принципу противотока (рис. 50), который характеризуется более высокой теплопередачей по срав­нению с друг и м»и схемами теплообменников. Следовательно, принимал тём - пературу среды WB постоянной по длине трубы, получаем заниженную теп­лопередачу. '

Вторая ошибка, которая была сделана в вышеприведенных выводах, за­ключается їв пренебрежении (изменением температуры среды WB тгри про­хождении через каждый ряд труб. В действительности среда Wв приходит, например, в первый ряд труб с температурой t0 и 'покидает его с температу­рой foi. Следовательно, точнее было бы вести расчет с более высокой тем­пературой —0 ^ —вместо t0. Чтобы не усложнять расчет, мы этою не делаем* и получаем завышенную величину теплопередачи.

Следовательно, обе ошибки взаимно компенсируются и ими. можно пол­ностью пренебречь, так как, кроме всего прочего, в абсолютном выражении они не очень велики.