Для термодинамического рассмотрения необходимо знать вы­ражение для работы рассматриваемой системы против внешних сил. В общем случае, когда деформируемое тело имеет произволь­ную форму, работа системы против внешних сил

ЬА= — { —dnds,

J ds (s)

где dF — элементарная внешняя сила, приложенная к элементу поверхности ds, и dn — элементарный путь перемещения элемента поверхности вдоль нормали к поверхности.

Для термодинамического анализа высокоэластичности достаточ­но рассмотреть, однако, более простой случай — однородную де­
формацию кубика единичной массы вдоль осей координат, парал­лельных ребрам кубика. Единица массы выбирается произвольно.

Обозначим три оси координат индексами 1, 2, 3. Нормально к граням кубика приложены растягивающие (или сжимающие) си - гЛы Fb F2, F3 (рис. 3.4). В деформированном состоянии площади граней единичного кубика обозначим su s2, s3, а в недеформирован - ном — so. Нормаль направлена от поверхности наружу. Если внеш­ние силы Fi направлены по нормали (силы растяжения), то они

Рис. 3.3 Рис. 3.4

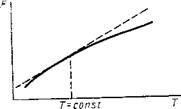
Рис. 3.3. Зависимость равновесной силы F резины в растянутом состоянии от температуры при заданной длине L>L0, где L0 — длина образца резины до растяжения

Рис. 3.4. Образец резины в виде единичного кубика, подвергнутый действию растягивающих сил

считаются положительными. Обозначая нормальные напряжения ;Oi' = Fi/Si, где i— 1, 2, 3, получим для работы вместо прежнего вы­ражения

з

ЬА = — ^ a'isi • 2 dtir

i=l

Пусть из трех компонентов напряженного состояния наименьшим по абсолютному значению является (Тз7. Введем новые значения на­ряжений оь СГ2, сгз таким образом, чтобы 01 = о/+<вз'- Очевидно, = —р, где р — всестороннее внешнее давление, положительное. огда, когда оно направлено против нормали (всестороннее сжатие), отрицательное в противоположном случае (всестороннее растяже­ние). Обозначая удлинения dLi = 2drii, получим 6А = —2(а«—p)sidLi “ли, учитывая, что оз^О и! lSidLi = dV, имеем

bA=pdV — — 32s2dZ,2. (3.18)

Полученная формула применима как для твердых, так и для вы- ‘окозластических тел, однако физическая природа всех ее членов динакова лишь в первом случае. Для резины только первый член, ыражающий работу против сил всестороннего сжатия, имеет при*

роду деформации, характерную для твердых тел. Последующие же два члена обусловлены совершенно иной, высокоэластической при­родой деформации, связанной с перегруппировкой и ориентацией звеньев цепных молекул. В случаях, если образец имеет форму полоски, для которой грани параллелепипеда в недеформирован - ном состоянии есть х0ь ^02, £оз, пользуются условным напряжением ft = Fi/so. Формула для работы примет вид

ЬА =pdV — fxSoidLi — /з^оЖг - (3.19)

Для твердых тел вследствие, малости упругих деформаций обычно не различают истинные и условные напряжения, так как so/* Для резины эти величины смешивать нельзя.

Из выражений (3.18) и (3.19) следует,* что трехмернаД дефор­мация полимера в рассмотренном случае сводится к объемной уп­ругой и двухмерной высокоэластической. Однако термодинамиче­ское рассмотрение двухмерной высокоэластической деформации резины не внесет ничего принципиально нового по сравнению с рассмотрением более простого случая — одномерной высокоэласти- ческой деформации. Поэтому далее термодинамический анализ ПР°~ водится для одномерной деформации резины, для которой формула (3.19) примет следующий вид:

bA = pdV-FdJL, (3.20)

где р — давление внешней среды; F = Sof — внешняя сила; услов­ное растягивающее напряжение; L — длина образца резинь* в про­цессе деформации.

Одномерное деформированное состояние данного конкретного образца резины можно характеризовать однозначно как парамет­рами F, L, так и обобщенными параметрами f, Я, где / — условное напряжение, а Я = 1 + е — кратность растяжения (относительная длина). Однако деформированное состояние резины как материа­ла однозначно нельзя характеризовать величинами F, L из-за влия­ния на L теплового расширения резины. Поэтому в дальнейшем бу­дут применены параметры f, Я, однозначно описывающие деформи­рованное высокоэластическое состояние резины. В термодинамике газа, как известно, вместо F, L применяются также обобщенные силы и путь, в данном случае имеющие вид р и V. Из этих двух па­раметров независимым является один.

В анализе, приводимом ниже, в качестве независимого пара­метра принимается деформация X. Кроме деформации X состояние резины определяется еще температурой Т и всесторонним давле­нием р. Эти три независимых параметра полностью определяют равновесное состояние резины, подвергнутой одномерной деформа­ции растяжения — сжатия.

Выразим формулу (3.20) в параметрах /, Я. В случае одномер­ной деформации Я = L/L0, где L0 — длина образца (или рассматри­ваемой части его) в недеформированном состоянии, зависящая от давления и температуры. Отсюда следует, что dL = LQdXd-XdLo,

Учитывая также, что F = s0f и VQ = s0Lo, где Vq — удельный объем в недеформированном состоянии, получим

ЬА = pdV - V0fdk - VJla&T + VQf)Mp, (3.21)

где температурный коэффициент линейного расширения « = = L0-1(dLoldT)p и коэффициент «линейного» сжатия к = =—Lo~l (дЬ0/др)т относятся к недеформированному состоянию (Х = 1). Поэтому а и к есть константы, не зависящие от X (коэффи­циент объемного сжатия К^ок).