ПСЕВДОРАЗЖИЖЕНИЕ (ТИКСОТРОПИЯ) ЦЕМЕНТНОГО ГЕЛЯ
 19 декабря, 2012
19 декабря, 2012  admin
admin Свойство многих структурированных систем разжижаться под влиянием механических (динамических) воздействий широко используют в различных технологических процессах. Согласно представлениям, изложенным в работе [107], концентрированный гель, содержащий
Огромное количество сцепленных Частиц, может бьиъ путем механического воздействия приведен в такое неупорядоченное состояние, что все частицы окажутся в оживленном броуновском движении; в связи с этим гель переходит в псевдожидкое состояние — золь. По прекращении механического воздействия наступает обратный процесс — золь снова превращается в гель, но с более ориентированными и прочными структурными связями. По установившемуся мнению, количество жидкости, при котором возможен обратимый переход «гель^золь», должно быть достаточным, чтобы частицы имели возможность совершать броуновское (тепловое) движение.
Типичным упруго-пластично-вязким телом, обладающим обратимыми тиксотропными свойствами в стадии формирования коагуляционной структуры, является цементный гель при значениях X от 0,876 до 1,65 (в гомогенном состоянии—до 2). Как было показано, изменение реологических параметров то и ir с увеличением скорости деформации сдвига связано непосредственно с явлением обратимой тиксотропии цементного геля. Это свойство широко используют при многих методах обработки смеси как на стадии приготовления, так и при формовании изделий.
Для псевдоразжижения цементного геля в указанных пределах требуются различные по интенсивности механические (динамические) воздействия. Чем меньше X, прочнее коагуляционная структура, тем выше должна быть частота вынужденных колебаний. При этом амплитуда их может быть как угодно малой, так как абсолютная величина деформаций, вызывающих разрушение структурных связей и взаимные перемещения частиц, соизмерима с радиусом действия ван-дер-ваальсовых сил. При Х=0,876 тиксотропные превращения провоцируются в диапазоне частот вынуждаемых колебаний 150—200 Гц, а при 1,65 система разжижается от малейшего встряхивания. В начале схватывания цементного геля (по Вика), когда вся капельная жидкость находится в связанном состоянии [141], цементный гель может быть тиксотропно разжижен (как и при Аг=0,876) только при частоте вибрирования порядка 200 Гц.
Коль скоро псевдоразжижение цементного геля при каждом значении X, определяющем расстояние между частицами, достигается под влиянием соответствующей
частоты вынужденных колебаний, можно предполагать, что в основе механизма обратимой тиксотропни гелей лежит явление резонанса, наступающего при близком совпадении частот вынужденных колебаний с частотами собственных колебаний сольватированных частиц твердой фазы. Отсюда следует, что механизм проявления обратимой тиксотропии цементного геля, обусловленный нарушением ван-дер-ваальсового взаимодействия между частицами цемента, нельзя интерпретировать, как это обычно практикуется, при помощи теоретического аппарата динамики стержневых систем. Физически более обоснованы представления об изменении сил взаимодействия между атомами трехмерных кристаллов.
Большинство соединений, составляющих цементные частицы, относится к классу ионных кристаллов. Они могут иметь соответствующую химическую формулу, и в этом смысле представлять собой единую фазу в многокомпонентных смесях. С другой стороны, в таких кристаллах возможны вариации состава, о чем, например, свидетельствует целая серия алюмоферритов, описываемых формулой А1203Ре03(/г—1). В этих случаях ионные кристаллы могут отклоняться от стехиометрическо - го состава так же, как и металлические, твердые растворы. Для простоты рассмотрим лишь соединения из двух элементов одного стехиометрического состава.
В идеальной решетке таких кристаллов атомы должны занимать определенное место, и тем не менее ни один поликристалл не является абсолютно жестким, так как его можно деформировать под действием сил конечной величины. Тогда, затратив определенную работу, можно сместить атомы с их места на вполне определенное расстояние х.
Несмотря на то, что такое неоднородное твердое тело, как цементная частица, состоит из большого числа химических элементов, образующих сложные соединения, качественная картина природы сил взаимодействия от этого не изменяется.
Согласно современным исследованиям [38, 69, 85, 121], межатомные силы притяжения в твердом теле проявляются на таких расстояниях между атомами, когда силы отталкивания еще не действуют. Обе эти силы возрастают с уменьшением расстояния между атомами, однако силы притяжения проявляются по мере их сближения медленнее, чем силы отталкивания.
7*
Если г — расстояние между атомами; т — постоянная, зависящая от физической природы сил притяжения, то при некоторой постоянной величине В взаимодействие между двумя смежными атомами выражается отношением
FNP = -B/Rm+1. (2.43)
В свою очередь, если А и п — константы для данного кристалла, изменение сил отталкивания от расстояния определяется следующей приблизительной формулой:
F0TT = Л//*^-1. (2.44)
Поскольку с уменьшением г силы отталкивания возрастают быстрее сил притяжения, должно соблюдаться условие тСп. Результирующая двух этих сил определяется уравнением
F = F0TT + Fnp = СA/rn+l) - (в/г**1). (2.45)
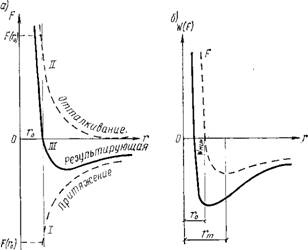
Графическая интерпретация сил взаимодействия между атомами и более крупными частицами в функции расстояния между ними приведена на рис. 2.18, а, где по оси абсцисс отложено расстояние между смежными атомами, а по оси ординат — силы взаимодействия между ними: I и II — силы притяжения и отталкивания соответственно и III — результирующая двух этих сил. Атомы могут находиться в равновесных положениях, если соблюдается равенство сил притяжения и отталкивания, и в этом случае потенциальная энергия твердого
Тела должна быть минимальной. Полагая, что F=—— ,
Dr
Найдем, что суммарная потенциальная энергия взаимодействия двух атомов выражается зависимостью
W =■• (А/пгп+1) — (В! тгт+1). (2.46)
На рис. 2.18,6 показано изменение потенциальной энергии атома в функции от расстояния между ними в твердом теле. При значительных межатомных расстояниях потенциальная энергия условно принимается равной нулю, так как при большом общем объеме, в котором находятся атомы, они не взаимодействуют. По мере сближения атомов потенциальная энергия уменьшается. Поскольку межатомным расстоянием в твердых телах соответствуют минимальные энергии, твердые тела существуют и при отсутствии внешних сжимающих сил. При некотором критическом расстоянии г0 потенциальная энергия достигает своего минимума Wumb а затем при
|
Рис. 2.18. Изменение сил (а) и энергии (б) в зависимости от расстояния между взаимодействующими частицами |
|
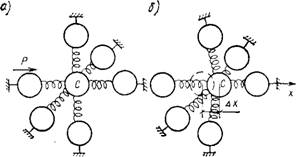
Рис. 2.19. Схема колебаний атома С А— в положении равновесия; б — при смещении вдоль оси х |
ГСГ0 она быстро возрастает, и это обусловливается тем, что плотность твердого тела является конечной величиной.
С физической точки зрения наибольший интерес представляет участок кривой вблизи точки минимума, где атомы не испытывают действия какой-либо результирующей силы, возникающей при взаимодействии атома с ближайшими соседями. В этой связи, следуя положениям работы [121], рассмотрим модель, состоящую из группы атомов твердого тела, жестко закрепленных на своих местах, и предположим, что центральный атом С Может под влиянием каких-либо сил перемещаться. Связь между атомом С и остальными изобразим в виде упругих пружин (рис. 2.19).
В первом приближении принимается, что длина пружин вдоль осей Z и у не изменяется (линейно-плоская модель). Предположим также, что под действием силы Р центральный атом С переместился относительно своих соседей в направлении х на расстояние Дл; (рис. 2.19, б). В этом случае между атомами возникают неуравновешенные силы, которые вызовут в пружинах деформации растяжения и сжатия в направлении х. Кривая на рис. 2.18,6 собственно и выражает характер изменения энергии атома с изменением расстояния между ним и соседними атомами. Если же изменяется расстояние только по отношению к одному атому, то энергию Wa(X) необходимо разделить на число ближайших соседей 5. Тогда энергия Д W^ связанная с изменением координаты атома С от Хо до х, т. е. на величину перемещения Дх, выразится уравнением
AWa = (2/5) [Wa СX - А*) + WА (*Ь + Д*) - 2VА (*о)]. (2.47)
Первый член этого уравнения характеризует энергию центрального атома с правым соседом, а второй — с левым. Коэффициент 2 введен потому, что перемещение атома С относительно его соседа вызывает равные изменения энергии у смещенного и неподвижного атомов.
Если функцию Wa(X) с минимумом в точке г0 разложить в ряд Тейлора, то общее изменение энергии атома С и его соседей при малых смещениях будет равно
A W = (2/S)(d2WJdx*)Xo( Ах)2 = а (Д*)« (2.48)
Где
А = WS)(d*WJdx*)Xo, (2.49)
Согласно закону изменения потенциальной энергии (2.48), центральный атом можно рассматривать как простой гармонический осциллятор, а это значит, что все атомы под действием силы Р совершают гармонические колебания (вибрируют) относительно своих равно
весных положений. Следовательно, сила Р, действующай на каждый атом, является функцией его смещения, т. е.
Р = — д (№0)/(дх) = — а (А*). (2.50)
Дифференциальное уравнение, описывающее движение атома массой та, имеет вид
Решение этого уравнения известно: Дл: = Ал Cos
К K/т» T.
В связи с этим угловая частота равна
Со = Vk/Ma, (2.53)
А частота колебаний атома (или эйштейновская частота)
|
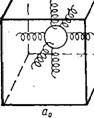
Рис. 2.20. Элементарный куб вокруг атома |
Будет выражаться зависимостью
(2.54)
Величину K обычно принимают за коэффициент пропорциональности между восстанавливающей силой и смещением, однако такая интерпретация не вполне физически обоснована.
|
(2.51) |
|
(2.52) Колебаний атома |
Допустим, что к элементарному кубу с ребром ао, внутри которого атом удерживается в некотором равновесном положении упругими связями (рис. 2.20), применим закон Гука. Если теперь к элементарному кубу приложить растягивающую силу Рр, тогда в направлении ее действия ребро куба удлинится на Аа0. В таком случае имеем
|
(2.55) |
|
Р/«о» |
Е = ка0/а9 = Рр1а{
Или
|
(2.56) |
|
(2.57) |
Да0 Е = Рр! а0.
Коль скоро упругая деформация материала определяется равнозначными деформациями межатомных связей, учитывая (2.54), можем написать
K — АА0 Е,
Отсюда следует, что K не безразмерный коэффициент, а сила, приходящаяся на единицу длины ребра элементарного куба. Другими словами, K можно расценивать и как восстанавливающую силу, приходящуюся на единицу длины межатомных связей при упругом деформировании материала.
Приведенная модель позволяет рассмотреть ряд процессов, происходящих в реальных твердых телах и структурированных системах, если соответствующим образом учесть, что соседние атомы в них также перемещаются. При анализе всех возможных движений атомов и атомных комплексов установлено [121], что частоты собственных колебаний их могут изменяться от 3-Ю12 Гц вплоть до низкочастотных (звуковых) колебаний. Каждое отдельное механическое колебание называется фоно- ном и смещение любого атома в кристалле или более крупных частиц в реальных твердых телах определяется суммированием всех фононов, каждый из которых характеризуется амплитудой и частотой колебаний.
Учитывая изложенное, модель цементного геля можно представить в виде системы из множества материальных точек rriu т2,..., mn, соединенных одна с другой упругими силами — пружинами ku k2,...,kn+. Для упрощения такую сложную систему удобно рассматривать как совокупность связанных между собой колебательных систем, каждая из которых обладает одной степенью свободы. В этом случае, определив свойства отдельных составляющих сложной системы, не трудно представить себе механическое поведение всей системы в целом [8, 27, 129, 151].
При разделении сложной связанной системы на части поступают следующим образом: закрепляют все точки системы, кроме первой, получают первую систему с одной степенью свободы; затем, закрепив все точки, кроме второй, получают вторую систему с одной степенью свободы и т. д. Перебрав аналогичным образом все точки сложной системы, будем иметь s — систем, для каждой из которых характерна одна степень свободы. Такие системы называются парциальными (например,
Допустим, что две массы — гп и т2 и пружины Ku Fa, их связывающие, одинаковы (рис. 2.21,а). Закрепим массу пг2 и отклоним массу т в направлении, перпендикулярном к пружинам (рис. 2.21,6), тогда эта
|
|
|
|
|
Рис. 2.21. Колебания связных (парциальных) систем |
Масса будет совершать гармонические колебания, если пренебречь затуханием. Собственная частота полученной таким образом парциальной системы — первая парциальная частота определится величиной массы т и упругостью пружин K и K2. Далее, если закрепить массу т И отклонить массу т2 (рис. 2.21, в), то она будет совершать такие же колебания с той же частотой, образуя вторую парциальную систему. Если освободить обе массы гп и т2, тогда образуются две парциальные системы со связанными частотами колебаний. В этом случае движение каждой из масс изменяет напряжение пружины kz, и сила действия ее на одну из масс определится положением другой массы.
Для возбуждения собственных колебаний в системе (рис. 2.21, а) обеим массам—Гп и т2 надо сообщить начальные отклонения. Допустим, что массы' получили равные по величине отклонения и в одну сторону (рис. 2.21, г), тогда пружина K2 не сообщит ускорения обеим массам, и они будут испытывать действие лишь одинаково растянутых пружин K и Массы гп и т2 будут совершать колебания в той же фазе с одинаковой частотой, которая меньше, чем парциальные частоты обеих систем, так как в рассмотренном случае восстанавливающая сила меньше по величине, чем у каждой из парциальных систем.
При одинаковых начальных отклонениях в разные стороны (рис. 2.21,(3) каждая масса окажется под действием не только одинаково растянутых пружин k и но и пружины K2. В связи с этим в каждый момент времени отклонения масс будут равны по величине и противоположны по знаку; они окажутся в состоянии гармонических колебаний с одинаковой частотой, однако противоположных по фазе, поэтому частота колебаний превзойдет общую парциальную частоту обеих связанных систем.
При соответствующем выборе начальных отклонений можно привести обе массы в состояние гармонических колебаний с одной из двух различных частот. Одна из них будет лежать выше общей парциальной частоты связанных систем, а другая — ниже. Эти частоты именуются нормальными, или частотами связи, а гармонические колебания, соответствующие им, называются нормальными колебаниями. В общем случае при произвольных начальных условиях в каждой из связанных систем могут возникнуть единовременно оба нормальных гармонических колебания с различными частотами.
При сложении двух разночастотных гармонических колебаний с одинаковыми амплитудами возникают биения; амплитуда колеблющейся массы, периодически изменяющаяся от максимума до нуля, будет постоянно уменьшаться, пока эта масса не остановится. В этот момент в колебательное состояние с возрастающей амплитудой придет вторая масса, находившаяся ранее в покое, и под ее действием вновь начнут постепенно нарастать амплитуды колебаний первой массы, в процессе которых станет затухать амплитуда колебаний второй массы. Такая картина возбуждения одного из нормальных колебаний или обоих нормальных колебаний одновременно может повторяться при явлениях биения многократно. В рассмотренных случаях энергия от одной колебательной массы «перекачивается» к другой через упругую связь (пружину). Действуя через нее, первая масса раскачивает вторую и, хотя амплитуда колебаний первой массы и убывает, она все время опережает вторую массу, продолжая ее раскачивать даже тогда, когда амплитуда второй становится больше, чем первой. Раскачивание может прекратиться после остановки первой массы, однако в этот момент вся энергия перейдет ко второй массе и она начнет раскачивать первую массу; энергия снова возвращается к первой массе, и этот процесс будет повторяться в указанной последовательности.
Частота биений и скорость флуктуации энергии зависят от разности частот нормальных колебаний и чем она больше, тем больше частота биений и быстрее «перека- ^йЁаетсй» Эйергйя. 6 этой связй проаналйзируем Поведение модели (рис. 2.21, а) при изменении упругости пружины постепенно ее растягивая, не нарушая равновесия обеих масс —mi и т2. Если сильно растянуть пружину K2 (сделав ее очень мягкой), расстояние между массами Rri и т2 значительно увеличится и при их отклонениях напряжение в пружине K2 будет изменяться малоощутимо, т. е. влияние последней окажется все менее заметным и связь между системами будет все более ослабевать. Поскольку различие в нормальных частотах и их отличие от общей парциальной частоты связанных систем обусловлены в том или ином случае напряжением (упругостью) пружины k2y то чем меньше ее влияние, тем меньше будет указанное различие в частотах и ближе к парциальной частоте обеих систем окажутся обе нормальные частоты. Следовательно, с ослаблением связи между двумя системами биения, возникающие в связанных системах, будут проявляться медленнее.
Даже при отсутствии сил трения и очень слабой свя - &и нормальные колебания имеют различные частоты, поэтому явления биения в связанных системах происходят весьма медленно. Поскольку же вследствие наличия трения (сопротивлений) колебания в связанных системах постепенно затухают, то при очень слабой связи они успевают затухнуть раньше, чем ощутимая доля энергии успеет перейти от одной системы к другой, т. е. тогда биения не будут вовсе наблюдаться.
В общем случае каждой парциальной системе присущи две нормальные частоты, несовпадающие с парциальными частотами двух связанных систем. Одна из нормальных частот лежит ниже меньшей из парциальных частот, а другая — выше большей из парциальных частот. Чем слабее связи между системами, тем ближе находятся нормальные частоты к обеим парциальным частотам.
Под влиянием внешних динамических импульсов (например, вибрации) в связанных системах возникает явление резонанса, проявляющееся всякий раз, когда частота гармонической внешней силы совпадает с одной из двух нормальных частот ©i и ю2 системы. Это явление можно квалифицировать как случай, когда под действием внешней гармонической силы система совершает «почти собственные» колебания. При этом роль внешней силы сводится главным образом к преодолению прочно
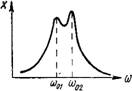
сти связей и сил трения (вязкости) системы. Поскольку каждая связанная система может совершать колебания с нормальной частотой, ей присущей, то при определенных частотах внешнего механического воздействия резонанс будет проявляться только в отдельных системах, т. е. локально. При медленном изменении частоты возбудителя колебаний резонанс наступает дважды при совпадении с каждой из частот связанной системы; в этом случае резонансная кривая будет иметь двугорбый вид (рис. 2.22).
Если связать два одинаковых резонатора, то они будут реагировать не на каждую порознь взятую парциальную частоту системы, а на две одинаковые частоты, из которых одна находится выше, а другая ниже собственной частоты резонатора. Такой характер совпадения (расщепления) частот проявляется тем выразительнее, чем сильнее связи между резонаторами. Для того чтобы система вошла в резонанс, необходимо определенное время и тем большее, чем быстрее завершается процесс затухания колебаний.
При огромном количестве взаимосвязанных парциальных систем, составляющих цементный гель с различными по степени упругости связями, колебательные явления протекают гораздо сложнее. Однако, несмотря на это, основные положения, приведенные выше, сохраняются в силе.
|
Рис. 2.22. Двухгорбая реЗонансная кривая |
Из приведенного можно заключить, что под влиянием механического (вибрационного) воздействия цементный гель колеблется не как одно целое, сплошное тело. В зависимости от распределения масс цементных частиц резонансные явления, способствующие псевдоразжижению цементного геля, должны происходить вначале в микрообъемах цементного геля; затем в колебательный процесс постепенно (как бы по цепной реакции) вовлекаются остальные «парциальные системы», и по мере «перекачки» колебательной энергии возникают резонансные явления при совпадении частот вынужденных колебаний с одной из двух нормальных частот каждой «парциальной системы». В этом случае резонансные кривые обра
зуют многогорбую рельефную поверхность, а сам процесс разжижения цементного геля будет уподобляться процессу, происходящему в так называемом кипящем слое.
В зависимости от водосодержания тиксотропное разжижение цементного геля, происходящее вследствие вовлечения всего его объема в состояние резонанса, может происходить, как это уже было отмечено, при различных частотах вынужденных колебаний. Это очевидно, так как с увеличением количества воды ослабляются внутренние связи между отдельными парциальными системами цементного геля, снижается уровень частотного спектра собственных колебаний масс цементных частиц, медленнее перекачивается энергия, слабее сказывается влияние явлений биения, поэтому такая система меньше реагирует на резонансную частоту вынужденных колебаний.
Например, при X, близком к 1,65, частота возбудителя колебаний может совпадать с парциальной частотой одной из связанных систем, а не с одной из нормальных частот. Вследствие значительной неоднородности цементного геля с групповой разобщенной структурой две какие-либо связанные системы всегда будут отличаться парциальными частотами. Частота вынужденных колебаний может действовать только на одну из систем, имеющую созвучную с импульсной силой парциальную частоту, и она придет в очень слабое колебательное состояние. Здесь не исключена возможность, что во второй системе (находящейся вне поля непосредственного влияния возбудителя) парциальная частота будет совпадать с частотой внешней силы и это может спровоцировать очень сильное колебание. Однако маловероятно, чтобы при этом возникли резонансные явления, так как первая система со слабыми колебаниями будет играть роль «ускорителя» колебаний по отношению к сильно возбужденной второй парциальной системе. Отсюда можно придти к выводу, что явление резонанса, обусловленное совпадением частот собственных колебаний с частотами вынужденных колебаний, связано с возникновением благоприятных условий для поступления в систему определенного количества энергии от источника внешней силы. Такая энергетическая ситуация наступает в основном в связанных однородноплотных парциальных системах при близком совпадении частот вынужденных колебаний с одной из нормальных частот возбуждаемой системы.
Собственное колебание какой-либо материальной частицы связанной системы, возникает в том случае, когда при быстро изменяющейся силе за период колебаний частице сообщается толчок и она приходит в колебательное движение. Частота собственных колебаний соо определяется свойствами самой системы и для рассмотренных осциллирующих систем может быть вычислена по формуле (2.54), т. е.
Со — (2.58)
2тс
Восстанавливающую силу ky приходящуюся на единицу длины связи у между цементными частицами при ее «упругом» деформировании под влиянием вибрационных колебаний (в случае обратимой тиксотропии цементного геля), можно определить в соответствии с формулой (2.57) зависимостью
K = Yxy. (2.59)
Величина хуу характеризующая предел упругости цементного геля при сдвиге, может быть принята по соотношению Ту^0,5то - Следовательно:
K = 0,5//т0. (2.60)
Если выразить массу частиц m через условный диаметр d, тогда при известной частоте вынужденных колебаний сов, соответствующей тиксотропному превращению цементного геля при данной его консистенции, по формуле для соо можно вычислить значения K:
K = 0,063(Dg D3. (2.61)
Затем, зная K и ту> нетрудно определить у из соотношения (2.61), т. е.
У = к! ту.
Наиболее достоверные результаты вычислений могут быть получены при значениях Х=0,876 и 1, поскольку в этих случаях с большей точностью удается экспериментально замерить частоты вынужденных колебаний (вибрации) сов.
Ранее было показано [4], что мельчайшие фракции, до 80% которых содержится в современных цементах, не способны существовать разрозненно в силу поверхностно-активных явлений и объединяются в агрегаты (фло - кулы) крупностью примерно 25 мкм и более. Агрегаты порядка 25 мкм обладают большими резонансными свойствами, чем более крупные, так как нормальные частоты первых находятся выше последних. Можно принять, что с учетом сольватного слоя воды диаметр таких агрегатов достигает 30 мкм, а масса их т=0,435-10~10 гХ Хс2/см. Поскольку при Х=0,876 т0=1040 Па, будем иметь Ту =£30 Па; £=6,8-10~5 и у= 1,27• 10~6 см. Аналогично получим при Х= и то—134 Па; & = 1,7-10~5 и У— 1,27-10—6 см (0,0127 мкм). Принимая у за величину постоянную, можно вычислить k, а по нему соо для всех значений X цементного геля (табл. 2.2).
|
ТАБЛИЦА 2.2. ЗАВИСИМОСТЬ МЕХАНИЧЕСКИХ ПАРАМЕТРОВ ОТ РАЗЛИЧНЫХ ЗНАЧЕНИЙ X
|
Полученные значения частот собственных колебаний соо следует рассматривать как максимальные для соответствующей консистенции цементного геля, и здесь уместно отметить, что величины сов вполне удовлетворительно согласуются с частотами вынужденных колебаний, при которых достигается разжижение цементного геля.
Если масса цементной частицы окажется выведенной из состояния покоя силой, величина которой изменяется по гармоническому закону, то установившееся (с постоянной амплитудой) колебательное движение будет в той или иной мере повторять характер движения внешней силы. В этом случае в области резонанса упругая связь помимо внешней силы сообщает массе частицы т необходимое ускорение, и роль возбудителя колебаний сводится только к преодолению силы вязкости (трения).
Как уже было отмечено, при возникновении внешней силы всегда возбуждаются собственные колебания, которые затем трансформируются в вынужденные, поэтому картину колебательного процесса можно рассматривать как наложение двух явлений: собственных колебаний, вызванных включением внешней силы, и вынужденных колебаний, создаваемых постоянно действующей в течение определенного времени гармонической внешней силой. При резонансе частоты этих двух колебаний совпадают, и, следовательно, смещение (деформацию связей) колеблющейся системы можно [95, 125] выразить следующим образом:
Г = A0e~^at sin (со0 T + I|?c) + Ав Sin (сов T + ф), (2.62)
Где ао — начальная амплитуда собственных колебаний; ав — амплитуда вынужденных (установившихся) колебаний; и ср — их фазы.
При подключении внешней силы 2=0 и v = dz/di = 0. Тогда, подставляя в соотношение (2.62) /=0, получим
А0 Sin I|?G + ав Sin Ф = 0. (2.63)
С другой стороны, если показатель затухания собственных колебаний а^соо, то дифференцируя выражение (2.62) и пренебрегая величиной аао по сравнению с аоо>о, приближенное значение скорости колеблющейся системы можно выразить уравнением:
V « со0 a0e~at Cos (со0£ + I|?C) + <ов ав Cos (сов t + ф) • (2.64) Принимая в (2.64) /=0 и и = 0, получим
А0 Costc + ^в Cos(P = 0. (2.65) Из соотношений (2.63) и (2.65) следует, что
Со = «в; <Фс = Ф + я.
Таким образом, при противоположно направляемых фазах амплитуда собственных колебаний равна амплитуде вынужденных колебаний, в связи с чем результирующее смещение, определяемое выражением (2.62), будет иметь вид:
Z = ав (1 — E-at) sin (сов / + ф). (2.66)
Результат сложения обоих колебаний выражает собой такое колебательное движение, когда амплитуда его нарастает до значения ав по закону 1—E~at.
Из выражения (2.62) можно заключить, что вследствие затухания собственных колебаний в системе останутся одни вынужденные колебания; чем меньше затухание системы, тем больше времени потребуется пока затухнут собственные колебания и будет дальше длиться процесс установления равновесия. Это означает, что чем резче выражены резонансные свойства, тем продолжительнее процесс, при котором возникает резонанс.
Явление резонанса и вместе с этим разжижение цементного геля наблюдается только в том случае, когда за время установления вынужденных колебаний резонаторов внешнее гармоническое воздействие не прекращается и его динамические параметры не изменяются.
Характер нарушения связей между частицами при проявлении тиксотропии цементного геля может быть в какой-то мере уподоблен механизму упруговосстанавли - вающейся деформации. В самом деле, в условиях установившихся резонансных колебаний частицы твердой фазы колеблются в режиме внешней гармонической силы, а поэтому процесс разрушения связей должен чередоваться с периодическим их восстановлением в моменты, когда амплитуда колебаний приближается по величине к нулевому значению. Эти промежутки времени численно равны периоду колебаний, т. е.
Т = 2nVmTk. (2.67)
Учитывая, что со0=2 я V m/k> можно написать
Г = 1 /со0. (2.68)
Подставляя в (2.68) значения о)о, соответствующие структурной прочности цементного геля при различных X (табл. 2.2), получим: при о)0 = 200 Гц—Т=0,005 с; при о)о= 100 Гц — Т=0,01 с; при со0=50 Гц —Т=0,02 с и при о)о= Ю Гц — Т=0,1 с.
Из этих данных следует, что с увеличением структурной прочности цементного геля промежутки времени, в течение которых в области резонансных колебаний восстанавливаются разрушенные внутренние связи между частицами, значительно сокращаются, поэтому для поддержания разжиженного состояния частота колебаний внешней силы должна быть тем выше, чем меньше воды в цементном геле и прочнее в ней структурные связи. Эта особенность структурных связей периодически восстанавливаться при резонансных колебаниях частиц твердой фазы под влиянием внешних гармонических воздействий и определяет обратимый характер тиксотропии структурированных гелей, т. е. обратимый переход из состояния геля в золь и, наоборот, из золя в гель (гель^золь).
Таким образом, из всего рассмотренного можно сделать вывод, что в общем случае нельзя отождествлять тиксотропное состояние цементного геля и подобных ему структурированных систем с проявлением броуновского
(неупорядоченного теплового) движения, для которого требуется достаточное количество жидкой фазы. Резонансный характер псевдоразжижения свидетельствует о том, что это явление может наблюдаться и при отсутствии в системе свободной жидкости.
При разжижении возникают условия для активизации сил, способствующих уплотнению цементного геля. В процессе разрушения структурных связей между частицами некоторый объем жидкости диффузного слоя переводится кратковременно в состояние обычной вязкой жидкости и освобождается часть поверхностной энергии. Вместе с этим вследствие дезагрегации флокул возрастает число частиц цемента, вокруг которых ориентируются молекулы воды, образующие адсорбционный и первые слои диффузной оболочки. Происходящее перераспределение воды создает благоприятные условия для более близкого порядка во взаиморасположении цементных частиц в момент прекращения внешнего механического воздействия на цементный гель. В результате происходит дополнительное стяжение (конструкция) объема цементного геля (по сравнению с первоначальным объемом), способствующее его уплотнению.

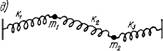
 Опубликовано в
Опубликовано в