Для того чтобы правильно организовать вращение ножки дуги пе­ременного тока переменным магнитным полем, необходимо иметь рас­четные формулы для определения напряженности магнитного поля внутри электрода и фазового сдвига.

Рассмотрим соответствующую задачу в следующей постановке. Имеется бесконечный соленоид с числом витков на единицу длины, равным wt по которому протекает переменный ток /. Эффективное значение напряженности магнитного поля, создаваемого этим соле­ноидом, по определению равно = Iw. Внутрь соленоида помещен

полый немагнитный проводящий цилиндр (рис. 6.5). Требуется найти напряженность магнитного поля в полости внутри цилиндра и сдвиг фазы этого поля относительно поля на внешней поверхности цилиндра (совпадающего по фазе с током в соленоиде). Точное решение этой задачи может быть получено из уравнений Максвелла. Пренебрегая токами смещения, запишем эти уравнения в безразмерной форме от­дельно для стенки цилиндра и для его внутренней полости:

а) в металле

->

* * 3 н

rot Н = £ ; rot Ґ = - у -т-г - :

ММ М 0 1

б) в полости

->

♦ ЪН

rot Н = 0; rot Т = - у - гг-

п not

где Н = Н/Н: Е = о г Шл т — со/;

0 ср 0

г - г/г = 2r/d; у = а цла> г ;

ср 0 ср

HQ - напряженность магнитного поля на внешней поверхности цилинд­ра; £ - напряженность электрического поля; а - удельная электро­проводность металла; г и d - средний радиус и диаметр цилиндра;

ср

черточками обозначены размерные величины; м, п - индексы металла и полости.

Предполагается, что все переменные во времени величины изме­няются по синусоидальному закону, поэтому далее всюду пользуемся символическим методом, т. е. эти величины записываются в виде

А = А ЛЕ -|i = j 'A

т дт '

Ц = ГГ). Тогда уравнения принимают следующий вид:

а) в металле

rot Н = £ ; rot £ = -}уН ; (6.4)

ММ мм

б) В ПОЛОСТИ

rot Н = 0; rot Е = - jyH. (6.5)

п п п

Для нахождения Н необходимо решить системы (6.4) и (6.5) и сты - п

ковать полученные решения на границе, т. е. при г = г(. Граничное условие для системы (6.4) следующее:

Н = 1 при г =г^.

Условия стыковки на границе:

при г = г, Н = Н, £ = £ .

I м п м п

Из системы уравнений после исключения Е получаем дифференциальное

М

уравнение Бесселя

Ъ2Н /Ы2 * 1/гЪН /Ьг - jyH = О,

м мм

решение которого имеет вид

Нм = AIQ(r Щ ♦ ВК0(г Гр}),

где /q и Kq - модифицированные функции Бесселя первого и второго порядка; А и В - постоянные интегрирования. Далее находим £М = - f/7 [аі{(г Щ - ВК,(Г щ].

где и К - те же функции, но первого порядка. Решение для получаем непосредственно: = const, а для Е^ имеем уравнение

ЪЕ /Ъг + Е /г = - jyH,

п п п

откуда с учетом условия ограниченности Е^ на оси находим

1угНп.

Таким образом, с учетом условий стыковки решений на границе "ме­талл - полость" получаем следующую систему уравнений для опреде­ления Н : п

W+ BW= 1:

АІЛх ) * ВКЛх ) = Н ; (6.6)

0 1 0 1 п

где ж = г fjy. Выражение для х можно преобразовать следующим об­разом:

г 4?

— ; х = г 457л.

_____ — 1/2

где £ = (2/oji^cj) - глубина проникновения плоской электромаг­нитной волны в полуограниченное тело, которая определяется как расстояние от поверхности, на котором напряженность поля умень­шается в е раз. Для плоской электромагнитной волны £ зависит только от свойств металла о ид (для ферро - и диамагнетиков) и частоты со, тогда как для цилиндрических электромагнитных волн £ зависит также и от радиуса цилиндра.

Модуль и фаза комплексного числа дают соответственно уменьшение

напряженности магнитного поля в полости и фазовый сдвиг по отно­шению к току в соленоиде.

Формула (6.7), хотя и представляет собой точное решение по­ставленной задачи, неудобна для практических расчетов. Поэтому изложим упрощенный метод расчета, который назовем "методом транс­форматора”. Он заключается в том, что соленоид рассматривается как первичная обмотка трансформатора, а металлический полый цилиндр - как вторичная короткозамкнутая обмотка (один виток). При этом дифференциальные уравнения Максвелла заменяются соответствующими интегральными уравнениями. При расчете делается предположение о том, что внутри полости цилиндра напряженность поля однородна по радиусу и длине, т. е. отношение длины цилиндра к его диаметру достаточно велико и краевые эффекты можно не учитывать. В этом случае полем вне соленоида можно пренебречь. Тогда на основании закона полного тока

m dT = Z/ю

можно записать (в размерном виде)

HI = /о»; HI =11 * lw, (6.8)

где /( - сила тока в цилиндре. Далее задача заключается в на­хождении / .

ЭДС, наводимая во вторичном витке, е = - ЭФ/Эг, или £^ = - /<оФ,

где Ф = а/Ф - потокосцепление, а Ф = SpdidS - магнитный поток. Тогда

Ф = nd^nQH; Ф = Ф(так как = 1); £( = - jcjnr^n^H.

Пусть активное сопротивление' вторичного витка равно Я.

Тогда

*1 2 '

/, = - j - = - ivnrnQH/Rx. (6.9)

Необходимо отметить, что в этой формуле отсутствует индуктивность вторичного витка L. Это объясняется тем, что введением в рас­сматриваемую формулу Н вместо Hq мы уже учитываем размагничивающее

действие вторичного витка, определяемое его индуктивностью.

Очевидно, что при принятых предположениях индуктивность катушки

f У 2 2,-1

L = -у - = ц^ттг w I ; соответствующее индуктивное сопротивление

2 2—1

X£ = CjL, ИЛИ X£ = Д^СаЛГГ W I. (6.10)

При вычислении индуктивного сопротивления по этой формуле допус­кается ошибка в сторону увеличения по сравнению с истинным зна­чением. Величина этой ошибки зависит от отношения Hr и равна

ср

приблизительно 30 % при Hr = 2 и 10 % при Hr = 6.

ср ср

Подставляя (6.9) в (6.8) с учетом (6.10), получим

«Ч = *,«, * і’ґ-

откуда, обозначив а( = x^/R^, имеем Н/Н0 = (1 ♦ /а,)'1;

H/HQ = Н/Н0 = (1 + afU (6.11)

tg * = - а,- (6.12)

Активное сопротивление вторичного витка

/?j = itd/olS,

откуда

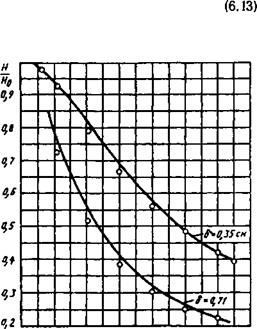о, = 0.25м0<о»&г.

Для меди при f = 50 Гц

aI = 0,55dS[cM2].

Таким образом, по форму­лам (6.11...6.13) можно рассчитать ослабление поля и фазовый сдвиг.

Рнс. 6.6. Уменьшение на­пряженности магнитного

поля. при прохождении электромагнитной волны

через стенку цилиндра:

---------- точный расчет;

О — приближенный расчет

Рис. 6.7. Зависимость
фазового сдвига от ра-
диуса цилиндра:

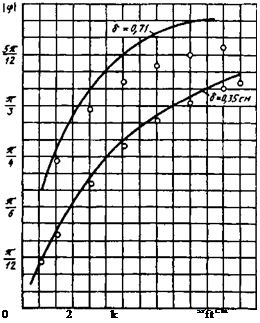--------- точный расчет:

О — приближенный расчет

Сравним результаты, полученные по точной теории и по методу трансформатора. На рис. б. б приведены соответствующие зависи­мости ослабления поля в полости цилиндра для двух толщин сте­нок, а на рис. 6.7 - аналогичные зависимости для фазового сдви­га. Приведенные кривые показывают, что расчет по методу транс­форматора дает высокую точность при относительно малой толщине стенки. С увеличением толщины стенки точность ухудшается, однако для применяемых на практике электродов является вполне удов­летворительной. Максимальная ошибка при определении Н/Н^ со­ставляет приблизительно 2 % при толщине стенки 8 = 0,35 см и 5 % - при 8 = 0,71 см, при определении ф - соответственно 4 и 10 %. Уменьшение точности с увеличением толщины стенки связано с воз­никающей в этом случае неравномерностью распределения тока в стенке цилиндра из-за поверхностного эффекта, что не учитывается в методе трансформатора.