Природа диэлектрических потерь
 19 декабря, 2013
19 декабря, 2013  admin
admin У неполярных полимеров дипольные потери в области Т—Т2 (рис. 7.3, а) отсутствуют и проявляются только потери проводимости, вызывающие рост tg б при Т>Т2.
Любой диэлектрик можно представить в виде параллельно или последовательно соединенных емкости С и активного сопротивления1R. В первом случае tg 6= 1/(сoCR), а во втором tg б = соС/?.
Другой тип энергетических потерь в диэлектриках связан с электронной РЭл и атомной Рат поляризациями, обусловленными смещениями (ток смещения) под действием электрического поля электронов, ядер, ионов или атомных групп (резонансное поглощение). Для практического применения диэлектриков представляет интерес рассмотрение деталей перехода от установившейся полной поляризации при низких частотах к поляризации при оптических частотах, так как они непосредственно связаны с разделением поляризации при низких частотах на ее составляющие: ориентационную и деформационную (атомную и электронную). Резонансные потери проявляются при частотах 1010—1013 Гц (миллиметровая и инфракрасная области длин волн). Существование их у полимеров обусловлено наличием собственных колебаний атомных групп. Некоторые полосы поглощения в инфракрасной области связаны с трансляционными движениями диполей. Характер изменения потерь энергии при этом имеет сходство с соответствующими зависимостями при дипольной релаксации. Мнимая составляющая г" обобщенной диэлектрической проницаемости 8* изменяется в окрестности резонансной частоты примерно так же, как и при дипольной релаксации (проходит область максимума), хотя потери энергии в этом случае имеют другую природу и требуют иного аналитического описания. В то же время диэлектрическая проницаемость 8 при дипольной релаксации и резонансном поглощении изменяется по-разному.
Процесс, приводящий к резонансному поглощению энергии, можно^ описать следующим образом. Если электронное облако смещается от своего нормального положения относительно ядра, то возникает сила, стремящаяся вернуть его в исходное положение. Эта сила является сложной функцией смещения, но можно предположить, что при смещениях, характерных для электронной и атомной поляризаций, она является линейной. Дифференциальное уравнение для смещения г имеет вид
|
(7.7) |
d2r. 2
т —+mco0r=^E*.
|
(7.8) |
Здесь Е* — напряженность локального поля; ю0 — характеристическая частота, связанная с силовой постоянной k и массой осциллятора т соотношением coo2 = k/m. В простейшем случае при г = х получим
Е*=Е=Е0 ехр (— Ш).
Движущиеся с переменной скоростью заряды излучают электромагнитную энергию. В описанном выше простом гармоническом осцилляторе заряды постоянно ускоряются или замедляются. Следовательно, они излучают энергию, являющуюся частью энергии колебаний, которые со временем затухают. Кроме того, атомы и ионы исследуемого вещества постоянно испытывают соударения (они происходят хаотически в течение периода колебаний и носят неупругий характер) с другими атомами и ионами.- Следовательно, энергия диэлектрических колебаний может превращаться в результате столкновений в теплоту. Оба типа потерь могут быть приближенно описаны диссипативным членом, пропорциональным dr/dt. При этом уравнение (7.7) с учетом условия (7.8) для выбранного направления х запишется в виде
|
(7.9) |
т ~йП +т* ~£+kx=qE'fi-h‘t,
где f — характерное для данного вещества значение диссипации. Решение уравнения (7.9) дает временную зависимость поляризации каждого отдельного атома, что позволяет вычислить его поля - ризованность. Используя последнюю, можно рассчитать и диэлектрическую проницаемость.
Решение уравнения (7.9) можно найти путем подстановки в него выражения с неопределенным коэффициентом:
|
(7. Ю} |
х=аегш.
Оно удовлетворяет заданному дифференциальному уравнению при условии, что
|
Дипольный момент каждого атома может быть представлен как сумма двух компонентов: синфазного и смещенного по фазе. Ди- |
польный момент каждого единичного диполя P = qx, а поляризо - ванность среды, содержащей N диполей в единичном объеме,
P=Nqx. (7.12)
С учетом соотношений (7.10) — (7.12) для обобщенной диэлектрической проницаемости получаем
-*=11 4дДГ#2 /• сор —__________________________ г/CD
/И ( U)q — 0)2)2 + /2Ш2 ( со2_ W2)2 д./2^2 Г
|
|
|
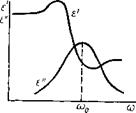
Рис. 7.4. Частотная зависимость действительной и мнимой составляющих комплексной диэлектрической проницаемости для резонансного механизма поглощения |
Действительная е и мнимая е" части комплексной диэлектрической проницаемости при этом равны:
1 ( ЫЫд2 (coq — ш2)
£— ‘ т [(а)2-ш2)2+ /2Ш2] ’
4nNq2 ______ /ш____
TTL (o)q — (i)2)^ - j - у2ц)2
Для статического случая, когда ю = 0, е = 1 +4лЛ^2/т, а при о—>-оо е=1. Значение как при со->0, так и при со—^оо (рис.
7.4), а при со = озо оно проходит через максимум: 8шах =
= 4TiNq2/(mf($o). Сдвинутый по фазе компонент е" так же характеризует энергетические потери, как и в случае релаксации дипольной поляризации. Резонансное поглощение для полимеров менее существенно, чем дипольные релаксационные потери. В случае резонансного поглощения области максимума г" и изменения s существенно уже, чем при релаксационных процессах.

 Опубликовано в
Опубликовано в