Современная физика не оперирует абсолютными скоростями в абсолютном пространстве-времени, а все измерения производится только как относительные измерения. По этой причине в научной литературе отсутствуют сведения об исследования движения частицы (тела) в абсолютном пространстве с учетом абсолютной скорости, хотя такие исследования сами по себе заслуживают внимания, поскольку позволяют получить уникальные результаты. Учитывая реалии абсолютного квантованного пространства - времени как специфической упругой квантованной среды, исследования абсолютного движения позволили записать баланс энергии (75) частицы (тела) во всем диапазоне скоростей v от 0 до С0

W = wmax - Ws = Ynmoc2 (98)

В области нерелятивистских скоростей v<<^ формула (98) переходит в (76)

В (99) входит энергия покоя Wo (56) и кинетическая энергия Wk частицы (тела) в области нерелятивистских скоростей

Wk=2m оv2

На самом деле, как было уже показано, энергия частицы (тела) в общем случае едина и определяется энергией (98) сферической деформацией квантованного пространства - времени, которая в свою очередь через нормализованный релятивистский фактор yn (70) связана со скоростью движения v. Сама частица (тело) не в состоянии измерить свою энергию или скорость, но в состоянии изменять концентрацию р2 и pi (77) квантонов внутри гравитационной границы и снаружи, обеспечивая скачек Др1 и Др2 квантовой плотности среды (рис. 11). Любой из параметров среды: p1, p2, Др1, Др2 определяет скорость v частицы (тела). Для удобства расчетов проследим изменение квантовой плотности среды р2 (77) внутри частицы (тела) в зависимости от скорости v

р 2 = р о

. Р о У

Функция (103) является неявной относительно изменения квантовой плотности Др2, но она позволяет точно определить абсолютную скорость v по величине приращения Др2 относительно ро. Это означает, что абсолютную скорость можно контролировать приборами,
если контролировать изменение квантовой плотности среды. Постулат Пуанкаре о том, что приборами невозможно это делать был рассчитан на уровень знаний в начале 20 века, когда понятия не имели о квантовой теории гравитации.

Анализ выражения (103) для значения абсолютной скорости v=0 и v=C0 дает четкие соотношения для параметров частицы (тела):

1.	при v > 0,	AP2 ^РoRg RS	(104)
2.	при v < Co,	о О. VI <N о. <	(105)

Во всем диапазоне скоростей от 0 до С0 изменение квантовой плотности среды будет увеличиваться от (104) до (105), увеличивая энергию сферической деформации квантованного пространства-времени в соответствии с (98). Но уже анализ кинетической энергии (100) частицы (тела) приводит к энергетическому парадоксу, природа которого связана со спецификой движения в квантованной среде.

Чтобы раскрыть причины энергетического парадокса, рассмотрим следующую задачу движения. Пушечное ядро массой m вылетело из ствола пушки и ударилось в крепостную стену с относительной скоростью Av, застряв в стене и частично ее разрушив. Необходимо найти абсолютную кинетическую энергию ядра в момент удара о стену, принимая абсолютную скорость пушки за v0, намного меньше скорости света Со и массу покоя ядра - m0. В первом приближении при решении решение задачи в области нерелятивистских скоростей можно пренебречь увеличением массы ядра от скорости, приняв m=m0, и компенсировав увеличение массы эквивалентным увеличением кинетической энергии.

В первом случае, посчитаем абсолютную кинетическую энергию Wk (100) ядра, подставив в (100) абсолютную скорость v=vo+Av

Wk1 = 2mv2 = 2m(v о + Av)2 = 2m(v 2 + Av2 + 2v о Av)

Во втором случае считаем, что к абсолютной кинетической энергии W^ ядра до выстрела из пушки, необходимо добавить кинетическую энергию AWk ядра, полученную в результате выстрела. Тогда абсолютная кинетическая энергия Wk2 ядра определиться определится суммой двух энергий:

Wk2=Wko+AWk=2mv2+2mAv2=2m(v 2+Av2) (107)

Находим разность AW энергий Wk1 (106) и Wk2 (107)

AW = W. J - W^ = mv0 Av (108)

Абсолютная кинетическая энергия Wk2 (107) ядра во втором случае соответствует эксперименту. Но и абсолютная кинетическая энергия Wk1 (106) также может соответствовать экспериментальным данным. Возникла парадоксальная ситуации, когда при достижение одной и той же абсолютной скорости v в квантованном пространстве-времени кинетическая энергия частицы может принимать два различных значения. Энергия Wk1 (106) завышена на величину mv0Av (108) по сравнению Wk2 (107). Сложившаяся ситуация известна в физике, но ее объяснение удалось получить только в теории УКС и ТЕЭП.

Причиной энергетического парадокса являются фазовые переходы в момент ускорения (торможения) частицы (тела), связанные с перераспределение квантовой плотности среды внутри оболочки элементарных частиц, входящих в состав вещества пушечного ядра (в том числе и атомных ядер). Это внутренняя специфика движения с ускорением, и если это движение с ускорением прерывается, то возникает указанный энергетический парадокс. Исследование фазовых переходов внутри оболочки элементарных частиц стало возможным благодаря достижениям квантовой механики открытых квантомеханических систем.

Чтобы понять причину энергетического парадокса вернемся к анализу сферической модель нуклона на рис. 11, которая включает внутреннюю и внешнюю области, разделенные гравитационной границей раздела с радиусом RS, роль которой играет знакопеременная оболочка нуклона. Внешняя область сферически деформированного квантованного пространства-времени определяет гравитационное поле нуклона, которое остается сферически инвариантным с увеличением абсолютной скорости частицы, вплоть до скорости света. В данном случае нас интересует внутренняя область частицы. Уже упоминалось, что с увеличением скорости v увеличивается квантовая плотность среды р2 (101) внутри оболочки нуклона за счет уменьшения квантовой плотности среды с внешней стороны. Теперь необходимо рассмотреть фазовые переходы квантовой плотности внутри оболочки частицы (тела) при ускорении (92).

Классическая физика рассматривает ускорение, как инерциальное свойство изолированной частицы (тела) в закрытой квантомеханической системе. Мерой инертности служит масса. Ни о какой внутренней связи частицы (тела) с квантованным пространством - временем, как открытой квантомеханической системе, в то время не могло идти и речи. Такая концепция ограничивала поле деятельности исследователя, не позволяя проникнуть во внутрь проблемы. Причины инерции связаны с фазовыми переходами квантовой плотности среды (93) внутри гравитационной границы частицы, когда градиентное перераспределение наблюдается в направлении действия ускоряющей силы только в момент ускорения, обусловленное переходным процессом изменения скорости движения (рис. 14).

Необходимо отметить, что процесс движения тела определяется всей совокупностью движения элементарных частиц в состав тела. Это процесс электромагнитный, учитывая электромагнитную структуру квантованного пространства-времени [1]. Оболочка нуклонов также состоит из электрических зарядов [14]. Электрон содержит центральный электрический заряд [10-17]. Квантованное пространство-время заполнено квантонами, которые включают два электрических и два магнитных монопольных заряда [1]. Сферическая деформация квантованного пространства времени, как процесс сжатия и растяжения квантонов, связан со смещением от равновесия электрических и магнитных зарядов внутри квантонов (1). Поэтому движение частицы (тела) - есть сложный динамический электромагнитный процесс. И как любой электромагнитный процесс он состоит из двух компонент: активной и реактивной составляющих. Активная компонента определяет наблюдаемые активные затраты или освобождение энергии. Реактивная компонента обеспечивает резонансный обмен электромагнитной энергией между частицей и квантованным пространством-временем.

Казалось бы, что движение по инерции не связано с энергетическим обменом, поскольку мы не наблюдаем внешнего воздействия сил на движущееся по инерции тело (частицу). Но это только внешняя сторона вопроса. Движение по инерции это, как уже отмечалось, есть волновой перенос сферической деформации квантованного пространства - времени, внешне наблюдаемый как перенос массы тела (частицы). Поэтому движение по инерции связано с обменными энергетическими процессами между движущимся телом (частицей) и квантованной средой, когда передний фронт тела (частицы) производит деформацию среды, затрачивая на это требуемую энергию, а задний фронт тела (частицы) сбрасывает деформацию среды, возвращая назад в среду, затраченную на деформацию энергию, обеспечивая соблюдение закона сохранения энергии. Это резонансный электромагнитный процесс обмена энергией при движении, обеспечивающий внутренний баланс реактивной энергии, внешне наблюдаемый, как свободное движение тела (частицы) по инерции.

Попытку определить сопротивление движения телу в вакууме предпринималась другими исследователями, в том числе И. Ярковским, который допускал, что вакуум оказывает сопротивление движению пропорционально кубу скорости [44]. Рассмотрим конкретные силы сопротивления движению нерелятивистской частицы в квантованной среде, ограничившись волновым переносом только массы покоя mo. Частицы при движении
описывает цилиндрическую трубку в пространстве, энергия деформации которой определяет энергию, затраченную на движение. Расчеты удобнее проводить для сплошной цилиндрической трубки в рамках гравитационной границы RS. Учитывая, что энергия деформации среды с внешней стороны, уравновешена энергией с внутренней стороны гравитационной границы, распределясь поровну, определим приведенную массу mv

2

цилиндрической трубки с плотностью вещества pm в удвоенном объеме V = П • R S •х с

учетом поправки на % при переходе к шаровой частице с радиусом RS от цилиндрика с таким же радиусом и длиной 2RS (х- длина трубки в направлении движения по оси Х)

3

Умножим и разделим (109) на RS. Учитывая, что mo = 4/3RS •рm, определяем

энергию W1 деформации среды, которую производит передний фронт электрона при своем движении с учетом нормализованного релятивистского фактора yn (70)

W1 = Y nmvCo =Y nmoC2R^

RS

Силу сопротивления F1C, которую оказывает квантованная среда на передний фронт при движении электрона, находим как производную от энергии W1 (110) по направлению х

Балан энергии и компенсация сил (112) обеспечивает движение по инерции. Внешне это наблюдается как процесс, не требующий энергии и сил. Но на самом деле, движение по инерции - это очень энергоемкий (110) и силовой (111) электромагнитный процесс, обеспечивающий обмен реактивной энергии между движущейся частицей (телом) и квантованной средой, поддерживающий волновой перенос массы. Это ответ на вопрос: «Почему частица (тело) движется по инерции?».

При ускорении частицы (тела) баланс энергии и сил (112) нарушается в результате воздействия внешней силы F, которая совершает работу W (75) за вычетом энергии W0 покоя по ускорению частицы (тела), изменяя ее скорость

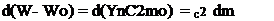
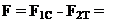
(113)

dx dx dx

Уравнение динамики (113) наиболее объективно отражает физическую сущность ускорения частицы (тела) при воздействии силы F на пути х, как изменение массы dm при ускорении на пути х во всем диапазоне абсолютных скоростей от 0 до Со, где m= ynmo

^ _2 dm

F = C2 —— (114)

dx

Уравнение (114) ранее не применялось в динамике, поскольку ускорение не связывали с увеличением массы, как и торможение с ее уменьшением. Масса в (114) есть величина переменная на пути ускорения х. Если вывести в (114) массу покоя mo из под дифференциала как константу в абсолютном пространстве-времени, то исходя из m= ynmo, получаем

уравнение динамики, в котором переменным параметром выступает только yn

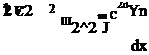В области скоростей v<<C2, порядков

Подставляем (116) в (115), преобразуя константы и умножая левую и правую часть на dt (t - время), получаем

Классическое уравнение динамики (120) не является корректным с физической точки зрения, поскольку масса не является константой, а является величиной переменной, в том числе и в области нерелятивистских скоростей. Но мною специально было подробно показано, что уравнения (119) и (120) получаются из корректного уравнения динамики (114) и (115) при перенормировке массы из переменной величины в константу. Но это чисто математический прием, за которым в основе стоит переменная величина массы. Естественно, что в этом случае, когда масса принимается за константу, компенсацию массы при ее увеличении со скоростью можно производить кинетической энергией (106) и (107).

Теперь, когда вкратце удалось объяснить внутренние процессы динамики частицы (тела) движения в квантованной среде, в том числе по инерции, вернемся к анализу энергетического парадокса, обусловленного тем, что кинетическая энергия может быть определена как выражением (106), так и выражением (107). Как уже отмечалось, движение с ускорением связано с воздействием внешней силы на частицу (тело), которая уравновешена внутренней силой фазового перехода квантовой плотности среды внутри оболочки элементарных частиц, которая ведет к перераспределению концентрации квантонов в направлении движения.

На рис. 14в представлено равномерное распределение квантовой плотности среды p2=C2nst внутри гравитационной границы частицы (тела). Это соответствует состоянию равномерного и прямолинейного движения частицы (тела) по инерции или его покоя (абсолютного или относительного).

На рис. 14а и 14б показаны фазовые переходы квантовой плотности среды в сторону увеличения ее концентрации в области переднего фронта частицы (тела) в направлении движения и в направлении векторов скорости v, ускорения а и силы Fm. Это ведет к

появлению дополнительного вектора деформации D 2 (92)-(93) квантованной среды,

обусловленного ускорением. Сейчас важно понять, что ускорение частицы (тела), помимо изменения сферической деформацией квантованного пространства времени связанного с увеличением скорости, ведет к фазовому переходу квантовой плотности среды внутри
оболочки частицы. Это процесс энергетический и связан с дополнительной работой по ускорению частицы.

Теперь вернемся к понятию инерциальной и неинерциальной систем движения (отсчета). Для инерциальной системы двигающегося по инерции частицы (тела) характерно однородное распределение квантовой плотности внутри оболочки (рис. 14в). Тело состоит из множества частиц и имеет гравитационную границу в квантованной среде, проходящую по поверхности тела. Отличие состоит в том, что квантовая плотность среды внутри гравитационной границы тела определяется усредненной квантовой плотностью среды. Но как только частица (тело) начинает ускоряться, появляются фазовые переходы квантовой плотности среды в направлении ускорения (рис. 14а). Система, двигающаяся с ускорением, является неинерциальной. Таким образом, если частица (тело) двигается с ускорением, а затем ускоряющая сила снимается и тело двигается по инерции, а затем опять с ускорением, то будет наблюдаться переход системы из неинерциальной в инерциальную, а затем опять в неинерциальную. Это формирует характер движения, определяя энергетические затраты активной и реактивной энергий, которые связаны с названными переходами из неинерциальной системы в инерциальную, и наоборот. Потому каждый раз, когда вызываются фазовые переходы квантовой плотности среды, происходит изменение обменных энергетических процессов, обусловленных реактивной компонентой, и изменением полной энергии системы, которые приводят к появлению рассматриваемого энергетического парадокса.

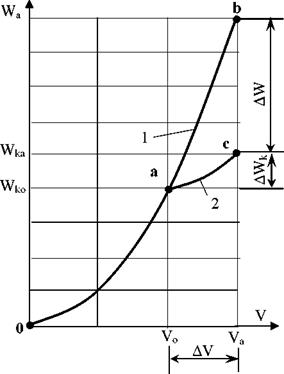Рис. 17. Квадратичные зависимости
абсолютной 1 и относительной 2 энергий
тела (частицы) от скорости v движения в
абсолютном пространстве-времени.
Точка бифуркации - (а).

Объяснение причин энергетического парадокса лучше показать на графике рис. 17, наглядно представляя квадратичные зависимости (106) и (107) кинетической энергии пушечного ядра от скорости v движения. Если бы пушечное ядро ускорялось в абсолютном пространстве-времени с нуля (0) и до абсолютной скорости v, то абсолютная кинетическая энергия ядра Wk1 определялась бы формулой (106), и это полностью соответствовало бы экспериментальным наблюдениям. Но мы не наблюдали ускорение пушечного ядра до скорости v0 на участке (0-а) кривой 1. Это означает, что пушечное ядро, будучи условно когда-то ускорено вместе с пушкой и Землей до скорости v0 претерпело переход из неинерциальной в инерциальную систему. При этом ядро претерпело фазовые переходы квантовой плотности среды в момент ускорения и его снятия. Далее ядро, двигаясь по
инерции с абсолютной скоростью vo в квантованном пространстве времени, не подвергаясь фазовым переходам. В точке (а) произошел выстрел, который еще раз ускорил ядро на величину Av до скорости v. При этом ядро еще раз претерпело фазовые переходы квантовой плотности среды, изменив в точке (а) характер движения, который пошел по кривой 2 в точку (с) с абсолютной кинетической энергией Wka, которая соответствует эксперименту.

По сути дела, точка (а) является точкой бифуркации, раздваивая характер движения ядра в момент фазового перехода квантовой плотности среды, вызванного ускорением в момент выстрела пушки. Точка бифуркации (а) характеризует прерывистость ускорения и переход с движение по инерции. Если бы, повторяю, в точке бифуркации (а) не было бы фазовых переходов квантовой плотности среды, и ядро продолжало бы двигаться с ускорением из точки (0) в точку (b), то абсолютная кинетическая энергия Wk1 при достижении ядром абсолютной скорости v в точке (b) соответствовала бы формуле (106). Получается, что достижение ядром абсолютной скорости v может происходить с различными затратами энергии в зависимости от характера движения и фазовых переходов квантовой плотности среды. Это потрясающий вывод, который обязан принципу относительно-абсолютного дуализма, когда на участке (а-с) характер движения по кривой 2 перешел в точке (а) из абсолютной категории в относительную.

Уменьшение кинетической энергии на разгон тела частицы по кривой (0-а-с) до скорости v (рис. 17) по сравнению с кривой (О-а-b) имеет вполне физическое объяснение. Дело в том, что в точке бифуркации (а) фазовый переход квантовой плотности среды исчезает виду окончания действия ускорения на тело (частицу). Энергия фазового перехода,

обусловленная деформацией D‘2 квантованной среды, сбрасывается в квантованную среду в

результате реактивного обмена энергией без фотонного излучения. Но при этом сохраняется увеличенная энергия сферической деформации среды с внешней стороны. Тело (частица) переходит в состояние рис. 14в без внутреннего напряжения фазового перехода. Последующее ускорение тела (частицы) без внутреннего напряжения фазового перехода производить легче, чем с наличием фазового перехода. Поэтому энергия на разгон тела (частицы) до абсолютной скорости v с наличием точки бифуркации (а) требует меньше энергии на величину на величину mvoAv (108), чем при постоянном и непрерывном ускорении без точки (а). Импульсный разгон элементарной частицы является более экономичным, чем непрерывный.

Необходимо отметить, что в данном случае проявления принципа относительно­абсолютного дуализма обусловлено квадратичными зависимостями кинетической энергии от скорости движения. А вот импульс, то есть количество движения mv пропорционально первой степени от скорости, что упрощает его применение в расчетах по сравнению с кинетической энергией. Можно доказать математически, что любая динамика движения имеет электромагнитную природу в условиях относительно-абсолютного дуализма, в том числе при наличии точки (а) бифуркации на кривой ускорения. С этой целью, преобразуем выражение (107), выделив из него сумму квадратов скоростей

2Wk2 . 2 2

---- — = Av2 + v 2 (121)

m

Очевидно, что величина 2Wk2/m в (121) есть не что иное, как квадрат абсолютной модуля комплексной скорости v2 частицы (тела). Модуль комплексной скорости v отличается от абсолютной скорости v, поскольку представляет собой не сумму скоростей, а связан через сумму квадратов скоростей

v2 = Av2 + v 2 (122)

Из (122) определяем модуль комплексной скорости v

v = ^Av2 + v2 (123)

В комплексной форме абсолютная скорость v описывается общеизвестными

формулами (где i=Vl - мнимая единица, число е=2,71...)

U = Av + ivo = v • e-іф (124)

В (124) вошел угол 9v фазы фазового перехода квантовой плотности среды при ускорении тела (частицы) на величину скорости Av. Угол фазы 9v определяется из формулы Эйлера

Av Av Av/vo

Ф v = arccos— = arccos—^ = arccos— (125)

v

1 +

v

В (128) входит релятивистский фактор у, примененный Эйнштейном в специальной теории относительности (СТО), но который теперь получен исходя из принципа относительно-абсолютного дуализма

1 Со

Y =

v

С2

Преобразуем (129), умножив на массу покоя mo

Со

mo Y = m^- Av

В (130) входит эйнштейновская релятивистская масса m=moy, которая может увеличиваться до бесконечности, при увеличении скорости vo до скорости света Со. Это обусловлено грубым приближением и некорректностью исходной формулы (129) в области релятивистских скоростей. Как уже отмечалось, избавится от бесконечной величины релятивистской массы, удалось в теории УКС и ТЕЭП путем введения нормализованного релятивистского фактора yn (70). Необходимо отметить, что (127) легко преобразуется в четырехмерный интервал, являясь грубым приближением при описании свойств пространства-времени.

В области релятивистских скоростей в случае прямолинейного движения с ускорением в уравнении динамики (120) взамен mo вводится релятивистская масса m= moyn уже с учетом нормализованного релятивистского фактора yn (70)

^ dv,

F = mo Y n (131)

dt

B (131) вектор силы F совпадает с вектором скорости v. В этом случае из (131) получаем релятивистский импульс р для прямолинейного ускорения

р = mo VY n (132)

Выражение (132) позволяет установить предельной значение импульса р^х частицы, которое оно получит при увеличении скорости v от 0 до С0 с учетом (72) и (62) для mo

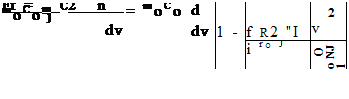В общем случае непрямолинейного движения, когда вектор силы F не совпадает с вектором скорости v релятивистское уравнение динамики (115) можно преобразовать, умножив левую и правую часть на dt как (117)

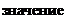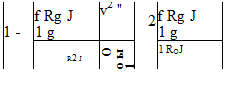
Находим производную от сложной функции (131) и определяем релятивистского импульса во всем диапазоне скоростей от 0 до Со

(135)

Исследования показали, что импульс (135) является поперечным к вектору скорости в отличие от продольного импульса (132). При движении частицы, например, по синусоидальной траектории, общий импульс будет определяться векторной суммой поперечного и продольного импульсов. Импульсу (135) соответствует уравнение динамики с

3.

n.

Таким образом, переход к абсолютному квантованному пространству-времени позволяет довольно просто решать сложные задачи, связанные с определением предельных параметров релятивистских частиц. Зная ускорение частицы в силовом поле, по приведенным выше формулам можно подсчитать время ее разгона. Учитывая, что скорость солнечной системы вместе с Землей значительно меньше скорости света, то можно принять Землю за неподвижный объект, относительно которого ведутся релятивистские измерения параметров частиц в земных условиях. Отрадно то, что полученные уравнения динамики для абсолютного пространства-времени, многие из которых хорошо известны, позволяют перенести их в область относительных измерений. Естественно, будучи ограниченный рамками статьи, отмечу, что данную тему можно развивать до бесконечности.

Но главное, анализ динамики частицы (тела) установил, что непрерывное абсолютное и прерывистое относительные движения отличаются точками бифуркации (а) на кривой разгона рис. 17, обусловленные фазовыми переходами квантовой плотности среды при переходе частицы (тела) в режим из инерциальной системы в неинерциальную, и наоборот. Относительность является фундаментальным свойством квантованного пространства- времени, определяя принцип относительно-абсолютного дуализма. Это подтверждается анализом множества экспериментальных данных. Какой-либо дополнительной проверке принцип относительности не требует. Требуется дальнейшее развитие ужу квантовой теории относительности (КТО) как теории относительных измерений в абсолютном квантованном пространстве-времени в условиях искривления пространства гравитацией.