Исследование закономерностей, количественно определяющих изменение потока радиации при прохождении его через материальную среду, началось задолго до того, как была выяснена природа физических процессов, вызывающих это изменение. Общий закон ослабления света при его прохождении через поглощающую и рассеивающую среду был установлен экспериментально еще в 1729 году французским физиком П. Бугером. С тех пор исследования в данной области продолжались российскими и зарубежными учеными.

Исходными данными для любых оценок распределения солнечной радиации являются данные наблюдений суммарной, рассеянной и прямой радиации на актинометрических станциях, сеть которых на территории России насчитывает более ста сорока пунктов. Используются данные с различным масштабом интегрирования — годовым, месячным, суточным, часовым. Имеются данные различной продолжительности наблюдений — от 30 до 45 лет, за изменениями составляющих коротковолновой солнечной радиации в видимом диапазоне— прямой на перпендикулярную S и горизонтальную площадки, рассеянной D и суммарной 0, а также их экстремальные значения.

Использование солнечной энергии для целей энергетики берут начало с работ Б. П. Вейнберга в 20-е годы, когда на основе обобщения фактических наблюдений и теоретических расчетов был составлен первый солнечный кадастр. Он содержал данные годового и широтного хода возможных месячных и годовых сумм прямой солнечной радиации, поступающей на поверхность перпендикулярную солнечному лучу при условиях ясного неба. Были рассмотрены и приведены также данные о суточном ходе солнечной радиации, продолжительности солнечного сияния для характерных дней года, а также дана карта распределения «технически применимой и экономически выгодной солнечной мощности».

Позднее, в 40-60 годы усилиями СМ. Горленко, И. Н. Ярославцева, Я. А.Цуцкеридзе, О. А. Перовой и других были выполнены кадастровые оценки гелиоэнергетических ресурсов по республикам Средней Азии и Закавказья. Важное дополнение к методикам составления кадастра внес Б. В.Тарнижевский, предложивший учитывать связи метеорологическими факторами и конкретными солнечными энергетическими установками. На основе карт распределения солнечной радиации, построенных Т. Г.Берлянд и Н. А.Ефимовой и моделей работы конкретных солнечных установок им были построены карты распределения годовой и месячной выработки тепловой и электрической энергии по территории юга страны. Вместе с тем выполненные работы в большинстве случаев недостаточно учитывали вероятностную природу поступления солнечной энергии, так как были построены на осредненных и суммарных значениях характеристик радиации и продолжительности солнечного сияния.

Как показали проблемы определения показателей солнечных установок данных, полученных на основе таких кадастров, недостаточно. Качественньш шагом вперед в деле создания современного солнечного кадастра явились более поздние работы Т. Г. Берлянд, Г. А. Гриневича, Н. В. Кобышевой, Г. Я. Наровлянского, З. И. Пивоваровой, Р. Б. Салиевой, В. В. Стадник и др., а также Дж. А. Даффи, У. А. Бекмана, Ст. Лингова, Л. Махта и др. В этих работах рассмотрены принципы разработки солнечного кадастра как совокупности объективных численных характеристик, описывающих закономерно-стохастические процессы и учитывающих вероятностную структуру и пространственно-временную динамику поступления солнечной радиации и метеопараметров. Расчет таких характеристик по данным фактических наблюдений служат основой для построения математической модели. Правильньш выбор модели позволяет прогнозировать природный режим поступления солнечной радиации к земной поверхности на предстоящий период. Прогноз солнечной радиации должен стать в гелиоэнергетике таким же привычным как прогноз погоды.

На текущий момент существует несколько методик для расчета плотности СИ при чистом небе, базирующиеся на эмпирических выражениях, которые характеризуют влияние атмосферы на прохождение солнечного излучения, разработанные преимущественно зарубежными авторами. Такие методы обладают рядом недостатков, к которым следует отнести относительно невысокую точность полученных данных, невозможность проведения окончательных расчетов без использования дополнительной информации по месячным или среднемесячным дневным суммам солнечного излучения при реальном состоянии атмосферы. Однако можно отметить и существенные достоинства расчетных методов, к числу которых относятся:

1. минимальный набор используемых исходных данных (географические координаты, месячные или среднемесячные дневные суммы солнечной радиации для заданного места);

2. возможность получения реальных почасовых значений прихода солнечного излучения для любого дня года;

3. возможность расчета почасовых значений солнечного излучения, поступающего на поверхность солнечной энергоустановки, ориентированную произвольным образом;

4. простота и высокая оперативность определения данных при предварительном проектировании солнечных энергоустановок.

На кафедре ВИЭГ СПбГПУ под руководством В. А. Грилихеса был проведен анализ основных разработанных в мире методик расчета поступления СИ и сделан вывод, что при проектировании солнечных установок, целесообразно использовать методику Бёрда, с поправочными коэффициентами, учитывающими особенности реальной плотности энергии падающей солнечной радиации на территории России. Для прямого СИ, падающего на горизонтальную поверхность, значения поправочных коэффициентов для территории

бывшего СССР приняты равными К^ист = 1,14 для зимних месяцев

и K*Jo0tcm — 0,91 для летних месяцев года. При расчете диффузного

у л

СИ, поступающего на горизонтальную поверхность, для всех месяцев года принят единый коэффициент, равный К^рчист -1,05.

С учетом поправочных коэффициентов зависимости для расчета плотности солнечного излучения при чистом небе на горизонтальной поверхности имеют вид:

Для прямого СИ:

Ег°Рр{п, і) = Ес -cos©2(w, • rf - Кпр (з.8)

ї

Для диффузного СИ:

Е7Щп,{) = Ес • C°S0Z(«,0■ Т^ф(п,1) ■ Кдиф (3 9)

9

где п — номер дня в году, начиная с 1 января, / — расчетное время, Ес =1360 Вт/м2— нормальная плотность солнечной радиации в космосе, ©Zf— текущий угол падения лучей на горизонтальную

поверхность, т£р — коэффициент пропускания, солнечного излучения в чистой атмосфере, Кпр — поправочный коэффициент

для расчета прямого СИ, падающего на следящую поверхность, действительный при расчете радиации на территории России.

Косинус угла падения определяется по формуле: cos &2 («, /) = cos 5С(л) cos<рм cos сос(п9/) + sin (рм • sin 5С (п),

w — 81

где <5с(л) = 23.45° sm(36Q0 --------------- )— угол склонения Солнца в

365

расчетный день каждого месяца; п — порядковый номер дня года,

15°

начиная с 1 января; тс(л, t) = — ^ (я, /) -12 — часовой угол

ч

Солнца ддя каждого часа; tc(n, t) — истинное солнечное время, (рм — широта местности.

Входящие в выражение (3.8-3.9) коэффициенты пропускания прямого солнечного излучения в чистой атмосфере определяются по следующим эмпирическим зависимостям:

rf (и,0 = TR( n, t)■ T0J (n, t)• Tgaz(n, t)• тИ2о(п, і)■ TA(n, t)

(«10 = Го30М)‘ Tgaz («. 0 • («»0 • Taa («. 0 *

<-*'(«,0+ «'(«,0L02J

где:

,, /•„ А ~„п4_10.873 4,„ I _ ,0.7088 а0-9108

га(н,0 = ехр%гл Л+ - гй

> 

где та' = .832р, а р = 0.0314 - коэффициент спектральной мутности Ангстрема.

- коэффициент пропускания, учитывающий поглощение СИ озоном:

1 + 0.044/oj • /и'(иД) + 0.0003^ ’7И'(Л,03 где d0^— ширина озонового слоя в см. при нормальной температуре и давлении (для средних широт d03 ~ 0,32 см )

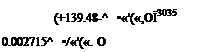- коэффициент пропускания, учитывающий поглощение СИ

газовой смесью:

Tgaz(n, t) =ехр(-0.0127./ф,00-26)

-коэффициент пропускания, учитывающий поглощение СИ водяным паром:

2.4959 • deip

Т"2° ~1~(+79.034 • */*да'(л>28 + 6.385 • d где — показатель содержания пара в вертикальном столбе

атмосферы измеряемый в г/см2. Для средних широт

d =1,3ч-3г/см2 в зависимости от времени года (зимой —1,3,

н^о

летом ~3, весной и осенью -2)

- коэффициент пропускания, учитывающий поглощение СИ частицами аэрозоля:

Тва = 1 - ОД С - пі (и, 0 + пі (п, О1,06 J, i-Ta (и, /)

-

коэффициент пропускания, учитывающий рассеяние СИ частицами аэрозоля:

Ba(n, t) — отношение рассеянного прямого излучения к общему рассеянному излучению. Для сельской местности Ва =0,82, в общем случае определяется по формуле Ba(n, t) = 0,5<+cos©z(/7,f)
скорректированная по высоте местности над уровнем моря, атмосферная масса.

Плотность полного солнечного излучения определяется как сумма прямого и диффузного СИ:

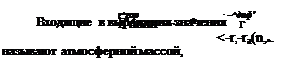где значение альбедо атмосферы определяется по следующей формуле:

га (”> О ~0,0685 + <-£„(/?,/))-гат (и,

/?5 — значение коэффициента отражения или альбедо земной

поверхности представлено в таблице 3.1.

Таблица 3.1. Значение альбедо подстилающей поверхности Снег свежий 0,75-0,95 Трава 0,2-0,3 Снег старый 0,4-0,6 Зеленый лес 0,1-0,2 Пустыня 0,3-0,4 Сухой лес 0,1-0,15 Почва сухая 0Л 5-0,3 Бетон 0,25-0,35 Почва мокрая 0,1-0,2 Асфальт 0,1-0,2

Поступление энергии СИ на горизонтальную поверхность в течении для п вычисляется как:

<зсхМ

Ж„7(«)= j (/, , (ЗЛІ)

»S(")= J (З-12)

где > !3axW — местное время восхода и захода солнца.

Аналогичным образом определяется поступление СИ на горизонтальную поверхность в течении месяца і

К7&= I Kpwdn>

нач

rtj

И%£(0= і w^{n)dn,

..нач

где п]а, nj" — номера начального и конечного дней месяца /.

Тогда полное поступление СИ при чистой атмосфере на горизонтальную поверхность в течении месяца і составит:

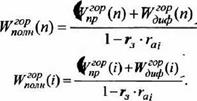(3.15)

(3.16)

Вышеописанная методика описывает поступление солнечной радиации на горизонтально ориентированную поверхность при чистом небе, не учитывая местные особенности, такие как облачность, загрязненность воздуха промышленными газами и другие техногенные факторы. Для учета поступления СИ в реальных климатических и техногенных условиях используется метод определения реальных часовых сумм плотности энергии СИ по известным часовым суммам плотности энергии СИ для ясного неба предложенный В. А. Грилихесом.

Расчет поступления СИ в реальных условиях облачности включает два этапа:

1. Определение коэффициентов пересчета для реальных условий облачности

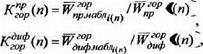(ЗЛ7)

(3.18)

где, ^дифнабл среднемесячные ДНЄВНЬІЄ СуММЫ ПрЯМОШ И

диффузного СИ, наблюдаемые на станции; W™p (/), (і)—

рассчитанные среднемесячные дневные суммы прямого и диффузного СИ, падающего на горизонтальную поверхность, /(я) — номер месяца рассматриваемого дня.

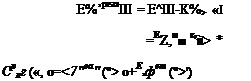2. Расчет реальных часовых значений плотности энергии СИ, поступающего на горизонтальную поверхность:

3.3, ОСНОВНЫЕ ЭНЕРГЕТИЧЕСКИЕ ПАРАМЕТРЫ УСТАНОВОК, ИСПОЛЬЗУЮЩИХ ВОЗОБНОВЛЯЕМЫЕ ВИДЫ ЭНЕРГИИ

Основными энергетическими параметрами установок на основе ВИЭ, имеющими наиболее существенное значение для потребителя, являются: установленная мощность станции (установки) 7VycT и объем произведенной энергии за год Эг. При обосновании и проектировании энергетических установок, использующих ВИЭ кроме отмеченных, необходимы показатели, определяющие режимы работы энергоустановки, характеристики прихода энергии, характеристики рельефа и подстилающей поверхности местности, параметры воздействия на окружающую среду.

Определение основных энергетических параметров гидроэлектростанций.

Для работы гидроэлектростанции необходим расход воды Q и перепад уровней, т. е. напор Н. Полностью использовать мощность водотока на ГЭС невозможно, она будет меньше за счет гидравлических потерь энергии в подводящих и отводящих

сооружениях, потерь в самих турбинах, а также потерь энергии при трансформации механической энергии вращения вала в

электрическую энергии в генераторе.

В главе 2 были рассмотрены три основные схемы использования водной энергии: плотинная, деривационная и плотинно­

деривационная. Создаваемый в этих схемах напор, равный разности отметок уровней верхнего VBE и нижнего УНБ бьефов называется геометрическим или статическим напором Нст.

Нст=УВБ-ЧНБ

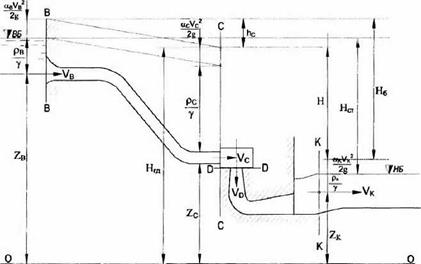
Рассмотрим движение воды в водопроводящем тракте гидроэлектростанции (рис. 3.7). Из основного закона механики жидкости, описанного уравнением Бернулли, следует, что удельную полную энергию потока или гидродинамический напор НГд в любом сечении потока можно представить в виде:

£ = tfra=Z + —(3.22) Д 2

где Р - избыточное давление, Па; р - плотность жидкости, кг/м3; g - ускорение свободного падения, м/с2; Z - геометрическая высота расположения центра тяжести данного живого сечения потока над плоскостью сравнения О-О, м; v - средняя скорость течения воды в данном живом ссчснии, м/с; а - коэффициент Кориолиса или коэффициент кинетической энергии (величина этого коэффициента зависит от формы эпюры скорости). Все члены данного уравнения имеют линейную размерность и несут энергетический смысл.

Величина Z представляет собой удельную потенциальную

Р

энергию положения единицы веса жидкости,------------------------- удельную

pg

потенциальную энергию давления. Эти два слагаемых создают

Р

потенциальный напор Hn=Z 4- — т. е. удельную потенциальную

Pg

энергию единицы веса жидкости в одном живом сечении относительно плоскости сравнения.

у

Третье слагаемое уравнения (3.22), а------------------------- скоростной

2 g

(кинетический) напор, представляет собой удельную кинетическую энергию.

Рис. 3.7. Схема к определению параметров ГЭС Полный напор ГЭС определяется как разность удельных энергий потока воды во входном сечении водопроводящего тракта В - В и в его конечном сечении К-К (см. рис.3.7). Полный напор также называют напором брутто Нб или напором гидротурбинного блока:

H6=EB-EK=ZB-ZK + - п ~Рк + ?*** ~ (3.23)

Pg 2 g

т. е. вся энергия потока в водопроводящем тракте складывается из

р _р

энергии положения ZB-ZK, энергии давления —--------------------------- — и

Pg

„ ОС и

кинетической энергии ---------------- .

2 g

Энергия, получаемая рабочим колесом от водного потока, будет равна разности удельных энергий на входе в рабочее колеса С-С и на выходе из него К-К. Эта величина представляет собой рабочий напор турбины Н, Он меньше напора брутто на величину гидравлических

h

потерь в водопроводящем тракте с, вызванных действием в потоке сил сопротивления. Данная величина выражает усредненную потерю удельной механической энергии между сечениями В-В и С-С и состоит из гидравлических потерь на трение (по длине водопроводящего тракта) и местных потерь. Следовательно, рабочий напор будет равен Н =H6-hc. р

Сумма Z + — = V, дает отметку уровня воды соответственно в PS

Р Р

сечениях В-В и К-К, т.е. ZB + — - S'ВБ V, ZK + — = УНБ V

PS PS

С учетом (3.22) и (3.23) рабочий напор составит:

Я = + (3.24)

2S.

Скорость воды перед водоприемником и в выходном сечении нижнего бьефа невелики и разностью кинетических энергий в этих сечениях для практических расчетов можно пренебречь. Тогда, для практических расчетов рабочий или полезный напор турбины выражают формулой:

Я = Яст-Лс

Рассмотрим теперь движение потока только через рабочее колесо турбины. Удельная энергия, отданная потоком непосредственно рабочему колесу, будет равна разности удельных энергий перед рабочим колесом (сечение С-С) и на выходе из него (сечение Д-Д), на рис. 3.4.

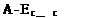
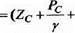) “ (Zd + ~ +

r

Гидравлическая энергия, преобразуемая в турбине в механическую, состоит из потенциальной части

Ап ~~С + ZC -ZD

Г

и кинетической

_ &CVC ~ aDvD к~ 2£

В зависимости от того, какие основные виды энергии преобразуется на рабочем колесе, турбины делятся на реактивные и активные.

Расход воды Q, м3/с, пропускаемый турбиной, используется на ГЭС для выработки электроэнергии. Он зависит от притока воды к верхнему бьефу ГЭС, наличия запасов воды в водохранилище и потребности в мощности и выработке электрической энергии потребителей. Максимальный расход ГЭС равен пропускной способности всех турбин при расчетном напоре.

Для малых, мини и микро-ГЭС, оснащенных нерегулируемыми реактивными турбинами, расход воды, протекающий через них, зависит от рабочего напора Я и может быть представлен в виде следующий расчетной зависимости:

Q = /jTcoj2gH

> 

где а) - площадь камеры рабочего колеса.

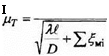Коэффициент (Гг — коэффициент расхода подводящего трубопровода.

где X — коэффициент трения, ^ и D - длина и диаметр подводящего трубопровода, — коэффициенты местных сопротивлений.

Мощность турбины. Мощность потока воды Я0, кВт, проходящего через водопроводящий тракт турбину, при полезном напоре Я, м, определяют по формуле

где Q - расход воды через турбину, mVc.

В блоке ГЭС не вся мощность используется полезно. Преобразование гидравлической энергии в механическую происходит с потерями, поэтому мощность на валу турбины Nm будет меньше мощности TVo.

Потери в самой турбине учитываются коэффициентом полезного действия (к. п.д.) турбины rjm

N

rjm = —L~

Щ

?

где rjm = rj2rf0rjM — полный к. п.д. турбины, представляющий собой произведение частных к. п.д. — гидравлического, объемного и механического.

Следовательно, мощность турбины составит

Nm=g-Q'H-rrM.

Значение к. п.д. турбины зависит от ее конструкции, размеров и изменяется при изменении нагрузки. Электрическая мощность гидроагрегата Nea на выводах генератора меньше мощности турбины на величину потерь в генераторе:

(3.26)

где Пген — к-п. д. генератора; г]га=т]т- — к. п.д. гидроагрегата.

Номинальной мощностью гидроагрегата называется наибольшая активная мощность генератора, которую он может развивать при расчетном значении коэффициента мощности cosp. Эта мощность указывается в паспорте генератора.

Энергия выработанная турбиной Эт выражается произведением 3m=Nm-t, где t - время, с или ч. Энергия измеряется в джоулях и ее производных, причем 1 Дж=1Н*м=1Вт*с.

В энергетике наибольшее распространение получило измерение энергии в киловатт-часах. Известно, что 1 кВт-ч=3600 Дж.

Объем годового стока реки W, м3, используемого ГЭС при напоре Н9 м, дает количество энергии, выработанной ГЭС за год

Y = g 'W Н - г/д, [кДж] или Y = ^ [кВт-ч]. (3.27)

367

Если при ГЭС сооружаемой на реке, создается водохранилище, то обеспечивается возможность перераспределения речного стока и объем выработки энергии ГЭС определяется с учетом полезного объема водохранилища.

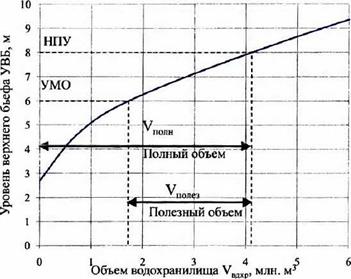
Отметка уровня верхнего бьефа УВБ и объем водохранилища связаны зависимостью ^/(УВБ), вид которой представлен на рис. 3.8.

Рис. 3.8. Зависимости объема водохранилища от уровня воды

Характерные уровни верхнего бьефа — нормальный подпорный НПУ и мертвого объема УМО, которым соответствуют полный и мертвый объемы водохранилища. Разница между последними определяет полезный объем

~ Vнпу ~ Уумо л

Расход ГЭС, или зарегулированный расход, определяется видом регулирования стока реки с помощью водохранилища. Длительное регулирование (годичное, многолетнее) производится с целью выравнивания неравномерности речного стока в разрезе года или ряда лет. Краткосрочное (недельное или суточное) регулирование осуществляется для перерегулирования равномерного недельного или суточного расхода воды в реке в соответствии с неравномерностью потребления энергии в течение недели или суток различными потребителями.

Определение основных энергетических параметров ветроэнергетических установок.

Для ветроэнергетических установок важнейшими параметрами являются: мощность ВЭУ, диаметр ротора ветроколеса, коэффициент использования мощности, тип и параметры генератора и рабочая характеристика ВЭУ.

Важным показателем является коэффициент использования мощности кис„. Строго говоря, коэффициент использования (кисп) должен учитывать также простой ВЭУ по техническим причинам — профилактика, ремонты, которые несколько снижают величину кис„. Однако, если техническое обслуживание ВЭУ проводится в периоды штилей и энергетических затиший, когда скорость ветра и<оо, то снижение величины кис» по техническим причинам можно ожидать незначительным, поэтому в настоящее время пользуются кисп.

Для выполнения расчета обеспеченности мощности ветроагрегатов необходимы рабочая характеристика ВЭУ и распределение скорости ветра на высоте оси ротора.

Энергию ветрового потока можно подсчитать, если воспользоваться выражением для кинетической энергии тела массой т, движущегося со скоростью v. Подставив массу воздушного потока, заключенную в объеме W9 получим:

V2 V2

E = m-— = p-W - — ,

где р - плотность воздуха.

Тогда мощность ветрового потока, т. е, энергия в единицу времени t, проходящего через площадь F с расходом Q, будет равна

у2 у3

7Vn = р Q*/--------- = p-F-------- .

п 2-t 2

Мощность ветроагрегата отличается от мощности ветрового потока, проходящего через ветроколесо, коэффициентом использования ветровой энергией С:

Nb=C-p-Fc - — 9

где FB - ометаемая площадь ветроколеса ВЭУ. Величина С определяется произведением:

С - Ск ■ 7г ' ^м: 5

где Ск - коэффициент использования энергии ветрового потока ветроколесом; rjv и tjM - коэффициенты полезного действия соответственно генератора и мультипликатора.

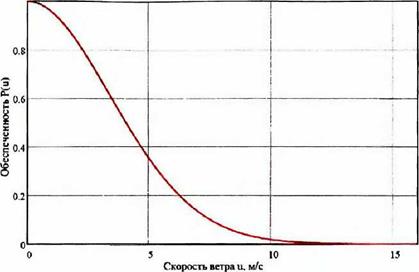
Для подсчета мощности и выработки энергии ветроагрегатом используются данные наблюдений за скоростями ветра, имеющиеся в местных центрах гидрометеорологических наблюдений. Эти данные могут быть пересчитаны и представлены в виде кривой обеспеченности. Пример представлен нарис. 3.9.

Используя формулу, приведенную выше, подсчитывают мощности ветрового потока и строят график обеспеченности его мощности. Площадь графика представляет собой годовую энергию ветра.

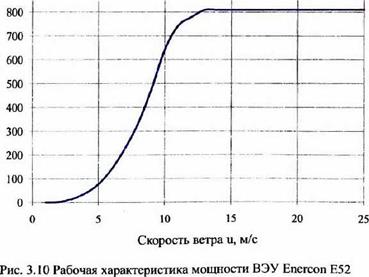
При определении основных энергетических параметров определенного ВЭУ кроме ветровых данных о ветропотенциале необходима рабочая характеристика этого ветроагрегата. Общий вид характеристик представлен на рис. ЗЛО. Из них видно, что различные типы ВЭУ имеют разные мощности, а кроме того, ветроагрегаты отличаются начальной, номинальной и максимальной скоростями ветра.

Рис. 3.9 Кривая обеспеченности скорости ветра

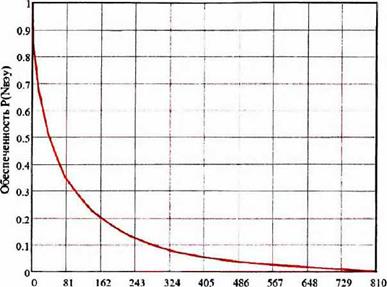
По кривой обеспеченности ветра для данной местности и рабочей характеристике конкретного ВЭУ, рассчитывают график обеспеченности мощности этого ветроагрегата (рис. 3.11). Мощность ВЭУ N»3y, КВт Рис. 3.11 Кривая обеспеченности мощности ВЭУ Enercon Е52 Площадь под графиком определит величину среднегодовой выработки электроэнергии Эвэу Таким образом:

і

*ay6 =8760pV(P)rf/>.

О

На выработку электроэнергии ветроагрегатами, а следовательно, и на их экономическую эффективность, существенное влияние оказывают:

- ветровые характеристики местности;

- применяемый тип ВЭУ и его конструктивное исполнение;

- рабочая характеристика ветроагрегата;

- используемое электрическое оборудование ВЭУ.

Определение параметров солнечных энергоустановок Фотоэлектрические преобразователи солнечной энергии представляют из себя фотоэлементы, действие которых основано на фотоэффекте в полупроводниковых структурах с р-n переходами, где происходит непосредственное преобразование солнечного света в электрический ток.

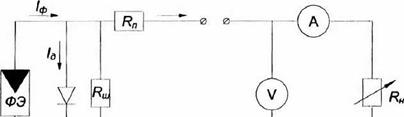
Эквивалентная схема солнечной батареи, как источника электропитания может быть представлена в виде, показанном на рис. 3.12.

Рис. 3.12 Эквивалентная схема солнечной батареи и нагрузки В работах Н. С. Лидоренко, Ж. И Алферова, В. М Андреева, В. А. Грилихеса, М. М Колтуна, В. Д Румянцева, М. Б Кагана и др., посвященных теории и экспериментальному исследованию свойств солнечных элементов (СЭ) показано, что вольтамперная характеристика (ВАХ) СЭ отличается от ВАХ полупроводникового диода появлением члена Ц, обозначающего собой ток, генерируемый элементом под действием освещения, часть которого 1дь течет через диод, а другая — через нагрузку:

qU

где 1ф=1а(екТ -1), 10— обратный ток насыщения; q— заряд

электрона; Т— абсолютная температура; к— постоянная Больцмана; U — напряжение.

Для реального солнечного элемента характерно наличие последовательного сопротивления контактных слоёв Rn. Учет этого сопротивления и введения коэффициента А, отражающего степень приближения параметров реального элемента к характеристикам идеального, после некоторых преобразований получаем:

где A — коэффициент приближения реального элемента к идеальному, К— постоянная Стефана-Больцмана, Т— абсолютная температура, q — заряд электрона, Ц — ток, генерируемый фотоэлементом, /— ток, протекающий через нагрузку Rn, h — обратный ток через р - п переход.

При режиме холостого хода, т. е. при 1И =0, Rn = оо, U = Vja9 а при (7 = 0, т. е. при режиме короткого замыкания IH = 1КЗ, Rn = 0

Оптимальная выходная мощность элемента, снимаемая с 1 см2 площади элемента, может быть оценена из соотношения:

^onm ~ (Jh * ^ФЭП )тах — І' ^ кз ' ^кз >

где £— коэффициент заполнения вольтамперной характеристики, показывающий степень приближения формы характеристики к прямоугольной. У лучших фотоэлементов £=0,8-0,9, обычно £=0,75-0,8.

Ток и напряжение фотоэлемента зависит от температуры фотоэлемента и интенсивности солнечного излучения. Зная эталонные (как правило паспортные) характеристики элемента — ток 1Э и напряжение U3 при эталонных интенсивности Еэ (обычно 1000 Вт/м2) и температуре Тэ (обычно 25°С).

Текущие значения тока и напряжения будут можно вычислить по следующим формулам:

Еэ

Э

и^к = из-Ки(Т-Т3),

где, Kf, Ки — температурные коэффициента тока напряжения.

Коэффициент полезного действия солнечного элемента в основном зависит от температуры, которая может достигать больших значений при использовании фокусирующих систем или при работе в космическом пространстве. В наземных условиях и при применен™ бесконцентраторных фотоэлектрических панелей температура элемента изменяется в небольшом диапазоне, что не существенно влияет на его КПД. Однако, например в условиях жаркого климата (в Африке, Индии и др. приэкваториальных странах) температура может сильно отличаться от эталонных. В этом случае КПД солнечного элемента может быть определен по формуле:

^=^г(і-д(7;-rr)f

где Тг— эталонная температура СЭ; Тс—текущая температура СЭ; jfr —эталонный КПД СЭ; А — температурный коэффициент (для кремния может быть принят равным 45*10-4 ,°С). Вид вольтамперных характеристик при различных значениях интенсивности приведен на рис. 3.13, а. Влияние температурной деградации солнечного элемента приводит к снижению к. п.д. элемента, так же как и изменение интенсивности излучения относительно эталонных значений. На рис. 3.13, б, в представлена зависимость f]=f(T) для кремниевых и арсенидо-галиевых элементов.

При объединении элементов в батарею, имеющую п параллельных рядов, в каждом из которых объединены последовательно m элементов, выходные напряжение и ток системы составят соответственно UebIX =UG 1вых =10-п.

К. п.д. солнечного элемента площадью FC3 определяется по формуле:

Р

л опт

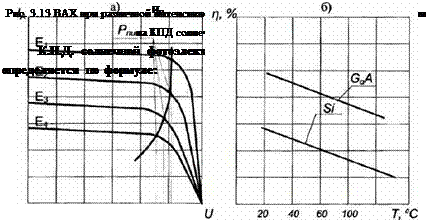Значения достигнутых в настоящее время к. п.д, солнечных элементов различных типов приведены на рис. 2.19.

Рщ,

EyFoYA

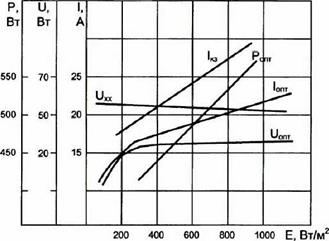
Работа солнечных батарей в наземных условиях происходит при переменной плотности радиации, поступление которой определяется суточным ходом, метеоусловиями прозрачностью атмосферы. Отметим, что изменение мощности батареи происходит в основном за счет изменения тока солнечной батареи. Анализируя зависимости основных параметров СБ от уровня радиации рис. 3.14, можно установить, что с ростом интенсивности солнечных лучей, падающих на её поверхность, линейно растут ток /„ и мощность P0„nJt при этом напряжение Uonm изменяется в узком пределе изменения интенсивности. Однако этот закон сохраняется лишь при сравнительно высоких значениях Е, в противном случае, при низких

Е (Е < 100 Вт/м2) напряжение Цопт резко падает до нулевого значения (как и остальные параметры СБ). В связи с этим при прямом подключении СБ к потребителю могут возникнуть перепады мощности, что является нежелательным, поэтому при расчетах вводится ограничение по минимальному уровню интенсивности, при котором еще возможно нормальное функционирование СБ и всей системы в целом.

Рис. 3.14 Зависимость основных параметров ФЭП от уровня радиации Определение параметров теплового коллектора солнечной энергии. Выполнение теплового расчета коллектора и солнечной системы теплоснабжения в целом представляет определенные трудности из-за необходимости учета влияния случайных колебаний климатических параметров и сложного характера взаимодействия между элементами системы. Поэтому обычно используются инженерные методы, которые дают возможность получить приемлемые характеристики проектируемой системы. Упрощенный метод расчета солнечной установки отопления и горячего водоснабжения здания заключается в определении, прежде всего, площади поверхности коллектора солнечной энергии SCK

Тепловая мощность (Вт) плоского коллектора солнечной энергии (КСЭ) определяется как:

Qk =$ск ЪпЛ'о~К'кФт - Тт2)

»

где SCK.— площадь поверхности КСЭ, м2; Еп — плотность потока солнечной радиации, поступающей на поверхность коллектора, Вт/м2; rj'0 — эффективный оптический КПД коллектора; К'к — общий коэффициент тепловых потерь коллектора, Вт/(м2,К); Тт и Тт2 — температура теплоносителя на входе в КСЭ и на выходе из него, °С; G — массовый расход теплоносителя в КСЭ, кг/с; ср —

удельная изобарная теплоемкость теплоносителя, Дж/(кг-°С).

Удельная среднемесячная дневная теплопроизводительность коллектора солнечной энергии, МДж/м3 в день вычисляется по формуле:

qe=Wrf0Q-a-P + b-P)

7

где Wd — среднемесячное дневное количество солнечной энергии поступающей на 1 м2 площади поверхности КСЭ, МДж/м2 в день.

Метод расчета величины W6 описан в §3.2. Коэффициенты aub приведены в таблице 3.2 для плоских типов КСЭ, используемых в солнечных установках теплоснабжения.

равный отношению среднемесячных значений солнечной радиации, поступающих за день на горизонтальную поверхность на земле и за пределами земной атмосферы.

На теплопроизводительность коллектора солнечной энергии (КСЭ) в данных климатических условиях сильно влияет температура Т

теплоносителя на входе в КСЭ. Так, при годовом суммарном поступлении солнечной энергии на плоскость КСЭ 4060 МДж/м2 (в
том числе 1880МДж/м2 диффузного солнечного излучения) на 47°с. ш.} годовая теплопроизводительность q™d КСЭ с ifa = 0,73 и

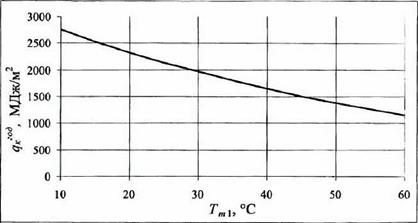
К'к - 4,5 Вт/(м2*К) и углом наклона р=50° изменяется в зависимости от температуры теплоносителя на входе в КСЭ ТтХ следующим образом (рис, 3.15):

Рис. 3.15 Зависимость годовой теплопроизводителыюсти от температуры теплоносителя на входе в плоский КСЭ

Таблица 3.2 Осредненные коэффициенты а и Ь для плоских типов КСЭ Типы КСЭ Чо К 8*10’ Ь*10й НПК - 1 0,78 8,0 10,7 29,3 НПК-2 0,73 4,6 6,9 12,7 СПК - 1 0,75 5,5 7,9 16,4 СПК - 2 0,7 3,5 5,6 8,7 '

Примечание: НПК — неселективный плоский коллектор:

СПК— селективный плоский коллектор; I - 2 - число слоев остекления.

4. АККУМУЛИРОВАНИЕ ЭНЕРГИИ ВОЗОБНОВЛЯЕМЫХ ИСТОЧНИКОВ

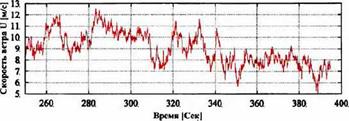
Важнейшим вопросом, который необходимо решить для широкого использования возобновляемых источников энергии (ВИЭ) является вопрос эффективного перераспределения получаемой от возобновляемых источников энергии во времени. Как известно приход энергии ВИЭ является весьма неравномерным и зависящим от многих факторов (Рис. 4.1) Одновременно и процесс потребления или график нагрузки также неравномерен в зависимости от ритма жизни человека, характера потребления и т. д.

Рис.4.1 Изменение скорости ветра в краткосрочных интервалах времени Для согласования этих процессов возможно использование следующих режимов работы установки на ВИЭ: - работа в энергосистеме параллельно с сетью в режиме максимума выработки; - недоиспользование энергии возобновляемых источников путем диссипации лишней энергии; - подстраивание процесса потребления под процесс производства; - комбинированное использование нескольких источников возобновляемой энергии, обеспечивающих требуемый режим потребления; - накопление излишков энергии в периоды максимума прихода ВИЭ и отдача в периоды минимумов, т. е. аккумулирование.

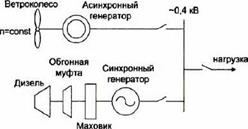
Первый режим работы реализован в настоящее время, например на ветродизельных электростанциях (рис. 4.2), а также на крупных сетевых солнечных и ветровых электростанциях (рис. 4.3). Этот режим не требует специальных устройств аккумулирования, так как все процессы согласования нагрузок обеспечивают другие электростанции.

Рис. 4.2 Схема автономной системы энергоснабжения с ветроагрегатом и дизель-генератором

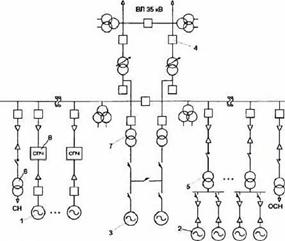
Рис. 4.3 Схема ВЭС, работающей параллельно с сетью: 1 и 2 - ВЭУ; 3 - аварийные дизель-генераторы; 4 - повышающие трансформаторы; 5 и 7 - трансформаторы 0.4/10.0 кВ; 6 - трансформаторы собственных нужд; 8 - статический преобразователь

Остальные режимы работы более характерны для небольших и изолированных энергосистем, когда процесс регулирования мощности должны осуществлять сами установки на ВИЗ или системы интегрированные с ними.

Режим недоиспользования энергии может оказаться самым простым, но он потребует, во-первых значительного превышения установленной мощности установки над требуемой нагрузкой и во - вторых было бы расточительно безвозвратно терять уже произведенную энергию. Примером такого режима может служить установка с балластным сопротивлением (рис. 4.4).

Режим подстраивания потребления энергии под производство снижает комфортность проживания человека, заставляет секционировать нагрузку, пребывать в режиме ожидания отключения.

Рис. 4.4 Схема работы ВЭУ с балластным сопротивлением Четвертый и пятый режимы в наибольшей степени удовлетворяют требованиям качества энергоснабжения.