The net power input for the weld, volt x amp x efficiency/speed, should equal the total thermal load reaction or sum of the Lagrange multipliers at the nodes connected to the prescribed temperature field in the weld pool. This is a consistency check and a redundant measure of correctness.

Since the total heat input is determined only by the temperature field at the liquid-solid boundary, i. e., q = - к Tn, the net power input can be achieved by adjusting the weld pool size. The power input does not depend on the temperature of the interior of the weld pool even if the weld pool is a cavity. In a weld with a double pool, the metal in the leading pool is usually blown away in a real weld. In the model, the absence of molten metal in the cavity can be ignored without penalty.

If the region near the arc is studied in detail, then the double ellipsoid model for prescribing the heat input may be better [3]. This should then be combined with a fine mesh with about 10 linear elements across the axis of the ellipsoid area of heat input [3 and 8]. The heat input can be adjusted to fit the experimental data. This can be for example the fusion zone, but the highest accuracy can be obtained when transient temperatures have been measured.

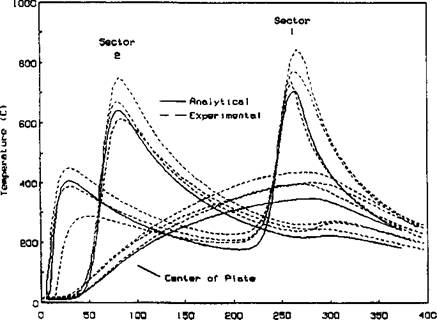
Jones et al. [9 and 10] prescribed the temperature at the boundary of the weld pool which was defined before hand by the user to be equal to the Tuquidus - They simulated the welding of a bead on a disc and compared temperatures with measured temperatures and obtained quite good agreement. Figure 3-3 compares measured temperatures at some different locations with computed values.

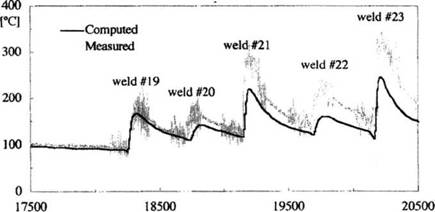
It is not difficult to achieve good accuracy for the temperatures at some distance from the weld, especially if only a few weld passes are made [3]. The problem of matching measured temperatures is naturally greater when the measurement is performed closer to the arc. Figure 3-4 shows that the agreement is quite good at weld 19 when the thermocouple is farther away from the arc but not so good during later weld passes when the arc comes closer to the thermocouple.

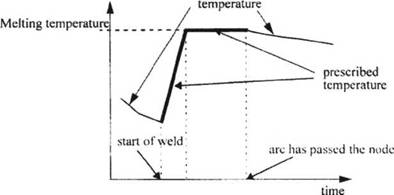
Roelens [11 and 12] and Lindgren et al. [3 and 13] prescribed the temperature in the case of multi pass welds. The temperature for a weld pass is specified during the heat input phase, as shown in Figure 3-5. Results from this technique for a 28-multipass weld are shown in Figure 3-4.

The temperature levels in the neighborhood of the peak temperature may be more important to match than the peak itself. Then the correct total amount of net heat input is obtained. Since the weld pool has dimensions of the order of a cm and the structure usually has dimensions of the order of 10s of cm, the mesh must be graded to reduce computational costs to affordable levels.