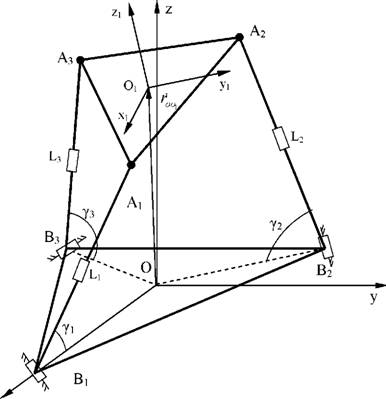
Рассмотрим виброизоляционную систему на основе механизма с тремя степенями свободы и параллельной ки­нематикой трипода, который состоит из основания B1B2B3, подвижной платфор­мы A1A2A3, трех штанг переменной дли­ны L1 - L3, каждая из которых состоит из двух стержней и активной поступатель­ной кинематической пары (рис. 1).

На рисунке приняты следующие обозначения:

Oxyz - глобальная система коорди­нат; B1, B2, B3 - цилиндрические шарни­ры; A1, A2, A3 - сферические шарниры; L1, L2, L3 - поступательные кинематиче­ские пары.

Определим радиус-векторы точек платформы B1B2B3 как векторную сумму:

RA1 = Г001 ^ rO1A1 ,

ГА2 = Г001 ^ Г01А2 , (2)

ГА3 = Г001 ^ Г01А3 .

Исходя из геометрических соотно­шений, составим уравнения связи для платформы А1А2А3:

(x - x2)2 + (У1 - У2)2 + (Z1 - Z2)2 = AA32,

(x2 - x^)2 + (У2 - У3)2 + (Z2 - Z3)2 = A2A32, (3)

(x - x^2 + (У3 - У1)2 + (z - z^2 = AA2.

В данной системе уравнений xi, yi, zi - координаты точек А1, А2, А3 (соответ­ственно i=1,2,3) в глобальной системе ко­ординат Oxyz.

Преобразование координатной сис­темы O1x1y1z1 в координаты системы Oxyz выполняется по уравнениям:

X0i = a11x1i + a12y1i + a13z1i + xc,

У0І = a21x1i + a22Yu + a23z1i + УС, (4)

Z0i = a31x1i + a32y1i + a33z1i + zc,

X

Где коэффициенты при координатах - на­правляющие косинусы системы O1x1y1z1 относительно системы Oxyz.

Используя матрицы перехода из ло­кальной системы координат O1x1y1z1 в глобальную систему координат Oxyz, по­лучаем координаты векторов rOAk в ви­де функций от неизвестных углов Jk.

X01		R - Lj(t) • cos уj
У01		0
Z01		L1(t) •sin У1

0

2

2

*oa2

L2(t) • Sin Ї2 -(R - L3(t)cos y3) • cos600

V = У03 = -(R - L3 (t) cos У3) •cos 300

L3(t) • sin y3

X02
У02	=
Z02
X03
У03	=
Z03

ROA1

(R - L2(t)cos y2) • cos300

— I

(5)

Рис. 1. Расчетная схема параллельной платформы.

В матричной форме уравнения (4) имеют вид:

R0i

(6)

T10 • r1i;

Где

X0i		X1i		A11	A12	A13	Xc
У0І		У1І	T = ' 40	A21		A23	Yc
	, ?н =
Zi		Z1i		A31		A33	Zc
1		1		0	0	0	1

R>i

Для определения положения плат­формы А1А2А3 используем углы Эйлера в (угол нутации), ф (угол вращения), у(угол прецессии) и координаты центра масс платформы xc, yc, zc.

Vi

V2

(8)

C

C

R = Л

1і 13

Таким образом, получим положение шарниров Л; в неподвижной системе ко­ординат:

A11	A12	A13	Xc		R1		A11 • R1 + xc
A21	A22	A23	Yc		0		A21 • R1 + yc
A31	A32	A33	Zc		0		A31 • R1 + Zc
0	0	0	1			1			1
A11	A12	A13	Xc			R1	• cos 600
A21	A22	A23	Yc		R1	Cos300
A31	A32	A33	Zc			0
0	0	0	1			1

R1	Cos600	+ a22	• R
R1	Cos600	+ a32	• R
		1
A11	A12	A13	Xc
A21	A22	A23	Yc
A31	A32	A33	Zc
0	0	0	1

-a11 • R1 • cos600 + a12 • R1 • cos300 + xc

-R1 • cos 600 - R1 • cos300 0 1

-a11 • R1 • cos60 - a12 • R1 • cos30 + xc

0 - a12 • R1 • cos300 - a21 • R1 • cos600 - a22 • R1 • cos300 + yc - a31 • R1 • cos600 - a32 • R1 • cos300 + zc 1

(7)

Отсюда, получим 9 скалярных уравнений вида:

R-L1 (t)• cosУ1 =an • R1 + Xc

0 = a21 • R1 + yc

L1 (t) • sin У1 =a31 • R1 + Zc

- 2(R - L2(t)cos у 2) =

1 >/3

= - 2an • R1 + 2" a12 • R1 + xc

S

— (R - L2 (t) cos у2) =

1 л/3

1

L2(t) • sin у2 = — a31 • R1 +--- a32 • R1 + z

2

= - 2a21 • R1 + a22 • R1 + yc

V3

C

2

- 2(R - L3 (t) cos У3) =

1 V3

= - 2an • R1 2~ a12 • R1 + xc

V3

- ^(R - L3 (t)cos У3) =

1 s

= - 2a21 • R1 a22 • R1 + yc

1 V3

L3(t) • sin У3 =- ^2a31 • R1 -^"a32 ^ R1 + Zc (9)

Решая систему относительно у;, мож­но получить связь между длинами штанг и углами Эйлера и координатами центра масс системы.