Обычно пористость материала Я определяется как отноше­ние общего объема пустот к объему тела в целом. Пористость равна нулю, когда твердое тело не содержит пор или трещин:

J-J _______________________ объем пустот Vn

Общий объем У

Пли

TOC o "1-3" h z j j-j_____________________ объем твердого тела __________ VT

Общий объем V0

Эффективная пористость ПВ<Ь(Ь

П _______________ Объем эффективных пустот ^ефф

■'■'эфф — ----

Общиіі объем ]/

л

Существует целый ряд методов и установок эксперимен­тального определения пористости различных материалов. В табл. 1 в качестве примера приведены физические свойства шпчных пористых материалов.

Удельная поверхность. Под удельной поверхностью обычно понимаю г площадь внутренних поверхностен пор на единицу ооьема материала. Удельная поверхность определяет пропп - ааемої п, члпп. члирпонорпегот гелп, г е способное*, тел я пропускать через себя жидкость

„ площадь пор,1-м

V л t U - 1-

Объем

В табл. 2. 3 и 4 в качестве примера нрпведеп. ы зависимости і - ^ффпцпеита пронпцаемосіп от ряда параметров пористых материалов

2. Распределение пор по радиусу

Наличие в теле пор различных геометрических размеров. чіп rcf функцией распределения пор по размерам. Если ноль оваться понятием гидравлического приведенного диамет­ра пор, г е. если предполагать, что условные поры имеют вид сфер, объем чоторых равен фактическому, п эти сферы харак - 1 рн мг. гея условными диаметрами, можно ввести фупкшио распределения а(г), определяемую уравнением

Dv —а (г) dr. (1.1)

І і1 dv обьем пор, имеющих радиусы от г до r+dr. Здесь s обьем всех пор, имеющих радиус г или больше г.

Чаще всего пористые материалы и фитили таких аппаратов, і ік іеплопередающие трубки, имеют размер пор от 0,1 до 1000 I (.іпГиі.'їсі - по'ілп'їяіцнм мсіпдом ч. чи < шрсдс. ченпя

(jniiMuin распределения nop u jtom днапашпо является метод ртутлого поромера. По измерению давлення, необходимого для того, чтобы вогнать ртуть гаїутрь пористого тела, п по регистрации объема ртути в порах определяют кривую распре­деления пор по радиусу.

^обк'^НСХ

Таблица 2 Влияние формы частиц на проницаемость

—0,200^—0,160	4,05	3,04	2,50
—0,050	3,18	1,78	1,15

Размер частиц порошка, мм

Отношение коэффициентом при пористости

28%

33.0 %

44.0%

Таблица 3 Зависимость коэффициента проницаемости от природы фильтруемой жидкости (I49J Характеристика пористой ленты Толщина, Коэффициент проницаемости, миллиОарси. определенный Порошок ] Мм А. ютом J Керосином | Дистилли - ропанной подой Медный Нихром Нержанеющая сталь Желечный, фракция —0,45 ; -0,315 /Келечпиіі, фракция —0,315+0,180 Железный, фракция —0.180+0,100 Желе-іньїй, фракция —0,050 0,68 1,53 1,10 0,50 0,50 0,51 0,91 103,0 75,0 84,3 57,0 69,0 12,5 7,05 74,2 83,0 53,5 65,5 11,7 71,5 57.5 64,2 12.6

Таблица 4 Влияние пористости и рачмера частиц на проницаемость пористой ленты Средний диаметр частиц, мк Т =43,8 % Т —32 % Коэффициент проницаемости, нияяидарси Теор. *) | подсч. Эксп. | теор.*' [ подсч. ") | Эксл.

56,0	2210	416	396	1132	63
78,5	4345	494	465	2225	74	85
125,0	11020	585	551	5660	88	—
178,5	21600	656	605	11030	98	104

*> Подсчет коэффициента проппилемостн проподцлгн но формуле Слнхтс- /■• i (iii) ' 1 III) •|чі|ім.'іі' (I X * > I /.• Ь 1/и" f її ■ ,/ | ;|,|.МД)

Когда несмачиваюіцая жидкость, такая, как ртуть, вдавли­вается в поры, она образует мениски, кривизна которых опре­деляется размерами и формой пор и свойствами материала. Если жидкость не смачивает стенки, то необходимо прило­жить внешнее давление, чтобы вогнать ее в поры.

Для определенного размера пор прилагаемое внешнее из­быточное давление определяется уравнением Лапласа—Юнга

Где АР— падение давления на поверхности раздела ж па­кость— пар; о—коэффициент поверхностного натяжения-. Rі и R2 — радиусы кривизны, необходимые для описания трехмер­ной поверхности в пространстве. Если предварительно отка­чать газ из пор фитиля, а затем вдавливать жидкость, то Р=*АР при условии, что парциальное давление паров жидко­сти мало.

Безусловно, реальные размеры пор далеки от сферической г. ли цилиндрической формы, однако часто пользуются эквива­лентным радиусом пор, который определяется как

Где S — площадь поперечного сечения поры; L периметр поры.

TOC o "1-3" h z FaL = PS, (1.3)

Где F„ — сила поверхностного натяжения на единицу длины поверхности раздела.

Fa = a cos Ф, (1.4)

Где Ф — угол контакта жидкость — твердое тело.

Объединяя вышеприведенные уравнения, получаем

Pr = 2о cos Ф. (1.5)

Для постоянных величии поверхностного натяжения и угла смачивания это уравнение непосредственно связывает радиус пор г с давлением Р, необходимым для проталкивания несма - чивающей жидкости в пористую среду.

В дифференциальном виде уравнение (1.5) можно предста­вить как

Nil' | /'с/г 0. (1. (>

Комбинация уравнения (1.1). (1.3) и (1.5) дает выражение для определения функции распределения пор по радиусу

Р2

(1.7)

DV

(2а cos Ф) dP

Для определения а(г) необходимо измерить Р и v. Рассчи­тав а(г), мы по формуле (1.7) можем найти г, зная о и угол Ф. Для ртути о=473 дн/см при 20 °С, а угол Ф~ 130° (для метал­ів

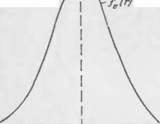
/Т Р'|С- Типичная кривая распреде­

Ления пор по радиусам

Лов). Производную dv/dP можно панти из графика за­висимости Р от v.

На рис 1 приведена ти­пичная кривая распределе­ния пор по радиусу.

І Із уравнения (1.5) нахо­дится диаметр пор

D

(1.8)

4 a cos Ф

Часто вместо гидравлического диаметра пор пользуются шаметром пор в виде медианы D„. Она определяется как ха­рактерный размер поры, когда 50% поры заполнено жндко-

С1ыо.

В табл. 5 приведены данные по измеренным гидравличе­ским диаметрам пор п D„.

Отношение проходного сечения пор пористого материала к общему поперечному сечению. Отношение проходного сечепня і общей площади поперечного сечепня пористого тела опреде­ляется как

При этом предполагается, что тело изотропно п что размеры пор, по которым может двигаться жидкость, существенно мень­ше размеров тела.

Рассмотрим пористое тело в виде бруса длиной ль в на­правлении х и площадью поперечного сечения 5общ в направ - тенин, перпендикулярном X.

FS

П. Ір

Ибис

Lit

Lit уравнения (19) площадь пор находится как

Таблица 5 Гидравлический диаметр пор некоторых материалов

Гидравличес­кий диаметр

Диаметр пор, мк

Материал

П =

(1.10)

Общин объем тела можно представить в виде

(1.11)

Аналогично

(1.12)

Ипар — fj О

Тогда порпстость П можно найти

[ FSoCnndx

(1.13)

/7 = —

Если считать, что поры распределены равномерно по пори­стому телу и их размеры ничтожно малы по сравнению с раз-

Рис. 2. Срез пористом металлокерамики, полученной путем элек­троискрового разряда

Мерами тела, то можно полагать, что отношение проходного еечеиня пор к общему поперечному сечоншо F постоянно, т. е. поверхностная пористость будет равна объемной пористости

F = n. (1.14)

Величина поверхностной пористости может быть полезной при определении потока жидкости через пористый материал, крите­рия Re и эквивалентного диаметра пор

Приготовление срезов пористых материалов. Для опреде­ления поверхностной пористости и размера пор оптическими методами очень важно правильно изготовлять срезы пористых материалов для дальнейшего их исследования с помощью оп тическнх приборов. Традиционные способы распиливания и разрезания пористых материалов часто приводят к искажению истинной картины. Чтобы избежать смятия и деформации пор іасто пористый материал заполняют каким-либо наполнителем (металл, соли и т. д.), который во премя распилнваиня предо­храняет поры, а затем удаляется либо путем нагрева и рас­плавления исполнители, либо каким то химическим способом.

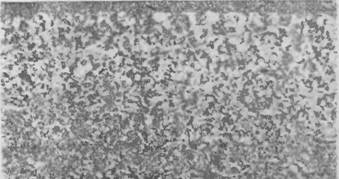
Рис. 3. Срез пористой металлокерамики, полученпой электро химическим способом

Однако при этом является вероятным то, что часть напол­нителя может остаться в порах.

На рис. 2 показан срез материала, полученный с помошыо электроискрового разряда. Диэлектрическая жидкость, прого­няемая по порам тела, одновременно охлаждает образец и уда­ляет стружку.

Этот способ обработки значительно уменьшает деформа­цию пор на срезе.

Одним из перспективных способов разрезания металличе­ских пористых образцов является электрохимический способ (рис.3) Этот способ аналогичен электрогальваническому, только на образец не наносится металл, а, наоборот, снимает­ся слон металла. В данном случае резец и металлическиіі об­разец являются электродами. Электролит (например, раствор соли) прогоняется между резцом и пористым материалом, между которыми приложено электрическое напряжение. Элек­тролит служит электропроводящей и охлаждающей средой, од повременно потоком электролита уносится стружка.