Поперечные колебания стержней
 27 февраля, 2016
27 февраля, 2016  admin
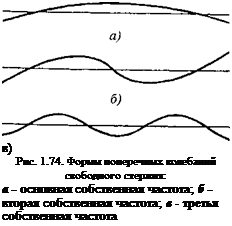
admin Для поперечных (изгибных) свободных колебаний тонких стержней также характерны узлы и пучности смещений и сил. Три первые формы изгибных колебаний тонкого, свободного на концах стержня показаны на рис. 1.74.
Для низшей собственной частоты характерны два узла смещений, для каждой следующей собственной частоты число узлов увеличивается на единицу. Для и-го обертона число узлов смещения и + 1. В отличие от продольных колебаний стержня со свободными концами собственные частоты рассматриваемого стержня не находятся в простых кратных соотношениях, т. е. не являются гармониками.
 Распределение смещений по длине свободноколеблющегося тонкого (d « /.) однородного стержня произвольного сечения [18]
Распределение смещений по длине свободноколеблющегося тонкого (d « /.) однородного стержня произвольного сечения [18]
![]()
![]()
![]()
![]()
chknx + cos кпх-
chknl - coskj sh k„l — sin knl
где kn = ypSml I El - волновое число;
S - площадь сечения стержня; I - момент инерции его сечения.
Значения к„ определяют как корни трансцендентного уравнения
ch к„ I cos к„ I = 1.
Основной частоте стержня соответствует наименьший отличный от нуля корень kl = ai= 4,730. Остальные корни достаточно точно выражаются формулой к„ = (2и + 1 )л/2. Их значения: а2 = 7,853; а3= 10,996; а4= 14,137.
Собственные частоты изгибных колебаний стержня
г _ (К Ї? со (k„lf с0г
" 2 тс/2 S 2 nl2 ’
где г = - радиус инерции сечения.
При и > 1 формула принимает вид
Значения моментов инерции и собственных частот для стержней различных форм приведены в табл. 1.12. Формулы для определения частот справедливы при г/Х < 0,05 или/< 0,01 с,/г.
При изгибных колебаниях свободного на концах стержня крайние узловые плоскости находятся на расстояниях от его концов, равных для первой и последующих мод соответственно 0,22/, 0,13/, 0,096/, 0,07/. Эти точки обычно используют для крепления (опор) образца при испытаниях методом собственных частот в режиме изгибных колебаний. Ввиду меньшей упругости стержней по отношению к изгибу, чем к растяжению-сжатию, низшие собственные частоты изгибных колебаний много ниже соответствующих частот продольных колебаний.
Применение собственных частот продольно - и изгибно-колеблющихся стержней для неразрушающего контроля будет рассмотрено в гл. 4.

 Опубликовано в
Опубликовано в