ПОЛЕ СКОРОСТЕЙ И НАПРЯЖЕНИЙ
 20 ноября, 2013
20 ноября, 2013  admin
admin В качестве реологического уравнения используем ньютоновский закон течения с постоянной вязкостью р.
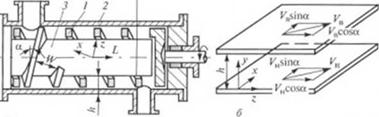
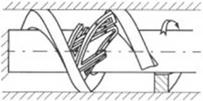
Схема ленточного шнекового смесителя и его плоская модель представлены на рис. 2.74.
Смеситель состоит из пружины прямоугольного сечения / (ленточный шнек), вращающейся с минимальными технологическими зазорами относительно неподвижных корпуса 2 и сердечника 3.
|
|
|
а |
|
Рис. 2.74. Схема неточною шнекового смесителя (а) и его плоская модель (<5) |
Ось z направим вдоль винтового канала, ось х — поперек его, а ось у — но глубине канала. Ширину нарезки обозначим через W, глубину ее — Л, а угол подъема винтовой линии — а. Развернем поверхности ленточного шнека, корпуса и сердечника на плоскости и обратим движение, а течение в канале заменим течением между параллельными плоскостями, как показано на рис. 2.74, б.
Скорость верхней пластины обозначим Уи, а нижней У,„ причем, У„ > У„. По осям z и х действуют положительные по знаку градиенты давления dp/'dz = А. и Ър/Ъх = Ах. Скорость жидкости в направлении осей z и х обозначим, соответственно, v. и vx.
При постановке задачи будем считать, что глубина канала Л меньше его ширины И'и много меньше радиуса ленточного шнека. Утечками через зазоры будем пренебрегать.
Граничные условия для канала ленточного шнека будут:
|
|
|
а решение чисто гидродинамической задачи течения вязкой жидкости в канале ленточною шнека имеет вид |70|: |
|
vxmKix ПРИ >’=°> *хтУшх ПРИ У = и- |
|
*х = Унх+{Уъх-Унх)^ + |
|
|
|
(2.340) |
|
(2.341) |
|
(2.342) |
|
+ - hy)- (2344) |
dv, К,- VH. A,„ fV
i(2y~h); <2-346>
-Л), (2.347)
i n - О,- текущий расхол жидкости; A. (nux) — максимальный градиент давления в н. травлении оси г; vL - истинная скорость жидкости в проекции на ось винта L: I число заходов ленточного шнека.
Существенное влияние на гидродинамику течении вязкой жидкости оказывает безразмерный параметр с = (/„/Сн.
Рассмотрим зависимости (2.341)—(2.347) на конкретном примере ленточного шнекового смесителя, имеющего постоянные геометрические параметры: угол подъема вингговой линии a = 12'; ширина канала W = 0,065 м; число заходов / = I и длина смеси-
гсльной зоны /. = 0,34 м. Вязкость перерабатываемого продукта
составляет р = 320 Па • с.
Исследуем влияние скорости VH и глубины нарезки h на харак - гсристики Q и Az.
|
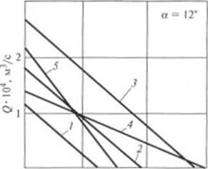
0 I 2 Аг - Iff* 11/м1 0 1.6 3,2 Дд • 10 6. Н/м2 Рис. 2.75. Зависимое!», расхода Q от градиента давления А. (перепада давления др) при различных значениях \ и А. |
|
Значения Р.: / - 0.114 м/с; 2. 4. 5 - 0.182; 3 - 0.265 м/с: in. пении А: 1.2.3- 0.0175 м; 4 - 0.015; 5 - 0.020 м |
Как видно из рис. 2.75, с увеличением скорости К„ (прямые /. 2 и.7) Q и Ар возрастают. Но мерс увеличения глубины винтовой нарезки Л (прямые 4, 2 и.5) расход Q возрастает, а градиент давления I (перепад давления Ар) снижается.
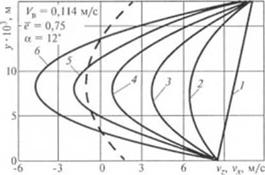
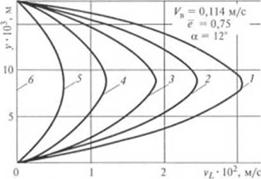
На рис. 2.76 в качестве примера представлено распределение скоростей жидкости v, и vx 110 глубине канала смесителя в зависимости от величины градиента давления Л. при Vu = 0,114 м/с, а = 12* и ё = 0,75. Из рисунка видно, что профиль скорости v. сильно зависит от градиента давления Av а профиль скорости vx (пунктирная кривая), как и следовало ожидать, не изменяется.
|
Рис. 2.76. Распределение по глубине канала ленточною смесителя скоростей г. и е, в мвнснчости от градиента давления А.: |
|
/ — А: = 0; 2— 0.2 Лллк„|; J — 0,4 4 — 0.6 Ллпи„; 3 — 0.8 Л.1пи»); 6 ^гап|
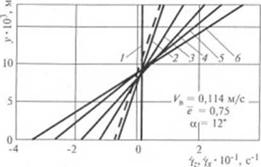
Рис. 2.77. Распределение по глубине канала скоросги жидкости v, в танисичосгм от градисша давления А.: I — А: ~ 0; 2 — 0.2 Дчящу: J — 0.4 ЛЛпм„; 4 — 0.6 Л 5 — 0,8 ЛЛпи1); б — |
Профиль скорости жидкости по оси z (см. кривые 2—6) вызывает предположение о возможности циркуляционного течения вдоль канала винта. Однако такое циркуляционное течение отсутствует, что хорошо видно из профиля скоростей в проекции на ось винта L (рис. 2.77), из которого видно, что при (7 = 0 (Л. = /b, nm)) vi. ~ 0.
|
I'm-. 2.78. Распределение no глхбинс канала простой геометрии скоростей сдвига и у v в зависимости от градиента давлении А.: |
I - А; = 0. 2 - 0.2 Ляша>, 3 - 0.4 Дяжв,: 4 - 0.6 Ллтп,; S - 0.8 Алтп); 6 - АЛят)
При тех же геометрических параметрах ленточного смеситс - |>| рассмотрим распределение скоростей сдвига yz и yv по глубине канала в зависимости от градиента давления А. (рис. 2.78). < корость сдвига в направлении оси х (пунктирная прямая) не гависит от градиента давления Л.. Скорость сдвига в направлении оси z с увеличением градиента давления А. увеличивается и юстигаст своего наибольшего значения при Az= /С(тахц причем координата^, при которой происходит смена знака, не посто - 111на. Следует отметить, что в режиме полностью открытого выхода (Л. = 0, прямая /) скорость сдвига yz *0.
Координаты уа. и у^ можно определить из выражений (2.346) и (2.347), приравняв их к нулю, тогда, соответственно, получим:
|
(2.348) |
|
|
|
(2.349) |
|
Axh |
|
РИС. 2.79. Схема итогового движения •лечен юи жидкое im в канале ленточного шнекового смесителя |
|
V - V ах кх |
|
I- |
|
Уах=ъ |
|
Чу> |
|
IIV |
|
ах, |
|
Как уже отмечалось, для процесса смешения первостепенное значение имеет величина скорости сдвига. Па рис. 2.79 представлена схема итогового движения элементов жидкости в канале лен- Iочного шнекового смесителя. |
|
^ м(*ах "^их). |
|
Уо1~х - |
что свидетельствует о сложности траектории течения, отличной от траектории течения элементов жидкости в канале обычного шнекового смесителя.

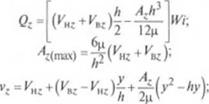
 Опубликовано в
Опубликовано в