Акустическая задержка - протяжен­ная среда со свойствами, отличающимися от ОК, помещаемая между ним и преобра­зователем. Это жидкость в иммерсионном преобразователе, призма из пластика в наклонном или РС-преобразователе (рис. 1.53). Среда задерживает фронт вол­ны на одинаковые (плоскопараллельная задержка) или разные промежутки време­ни. В последнем случае протяженная сре­да является призмой,' обеспечивающей наклонный ввод различных типов воли. Обычно скорость звука в задержке мень­ше, чем в ОК.

Определим некоторые понятия. Аку­стической осью прямого преобразователя называют геометрическую ось пьезопла­стины OaON (см. рис. 1.53, а). Для на­клонного преобразователя так же имену­ется продолжение геометрической оси в призме ОлО в изделие ON после ее пре­ломления на границе призма - ОК (см. рис. 1.53, б). Точка выхода О-точка пере­сечения геометрической оси ОлО с кон­тактной (контактирующей с ОК) поверх­ностью призмы преобразователя. При
малой толщине слоя контактной жидкости она практически совпадает с точкой ввода О, где акустическая ось в изделии ON пе­ресекается с поверхностью ОК (поверхно­стью ввода). Углом наклона акустической оси а называют угол между нею и перпен­дикуляром к поверхности ввода. Угол ме­жду перпендикуляром к контактной по­верхности преобразователя и геометриче­ской осью в призме - это угол призмы р.

Центральный чуч - направление мак­симума излучения. Он может не совпадать с акустической осью, как будет показано в разд. 2.2.4.3. Понятие "угол ввода" также будет определено в разд. 2.2.4.3. Он меньше или равен углу наклона акустиче­ской оси. Основная плоскость - плоскость преломления акустической оси; дополни­тельная (азимутальная) плоскость пер­пендикулярна к основной (перпендику­лярна к плоскости рисунка) и также про­ходит через акустическую ось. Некоторые приведенные определения и понятия не­сколько отличаются от рекомендованных в ГОСТ 23829-85, однако они точнее со­ответствуют физике явления.

Акустическое поле прямого преоб­разователя, т. е. преобразователя с плос­копараллельной задержкой, рассчитыва-

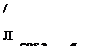
ют, используя понятие "мнимая пьезопла­стина", что показано на рис. 1.53, а штри­ховыми линиями. Расстояние мнимой пла­стины от поверхности ОК равно пхъ, где х3 - толщина акустической задержки; п = с3/с - отношение скоростей звука в задержке и ОК (коэффициент преломле­ния). Продолжения преломленных лучей в направлении задержки приблизительно пересекаются на мнимой пьезопластине (например, для лучей вблизи оси - в точке О'), а изменение фазы волн одинаково для всех точек при переходе от действитель­ной пластины к мнимой, поэтому его можно не учитывать.

Для дискообразного ПЭП с плоско­параллельной задержкой поле излучения вдоль оси

Р « 2P0d| sin[o,25/ra2/(x'+ra:3)]|x хех р[-(8х'+83х3)1

Границу ближней зоны определяют из условия

а2

х'+пх3=а2/Х; х'тах = — - пх3. (1.33 а) К

Здесь РЛ— давление на пьезопластине; х' - расстояние вдоль оси в объекте кон­троля; х'тах - расстояние от преобразова­теля до наиболее удаленного максимума ближней зоны; D - коэффициент прозрач­ности при излучении; к, X - волновое число и длина волны в ОК; 8 и 83 - коэффи­циенты затухания в ОК и задержке.

В практике контроля применяют пре­образователи с длинными акустическими задержками - волноводами, например при иммерсионном контроле - через струю жидкости (струйный контакт), при кон­троле горячего металла - через теплостой­кие стержни. Акустическое поле на торце волновода определяется полем преобразо­вателя и влиянием отражений от боковых поверхностей волновода

Акустическое поле наклонного преобразователя имеет разный вид в ос­
новной и дополнительной плоскостях. В плоскости падения (основной) размер мнимого пьезоэлемента считают умень­шенным в cosa/cosp раз по сравнению с действительным, расстояние вдоль пре­ломленной оси от него до поверхности ввода (т. е. расстояние от центра мнимой пластины О' до точки выхода О) гх = r3ncosa/cos(i, где г3 - средний путь в

задержке-призме ОаО (см. рис. 1.53, б).

Такое построение мнимого пьезоэлемента обеспечивает достаточно точное пред­ставление поля в дальней зоне. В допол­нительной плоскости поле формируется так же, как для случая плоской задержки.

Максимумы и минимумы в ближней зоне определяются интерференцией волн в дополнительной плоскости, где пластина имеет размер 2а2. Положение последнего (наиболее удаленного от преобразователя) максимума определяется приближенной формулой, следующей из (1.33 а);

г< тах=у-гЬ (ТЗЗ б)

где г„ах — путь вдоль акустической оси от точки ввода О до максимума.

В основной плоскости максимумы и минимумы практически не образуются вследствие того, что преломленные лучи от симметричных точек пластины, распо­ложенных выше и ниже акустической оси, дают колебания, не совпадающие в точке В по фазе.

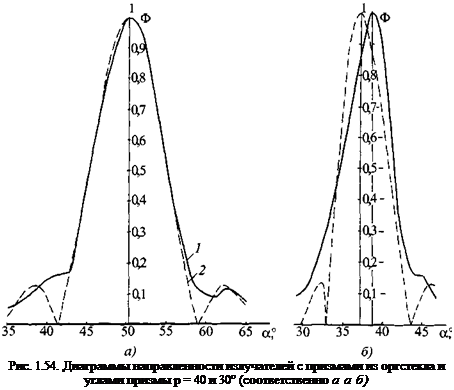
В соответствии с описанным пред­ставлением в дальней зоне наклонного преобразователя (см. рис. 1.53, б) поле излучения в основной плоскости описыва­ется формулой;

Р = РоЛс^ В^)Ф
Xr0'A cos р

с єхр[— (8r' + 5' r3) ]« - C0S - Ф x a r cos a

a------- AsinG,,. exp(-8r'). (1-34)

cosf3

В дополнительной плоскости поле описывается формулой

Р = Р0 ~— £>(р)ф(ай: sin 0г )х

кгОЧ}

х ехр[- (5r'+83r3)]« Рт-f - Ф(ак sin 0 2 )х хехр(-5г'). (1.35)

Здесь г(УВ «г, +г'=г - расстояние между центром мнимого излучателя О' и точкой б; г' - путь ОБ в изделии; Р и а - углы падения и преломления для акусти­ческой оси; 01 - угол падения луча ОлС, соответствующего лучу (76; 0[4] » 0' и 0Z - углы между лучом О'В и акустической осью в основной и дополнительной плос­костях; Рт - 60/j(p)exp(- 5,гэ) - постоян­ный множитель, примерно равный ампли­
туде поля на границе призма-изделие; ф(Х) - функция, характеризующая диа­грамму направленности. Она зависит от формы пьезопластины (круглая, прямо­угольная).

Приближенные части формул (1-34) и (1.35) верны при г'»гх и D(0i)*D(p).

Формула (1.34) справедлива для углов р, отличающихся от критических значений на > 3°.

Построение мнимых пьезопластин в основной и дополнительной плоскостях наклонного преобразователя основано на тех же принципах, что и для преобразова­теля с плоскопараллельной задержкой: продолжения преломленных лучей в на­правлении задержки приблизительно пе­ресекаются на мнимой пьезопластине (на­пример, в точке СУ), а изменение фазы волн одинаково для всех точек при пере­
ходе от действительной пластины к мни­мой.

Пример 1.12. Построить диаграмму на­правленности в плоскости падения в стали для наклонного излучателя с призмой (3 = 40°, диа­метр пьезопластнны 2а = 17,4 мм, частота /= 1,8 МГц, скорости волн: продольной в оргстекле с, = 2,72 мм/мкс, поперечной в стали с = 3,25 мм/мкс (взяты фактические данные из экспери­ментальных исследований)

Находим угол преломления по формуле

(1.13) :

а = arcsin(c sin Р/с2) =

= arcsin(3,25sin40°/2,72)= 50,2°.

С учетом уменьшения размеров мнимой пьезопластины множитель в аргументе функции Ф в формуле (1.34) будет равен

ка' = 2 jt/bcosa/(c cos(3)-

= 2n • 1,8 • 8,7 cos 50,2° /(3,25 cos 40°) = 25,3.

По кривой 2У, {Х)/X (рис. 1.49, штриховая

линия) строим диаграмму направленности излу­чателя. Поскольку множитель £)(Э]) в формуле

(1.34) в данном случае практически не меняется при изменении угла (см. рис. 1.17), воспользуемся приближенной частью этой формулы. Для угла (3 = 40° находим D/f по рис. 1.17, извлекая

квадратный корень из значения П/,', слой жидко­сти отсутствует (5 = 0). Результат построения показан на рис. 1.54, а штриховыми линиями.

На рис. 1.54 показан результат по­строения диаграмм направленности при излучении для ПЭП с призмой из оргстек­ла с Р = 40 и 30°. Параметры преобразова­телей - как в примере 1.12 . Расчетные штриховые кривые довольно близки к экспериментальным, показанным сплош­ным линиями, но отличаются от них, не­смотря на учет при расчетах изменения коэффициента прозрачности в зависимо­сти от угла 9, что не принято во внимание. На рис. 1.54, б хорошо видно отличие угла преломления, вычисленного по формуле

(1.13) , от экспериментального угла для * направления акустической оси, о чем го­ворилось выше (см. рис. 1.27).

Итак, поле наклонного преобразова­теля рассматривают в плоскостях парал­лельной акустической оси и перпендику­лярной к ней - преломленной геометриче­ской оси пьезопластины: плоскости паде­ния и дополнительной плоскости. В плос­кости падения в ближней зоне максимумы и минимумы не образуются. В дальней зоне диаграмма направленности в плоско­сти падения тем шире, чем больше угол наклона.

В дополнительной плоскости в ближней зоне максимумы и минимумы на оси образуются, а следовательно, их мож­но наблюдать на общей оси также в плос­кости падения, хотя неоднородности поля сильно сглажены. Диаграмма направлен­ности в дополнительной плоскости не за­висит от угла наклона.

Согласно EN 12668-2, граница ближней зоны для наклонных преобразователей определяется по расхождению лучей в даль­ней зоне, как было показано для прямоуголь­ной пластины. Рассчитываются разные зна­чения протяженности ближней зоны в плос­кости падения и дополнительной плоско­сти.

Приведем примеры расчетов углов раскрытия для наклонных преобразовате­лей на частоту 2,5 МГц с диаметром пье­зопластины 12 мм (подобных рассмотрен­ному выше прямому) с разными углами ввода. В дополнительной плоскости 9о,1 = 5,6° независимо от угла ввода, по сравнению с прямым преобразователем угол уменьшился, поскольку уменьшились скорость волн и длина волны. Для преоб­разователей с углами ввода 40; 50 и 65° углы раскрытия соответственно 0o, i ~ 6;

6,5 и 10°.

Раздельно-совмещенный преобра­зователь, как правило, имеет призмы, т. е. акустические задержки. Акустическое по­ле PC-преобразователя рассчитывают, построив мнимые пьезопластины для дей­ствительных излучателя 5, и приемника S2.

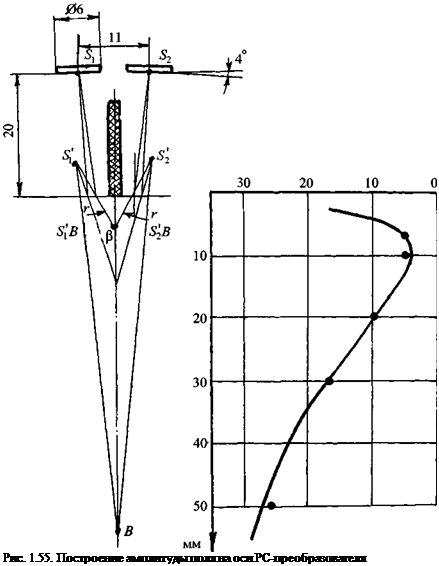Центры мнимых излучателя и прием­ника и S2 (показаны на рис. 1.55). По­ле в точке В находят, вычислив расстояния rS[B > %в вдоль лучей, S'2B и углы

Э', Э" между этими лучами и акустиче­скими осями мнимых пластин, по формуле

ф(а' к sin Є')ф(а" к sin 9")/(r’ г"). (1.36)

Здесь 2а', 2а" - размеры мнимых пьезо­пластин в основной плоскости, постоян­ные множители и коэффициенты прозрач­ности опущены, поскольку они не влияют на изменение поля.

Пример 1.13. Построить поле излучения - приема в стали на оси РС-преобразователя на частоту 2,5 МГц с призмами из оргстекла, разме­ры которого показаны на рис. 1.55. Пластины

имеют прямоугольную форму. Углы призм 4°.

Угол преломления акустических осей для продольных волн

0' = arcsin(5,92 ■ sin4° / 2,72) = 8,7° .

Волновой размер пластин

3-2ti-2,5cos8,7°
5,92 cos 4°

Расстояние мнимых излучателя и приемни­ка от границы призма - ОК

20 ■ 2,72 ■ cos 8,7°/5,92 cos 4° = 9,1 мм.

Поскольку задача симметрична, формула (1.36) приобретет вид

Рв ~ <t>2(7,99sin0)/г'2 .

На рис. 1.55 построены центры мнимых пье­зопластин. Углы и расстояния измерены по чер­тежу. Функцию Ф для прямоугольной пластины находим по рис. 1.49. Результаты построения показаны в виде кривой в сопоставлении с экспе­риментальными точками.

Точку пересечения акустических осей излучателя и приемника называют фокусом PC-преобразователя. Из рис. 1.55 видно, что максимум поля расположен выше фокуса. Это объясняется тем, что лучи, идущие выше фокуса, проходят бо­лее короткий путь и меньше ослабляются.