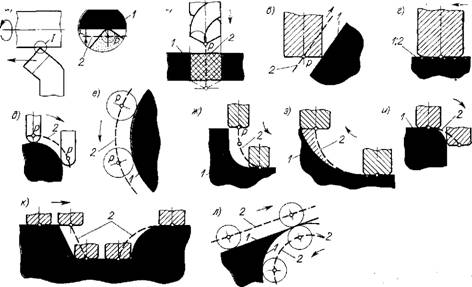
Детали, обрабатываемые на станках с ЧПУ, можно рассматривать как геомет­рические объекты. При обработке детали инструмент и заготовка перемещаются относительно друг друга по определенной траектории. Программа обработки дета­ли задает (описывает) движение опре­деленной точки инструмента — его центра (Р). Для концевой фрезы со сфериче­ским торцом это центр полусферы, для концевой цилиндрической, сверла, зенке­ра, развертки — центр основания, для резцов — центр дуги окружности при вершине и т. д. (рис. 1.15). Если принять, что радиус инструмента во время обра­ботки детали по контуру остается посто­янным, то траектория центра инструмен­та при контурной обработке является эквидистантной контуру детали (рис. 1.15, а — е). Однако это встречается не всегда. Траектория движения центра инструмента может существенно отли­чаться от линий контура детали (рис. 1.15, ж — л), так как в противном случае эквидистантное перемещение инструмен­та или перемещение инструмента точно по контуру привело бы к погрешности об­работки. Поэтому в ряде случаев под эквидистантой понимают такую траек­торию движения центра инструмента, при которой обеспечивается обработка заданного контура.

Движение по эквидистанте относит­ся только к траектории рабочих ходов. Перемещения центра инструмента при обработке детали могут быть также под­готовительными и вспомогательными. Характер этих движений во многом за­висит от задаваемого в начале програм­мирования положения исходной (нуле­вой) точки, от расположения приспо­собления и т. д.

Из сказанного ясно, что для обра­ботки детали по программе прежде все­го необходимо определить рабочие, под­готовительные и вспомогательные траек­тории перемещения центра принятого для работы инструмента.

Относительно контура обрабатывае­мой детали траектория движения центра инструмента при обработке может распо­лагаться по-разному: совпадать с конту­ром, быть эквидистантной контуру, изме­нять положение относительно контура по определенному закону. Для полной обра-

I л) Рис. 1.15. Схемы траекторий центра инструмента: 1 — контур детали; 2 — траектория движения центра инструмента

	Контрольная точка С координатами
QТО	Точка временного останова (30с)

Эквидистанта (траектория рабочего движения)

Смена инструмента )№ позиции (3)

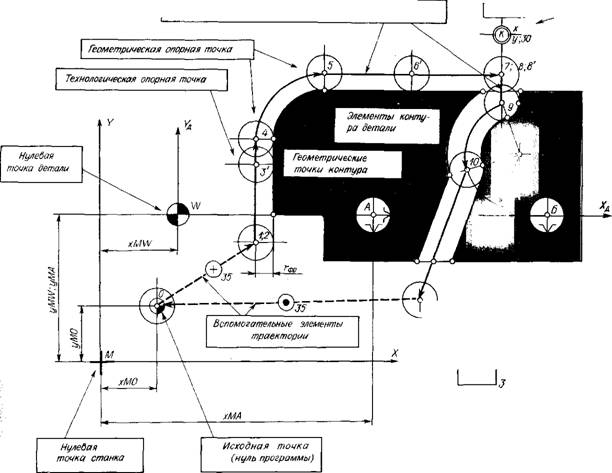
Рис. 1.16. Элементы траектории инструмента при программированной обработке

(•)35 Вертикальный подъем в точке (+) _ Вертикальное опускание 6 точке —(•)— Перемещение с подъемом с —Перемещение с опусканием <

О 1;2 Геометрический элемент (точка 2) в Плоскости, перпендикулярной к рассмат­риваемой

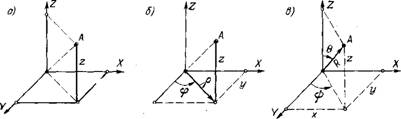
Рис. 1.17. Системы координат: а — прямоугольная; б — цилиндрическая; в — сферическая

'V X У / X

Ботки детали (для выполнения заданной операции) траектория движения центра инструмента должна быть непрерывной. Разработать (определить) ее сразу как единое целое практически очень трудно, поскольку в общем случае программи­руемая траектория является достаточно сложной, определяющей перемещения центра инструмента в пространстве. По­этому в практике программирования траекторию инструмента представляют состоящей из отдельных, последователь­но переходящих друг в друга участков, причем эти участки могут быть или участ­ками контура детали, или участками эквидистанты.

В общем случае участки траектории движения центра инструмента и траек­торию в целом удобно представить гра­фически, исходя из зафиксированного определенным образом положения кон­тура обрабатываемой детали (рис. 1.16).

Отдельные участки контура детали и эквидистанты называются геометриче­скими элементами. К ним относятся отрезки прямых, дуги окружностей, кри­вые второго и высших порядков. Точки пересечения элементов или перехода одного элемента в другой находят как геометрические опорные (узловые) точ­ки. Эти точки в большинстве случаев являются определяющими при задании положения элементов контура (экви­дистанты) в пространстве. Это положе­ние, так же как и величина и направле­ние движения инструмента, задается в системе координат с определенной задан­ной нулевой точкой. Такая точка может быть у станка — нулевая точка станка (нуль станка) или у детали — нулевая точка детали (нуль детали). Она явля­ется началом системы координат дан­ной детали.

Нуль детали W (см. рис. 1.16) может быть задан относительно нуля станка М соответствующими координатами xMW, yMW Свою систему координат имеет инструмент, приспособление. Естествен­но, что при программировании следует учитывать взаимосвязь всех систем коор­динат (см. гл. 2).

В системе координат станка коорди­натами хМО и уМО может быть задана исходная точка О, которая используется для начала работы по программе. Обыч­но с этой точкой перед началом работы совмещают центр инструмента.

В станках с ЧПУ наиболее употреби­тельны прямоугольные (декартовы), ци­линдрические и сферические системы координат (рис. 1.17).

В прямоугольной системе координа­тами некоторой точки А называются взя­тые с определенным знаком расстояния Х, у и г от этой точки до трех взаимно перпендикулярных координатных плос­костей. Точка пересечения координатных плоскостей называется началом коорди­нат, а координаты х, у, Z — соответствен­но абсциссой, ординатой и аппликатой.

В цилиндрической системе координат положение точки в пространстве задает­ся полярными координатами: радиусом р и центральным углом <р (положение про­екции точки на основной плоскости), а также аппликатой 2 — расстоянием от точки до основной плоскости.

В сферической системе координат точка задается длиной радиус-вектора R, долготой и полярным углом 6.

Переход из одной системы координат

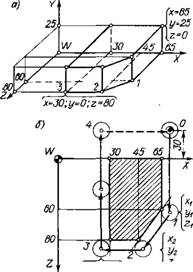
XjW.ZJ Траектория обработки: точки 0-1-2-3-4-0 Рис. 1.18. Схема определения координат опор­ных точек контура детали (а) и траектории движения центра инструмента (б)

В другую осуществляется путем неслож­ного пересчета.

Таким образом, в определенной систе­ме координат контур детали и траекто­рия перемещения центра инструмента от­носительно этого контура могут быть представлены геометрическими элемен­тами с опорными точками, заданными координатами или в пространстве, или на плоскости (рис. 1.18).

На траектории движения центра ин­струмента могут быть назначены также технологические опорные точки, т. е. точки, где изменяются какие-то техно­логические параметры, например подача инструмента и др., точки временного останова с указанием времени останова и т. д. (см. рис. 1.16).

При обработке детали инструмент может перемещаться или в одной плос­кости — плоская обработка, при которой используются две управляемые коорди­наты, или иметь сложное перемещение в пространстве — объемная обработка. Однако чаще всего объемные поверх­ности деталей обрабатывают строчками, каждая из которых является плоской кривой.

Опорные точки на траектории движе­ния инструмента позволяют представить эту траекторию как определенную по­следовательность точек, проходимых центром инструмента (см. рис. 1.16) при обработке детали. Каждое из положений (каждая опорная точка) в выбранной системе координат может быть опреде­лено числами, например координатами. Сочетание таких чисел, определяющих ряд последовательных положений инст­румента, или, иначе, ряд опорных точек траектории, и будет представлять основ­ную часть программы работы станка, выраженную в числовом виде (см. рис. 1.18).

Рис. 1.19. Схема расположения детали на станке: а — деталь в системе координат де­тали; б — размещение детали на станке; В — система координат приспособления

Рис. 1.20. Схемы задания координат опорных точек 1—3: а — абсолютные размеры; б — размеры в приращениях

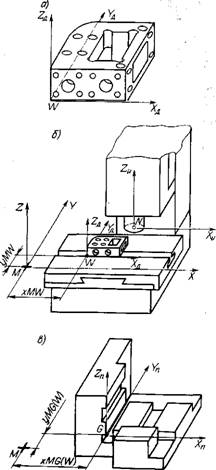
В начале программирования в систе­ме координат детали задают по­ложение базовых элементов заготовки (рис. 1.19, а). Относительно нуля детали (точка W) задаются при программирова­нии все опорные точки, определяющие траекторию движения центра инструмен­та при обработке.

При установке детали на станок (рис. 1.19,6) положение нуля детали (точки W) будет зафиксировано относи­тельно координатной системы станка XYZ Координатами xMW, yMW, zMW.

Если при обработке детали использу­ют приспособление (рис. 1.19, в), то оно должно быть закоординировано на стан­ке относительно нуля станка (точки М).

Система Z„NX„ определяет координат­ную систему инструмента (см. рис. 1.19, б).

Естественно, что при установке дета­ли в приспособлении координатная си­стема детали XAWYA должна совпадать с координатной системой приспособле­ния X„GY„.

При обработке детали при движении по элементам траекторий (прямым, ду­гам, кривым) в промежутках между опорными точками инструмент в опре­деленных случаях может перемещаться по траектории, несколько отличающейся от заданной. Однако можно задать такое число опорных точек, при котором откло­нения фактической траектории от требуе­мой будут меньше некоторой наперед заданной величины и деталь будет обра­ботана в пределах заданной точности.

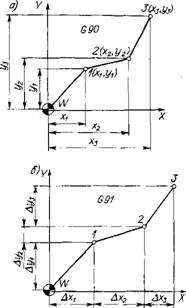
Таким образом, начальный этап пред­ставления траектории обработки детали связан прежде всего с получением коор­динат опорных точек траектории. Эти координаты могут быть выражены абсо­лютными размерами, т. е. для каждой опорной точки заданными относительно нулевой точки станка или детали (рис. 1.20, а), или задаваться в виде прираще­ний в направлении движения инструмен­та от одной опорной точки к другой (рис. 1.20,6). При записи УП способ задания кодируется буквенно-цифровы­ми символами G90 (абсолютные коорди­наты) и G91 (размеры в приращениях). Так, при перемещении центра инструмен­та (рис. 1.20,6) из точки W в точку 1 координата х изменится на величину Axi, а координата у — на величину Дг/i; при дальнейшем движении из точки / в точ­ку 2 приращение по оси X составит А*г, по оси Y — Дг/2 и т. д. Задание координа­тами точек траектории движения центра инструмента зависит во многом от спосо­ба задания размеров детали (рис. 1.21).

В большинстве систем ЧПУ работой станка управляют дискретно, с помощью импульсов. Цена одного импульса (наи­меньшее программируемое перемеще­ние), или дискретность системы, отража­ет разрешающую способность комплекса, включающего систему ЧПУ, механизм подач и датчики обратной связи. Исходя из дискретности системы приращения ко­ординат между опорными точками тра­ектории можно выразить не в мм, а коли­чеством импульсов. Например, если дискретность по оси X составляет 0,01 мм/имп., а по оси Y — 0,02 мм/имп., то значения Ах и ДУ, равные, например, соответственно 12,85 мм и 8,6 мм, в им­пульсах будут выражены следующим образом: Ах =1285 имп., Ду = 430 имп.

Задание приращений по двум осям координат, однако, еще не определит

J

I

<4

70 120 X

20

В

В5< 40 15

& W Yk

L + Y -X I +X

S)

50

70

Г

£

J->

2 o—

W

■■нш

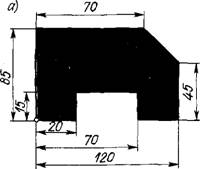
Рис. 1.21. Схемы задания размеров деталей: а — абсолютные размеры (х, у); б — относитель­ные размеры (ЛV, Л;-): Точка У Дх Ау Точка X У Лх А У Мм Мм

W	0	0	0	0
1	20	0	+ 20	0
2	20	15	0	+ 15
3	70	15	+ 50	0
4	70	0	0	-15

5	120	0	+ 50	0
6	120	40	0	+ 45
7	70	85	— 50	+ 40
8	0	85	— 70	0

Заданного прямолинейного движения инструмента между точками. Даже при постоянной скорости подачи по осям вследствие неравенства координат задан­ной точки (AXi^AJ/i) время движения по оси X не будет равно времени движе­ния по оси У и заданная траектория будет искаженной (на рис. 1.22, а пока­зано штрихами). Как уже говорилось, приблизить фактическую траекторию к заданной можно введением дополнитель­ных (промежуточных) опорных точек (точки 2 — 5 на рис. 1.22, б) и заданием соответствующей последовательности пе­ремещений инструменту между этими точками, например: (Ах, А у)-, (2Ах); (2Ах, 2А у); (Ах); (Ах, А у), т. е. траекто­рию по сравнению с ранее определенной (см. рис. 1.22, а) приходится разбивать на более мелкие участки. Величина S оп­ределит ошибку в отработке.

При программировании введение до­полнительных опорных точек приводит к резкому увеличению расчетов и объема программы. Поэтому в практике деталь­ное представление заданной траектории движения инструмента между двумя опорными точками (с выдачей команд на соответствующие перемещения по осям) осуществляется с помощью спе­циального вычислительного устройства — элемента УЧПУ — интерполятора. Ин­терполятор непрерывно, т. е. в каждый данный момент, в процессе перемещения

Рис. 1.22. Линейные траектории перемещения центра инструмента

(в соответствии с заданными прираще­ниями) инструмента от одной опорной точки к другой поддерживает функцио­нальную связь между координатами опорных точек, т. е. обеспечивает отра­ботку траектории в зависимости от вида функции. Если функция выражает пря­мую линию, то отрабатываемая траекто­рия будет линейной, а интерполятор называется линейным. В процессе ра­боты такой интерполятор при исходных заданных приращениях Ах и Ayt (см. рис. 1.22, а) непрерывно должен под­держивать такое соотношение скоростей движения инструмента по осям, при кото­ром инструмент будет перемещаться по заданной линейной траектории.

Обеспечить точно функциональную связь между движениями по осям коор­динат в каждой данной точке траекто­рии очень сложно. В большинстве су­ществующих станков перемещение ин­струмента по заданной траектории осу­ществляется приближенно, путем вклю­чения подачи попеременно то вдоль од­ной, то вдоль другой оси. При этом интер­полятор системы управления непрерывно оценивает отклонения от заданной траек­тории и стремится свести эти отклоне­ния к минимуму. Скачки ступенчатой траектории при формировании заданной незначительны. Они равны или кратны цене одного управляющего импульса, поступающего из интерполятора, или им­пульса, формируемого датчиком обрат­ной связи. Например, прямая наклонная линия может формироваться поперемен­ной подачей на приводы импульсов в такой последовательности: один импульс по оси Y и два импульса по оси X (рис. 1.22, в). Поскольку в современных стан­ках наиболее часто цена импульса прини­мается равной 0,001 мм, то перемещение между двумя соседними опорными точка­ми практически можно рассматривать как плавное. Интерполяция может быть также круговой, с помощью полиномов второй и высших степеней и др.

Работа интерполятора как вычисли­тельной машины основана на решении определенных задач. Известно несколько методов интерполяции, среди которых наиболее распространен метод оценоч­ной функции, основанный на решении алгебраических уравнений [15, 73].

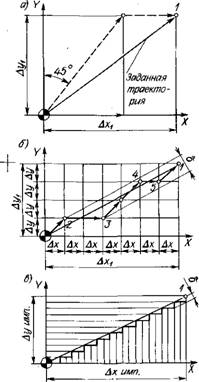
При линейной интерполяции отрезок прямой рассматривается в системе коор­динат, начало которой совмещено с на­чальной точкой То интерполируемого от­резка T0Tk (рис. 1.23, а). Оценочную функцию для любой из промежуточных точек Tj траектории вдоль прямой можно выразить формулой

Fij = yjXk — Xiyk, (1.6)

Где Xk, Ук — координаты конечной точки Tk интерполируемого отрезка; координа­ты начальной точки при интерполяции отрезка прямой равны нулю; х<, г/, — те­кущие координаты точки Г, траектории, определяемые числом элементарных ди­скретных перемещений г вдоль оси X и J вдоль оси У.

Логическая сущность оценочной фун­кции состоит в том, что для всех точек заданной прямой справедливо (рис. 1.23, а) соотношение ук/Xk = yj/xt, или

YkXi = YjXk. ' (1.7)

Разность произведений ytXk — ykXi = = Fij определит зону, где расположена точка. Естественно, что при /•",; = 0 точка находится на прямой, т. е. справедливо соотношение (1.7). Если F, j> 0, то точка находится выше прямой (например, у, больше, чем требуется, или х, меньше); при Fij< 0 точка находится (рис. 1.23, б) ниже прямой (например, г/, меньше, чем требуется, или jc, больше). Таким обра­зом, можно считать, что интерполируе­мая прямая делит плоскость на две части: область f> 0, где оценочная функция после подстановки в нее коор­динат точек этой области принимает положительные значения, и область F<0, где значения оценочной функции отрицательны. Интерполятор определяет последовательность элементарных ди­скретных перемещений в зависимости от квадранта, в котором расположен ин­терполируемый отрезок. Для случая, когда отрезок находится в первом квад­ранте системы координат, направление элементарного дискретного перемещения определяется в зависимости от располо­жения предыдущей точки: если она нахо­дится в области F^O, то дискретное перемещение осуществляется вдоль оси X, если в области F< 0, то вдоль оси У. И так до тех пор, пока текущая точка траектории не совпадет с точкой конца интерполируемого отрезка.

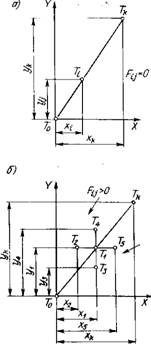
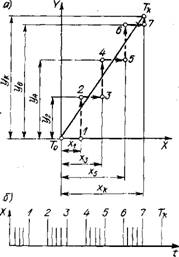
В соответствии с принятым характе­ром перемещений интерполятор выдает попеременно импульсы управления то по одной, то по другой координате. Напри­мер (рис. 1.24, А), если из начальной точ­ки То согласно поданному импульсу управления центр инструмента перемес­тился по траектории Го—1, то интерпо­лятор, определив для координат точки 1 значение функции Fij = yXk — ykX<Q, следующие импульсы будет подавать в цепь управления приводом подач станка по оси Y. После подачи каждого импуль­са интерполятор определяет значение оценочной функции. Как только после по­дачи очередного импульса оценочная функция (Fij = y2Xk — ykXi) изменится, т. е. станет либо равна нулю, либо больше нуля (в точке 2, рис. 1.24, а), интерполя­тор опять начнет выдавать импульсы для управления приводом перемещения

Fij<0

Рис. 1.23. Схемы к определению оценочной функции: Точка Оценочная функция 'Л YiXt — УкХ] = F 11 = 0 Т з УъХь — унх 1 • /'• <0 , 1/4*» — УкХ, =F,„> 0 Г2 УXk — YkX2 = F2l> 0 Т5 УХк — ykXb = Fbt<d

По оси X, прекратив подачу импульсов в привод управления перемещением по оси Y (рис. 1.24,6). В точке 3 значение Fij = угХк — укХз станет меньше нуля и интерполятор обеспечит движение к точ­ке 4, выдавая импульсы в привод пере­мещения по Y. И так далее для всего отрезка от точки То до точки Тк. Следует иметь в виду, что количество импульсов на отрезке перемещения от точки к точке зависит от дискретности системы УЧПУ.

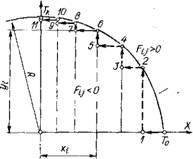
При круговой интерполяции начало системы координат совмещается с цент­ром окружности радиуса R (рис. 1.25, а). Оценочная функция для любой из про­межуточных точек траектории вдоль ок­ружности выражается формулой = = xf--yf — R2. Формула получена из со­отношения xf + yf = R2, справедливого для точек, лежащих на дуге.

А) У Fa'О

1 2 3 4 5 6 7 Тк

1 2 J 4 5 в 7 8 9 Ю 11 12

1 2 J 4 5 В 7 8 9 10 11 12

Рис. 1.24. Линейная интерполяция по методу Рис - 1-25- Круговая интерполяция: а - схема оценочной функции: а — схема траектории; траектории; б — схема подачи импульсов по б — схема подачи импульсов по осям X и Y осям X и Y

Окружность делит плоскость на две части: область F> 0, расположенную вне окружности, и область FС 0, находя­щуюся внутри нее. В зависимости от направления движения вдоль окруж­ности (по или против часовой стрелки) и квадранта расположения интерполи­руемой дуги выбирается правило опре­деления последовательности элементар­ных дискретных перемещений. Для иллю­стрируемого случая проверяется положе­ние текущей точки: если 0, дискрет­ное перемещение осуществляется в от­рицательном направлении оси X, а если F < 0 — в положительном направлении оси Y. Интерполяция начинается в точ­ке Т0 и продолжается до тех пор, пока не будет достигнута точка Тk дуги окруж­ности или граница квадранта. Выполняя работу, интерполятор соответственно на­правляет импульсы в привод подач то по X, то по У (рис. 1.25,6).

СчЕтчик

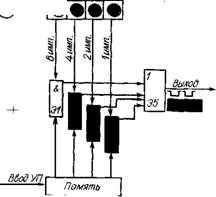
Рис. 1.26. Функциональная схема линейного интерполятора

Ъ T T T I I I I 0 111

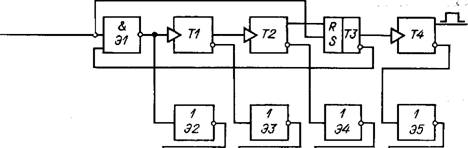
Помимо расчета необходимого коли­чества импульсов для подачи в систему привода той или иной оси интерполятор обеспечивает и выдачу этого количества для управления. Поскольку в УЧПУ большое распространение получили ин­терполяторы, построенные по схеме им­пульсных умножителей, кратко рассмот­рим работу такого интерполятора (рис. 1.26). Задающим элементом УЧПУ явля­ется генератор импульсов (ГИ), который формирует импульсы и подает их с опре­деленной частотой на счетчик интерпо­лятора, Как правило, частота подавае-

ППППП.1

ШинаХ

Л

Гг

& 36

& 37

& 38

<5, 39

Ч T*- 1*2-

Мых импульсов определяется в зависи­мости от программируемой подачи. Для ряда систем ЧПУ частота рассчитывает­ся и записывается в УП. Сделать это нетрудно [6]. Счетчик построен таким образом, что на каждые десять входя­щих в него импульсов (от генератора) с первого его выхода на вход в логи­ческий элемент И (Э1) поступает восемь импульсов; со второго — четыре (Э2); с третьего — два (ЭЗ) и с четвертого — один (Э4), т. е. в системе имеется воз­можность получения импульсов со счет­чика в соответствии с разрядами двоич­ной системы счисления (8421). Вторые входы элементов И (Э1 — Э4) соедине­ны с разрядами регистра памяти интер­полятора, в которой в каждый данный момент находится кодированная (в дво - ично-десятичном коде) информация о за­даваемом перемещении (указано коли­чество импульсов). Следовательно, на вторые входы элементов И с соответ­ствующих разрядов регистра памяти бу­дут поступать нули или единицы, т. е. данные управляющей программы. Так как на вход элементов Э1—Э4 непре­рывно подаются импульсы от генерато­ра в соотношении 8421, то возможность их прохождения через эти элементы к выходному (суммирующему) элементу Э5 определят сигналы на элементы Э1 — Э4 от регистра памяти. Если на элементы Э1—Э4 с регистра памяти поступят единицы, то эти элементы пропустят им­пульсы от счетчика, а если нули — то

	10 имп.		10 имп.	Декада 1
Декада 3	Декада 2

10 имп.

Нет. Итак, на выходе рассмотренного блока линейного интерполятора форми­руется число импульсов, соответствую­щих коду, записанному в регистре па­мяти.

Например, программой задано и введено в регистр памяти число семь; в двоично-деся­тичном коде оно имеет вид 0111 (см. рис. 1.26). Восемь импульсов с первого выхода счетчика не пройдут элемент И (Э1), так как на второй вход Э1 из регистра памяти поступает нуль. Следовательно, с выходов счетчика пройдут на элемент ИЛИ (Э5) соответственно че­тыре, два и один импульс. В результате на выходе блока интерполятора (элемента Э5) Будет сформировано семь импульсов, что соот­ветствует коду в регистре памяти в данный момент.

В целом линейный интерполятор по­строен из нескольких блоков, подобных рассмотренному. Интерполятор может быть выполнен с четырьмя блоками де­кад: тысяч, сотен, десятков и единиц динат (X, У, Z). При этом двоично - десятичный счетчик представляет собой последовательное соединение четырех де­кад; тысяч, сотен, десятков и единиц (рис. 1.28). Импульсы переполнения младших декад служат входными им­пульсами для последующих, старших. Выходы счетчика по одной координате во всех декадах объединены и представ­ляют одну шину отбора (X, У или Z), на которую поступает столько импульсов, сколько закодировано в программе и записано в память по данной координате в данном кадре.

Таким образом, как видно из сказан­ного, объем работ по программированию во многом зависит от системы интерпо­ляции, заложенной в системе управления станком.

Аппроксимация дуг окружностей.

На станках с ЧПУ, снабженных лишь линейными интерполяторами, програм­мирование обработки деталей затрудне­но, если траектории выражены дугами окружностей и кривыми другого порядка. Дуги окружностей для ввода информа­ции в УЧПУ с линейным интерполятором аппроксимируют ломаными линиями с вве­дением по дуге определенного числа опорных точек (рис. 1.29). Величина элементарных участков между точка­ми — участков аппроксимации — зави­сит от углового шага Аф — централь­ного угла дуги, которую заменяют хор­дой, секущей или касательной.

Угловой шаг Аср, а следовательно, и число опорных точек на дуге зависят при заданном радиусе R от принимаемого значения стрелки прогиба б, определяю­щей точность аппроксимации, т. е. сте­пень приближения ломаной линии к дуге окружности. Естественно, что чем меньше
значение принятого углового шага, тем ближе обработанный контур будет по форме приближаться к круговому (за­данному). Но при программировании следует учитывать также, что уменьше­ние б приводит к увеличению расчетных работ и объема программы из-за увели­чения числа опорных точек.

Угловой шаг для заданного радиуса и назначенной величины 5 можно опре­делить или расчетом, или по таблицам, или ориентировочно по графикам. При выборе углового шага следует учитывать характер траектории инструмента. Для облегчения расчетов при аппроксимиро­вании следует использовать специальные таблицы [48].

В современных условиях большинство станков с ЧПУ оснащены УЧПУ с линей - но-круговыми интерполяторами, поэтому заниматься вопросами аппроксимации дуг окружностей технологу-программи - сту приходится сравнительно редко. Эти задачи встречаются в настоящее время лишь при расчетах по аппроксимации кривых второго порядка [28].

При программировании обработки кроме определения величины перемеще­ния центра инструмента по траектории необходимо указать скорости перемеще­ния инструмента между отдельными

Опорными точками, целый ряд вспомо­гательных технологических команд и др. Все это оформляется в виде расчетно- технологической карты (РТК) на обра­ботку данной детали и карты кодирова­ния программы.

В общем случае для составления УП необходимо иметь операционный эскиз детали, чертеж заготовки и РТК, допол­ненную таблицей координат опорных то­чек или расстояний между точками (при­ращений).