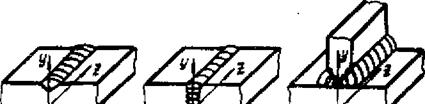Если сварочный нагрев по толщине изделия неравномерен или ширина зоны пластических деформаций значительно меньше толщины изделия, компонента напряжения по толщине может быть существенной, т. е. возникает объемное напряженное состояние. Решение такой задачи в точной постановке в настоящее время связано с очень большими трудностями из-за недостаточного объема оперативной памяти и быстродействия вычислительных машин. Поэтому при построении расчетных схем используют ги­потезу плоской деформации, что позволяет свести объемную за­дачу к плоской.

С целью единой фор­мы записи основных

уравнений для случаев _______________ ________

плоского напряженно - ~о“ ® ' о г*

го состояния и плоской рис.7.12. Примеры сварных соедн - деформации в этом пара- нений, напряженное состояние ко-

графе примем систему координат, показанную на рис.7.12.

Пусть размер тела, свойства материала и нагрузка (тем­пература и внешняя нагрузка) не меняются по длине, а конце­вые сечения ограничены фиксированными абсолютно жесткими плоскостями, которые препятствуют перемещениям в направле­нии оси г. Тогда все поперечные сечения находятся в одних и тех же условиях и три компоненты деформации равны нулю:

і <Ухк. ® ■* /уа. ® і (7*64)

а остальные три компоненты (tx, ty, ) являются функция­

ми х и у и не зависят от г . Рассматриваемая деформация, называется плоской.

При сварке требование постоянства нагрузки по длине те­ла удовлетворяется, если температурное поле (точнее темпера­турная деформация еТ ) по длине не меняется. А это значит, что сварной шов должен выполняться одновременно по всей дли­не (огй— о** ), Практически влияние скорости сварки суще­ственно сказывается на поле напряжений и деформаций только впереди и вблизи источника теплоты, а позади источника, где ■£

Э«,а Эха 0уа

распределение ьт(х) оказывает небольшое влияние на напря­женное состояние. Это значит, что, чем больше тгс (чем мень-

Q1T

we ) и чем больше температурный интервал и меньше вели­чина деформации фазовых превращений, тем меньше погрешность расчетной схемы, основанной на гипотезе плоской деформации.

Если торцевые сечения в процессе сварки не закреплены, заданы перемещения или силовые условия на них, то можно ис­пользовать гипотезу плоских сечений и полные продольные де­формации в приращениях представить в виде

Де, і(х, у')=й£гЛ-ДСуХ-йСху , - (7.65)

где - приращение продольной деформации волокна, сов­

падающей с продольной осью к, і йСх , Aty - приращения кри­визны продольной оси при изгибе относительно осей X и у соответственно. Величины Atz0 , Atx и АСу могут быть за­даны (если заданы перемещения на торцевой поверхности) или определены из условий равновесия сил в поперечном сечении

^ba(x, v)xclxdy=My >t

где "P^ - внешняя продольная сила; МХ1Му - внешние изги­бающие моменты относительно осей х и у соответственно.

Найдем уравнение связи приращения деформации с напряже­нием в форме (7.2?) для случая плоской деформации. Дополни­тельное уравнение (7.65) позволяет формально исключить про­дольную компоненту напряжения ба из уравнения связи и сформулировать плоскую задачу термопластичности. Для этого из третьего уравнения (7.27) выразим

(7.67)

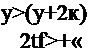и подставим в остальные уравнения, в результате чего получим уравнения связи

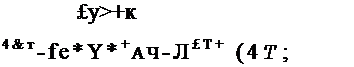Max

В матричной форме уравнения связи имеют вид

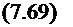И=ЙҐІ.9р1ї°} ,

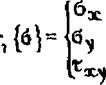где

При упругом деформировании тела (ip = V?- & ) и условии t^s 0 последнее уравнение переходит в уравнение теории тер - ноупругостн, связывающее напряжение и деформацию за весь пе­риод нагружения:

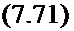1^=И (иНб°Г) *

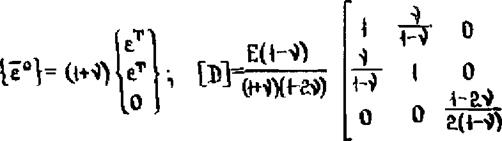где

Величина ftt* в уравнениях (7.67)-(7.70) определена, так как уравнение плоскости fie. t(x,>rt может быть найдено последовательной подстановкой уравнений (7.67) и (7.65) в систему трех уравнений (7.66) и решением ее относительно не­известных, &СХ и .

Сравнивая плоское напряженное состояние и плоскую де» формацию, можно отметить, что структура формул (7*69), (7.70) и (7.60), (7.61) одинакова. Отличие заключается только в

элементах матриц [Б] и [В] ? и дополнительных; деформациях {&°} и {ї0} . Б случае плоской деформации перед вычислени­ем следует решать дополнительную систему (7.66), а в

условие текучести (7Л2) при вычислении интенсивности напря­жений 6$, учитывать компоненту б*. .

Перечисленные отличия не затрагивают основы алгоритма, поэтому методы, решения плоских задач, основанные на гипоте­зах плоского напряженного состояния и плоской деформации, одинаковы.