ПЕРВЫЙ ‘ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ ПОТОКА (ОТКРЫТАЯ СИСТЕМА)
 20 марта, 2013
20 марта, 2013  admin
admin Движущееся по какому-либо каналу рабочее тело образует поток. Этот поток может быть дискретным и сплошным. Термодинамику потоков ограничим следующими условиями:
1) переменные по поперечному сечению потока термодинамические параметры и скорость заменяются усредненными величинами, сохраняющими свое постоянное значение по всему этому сечению потока;
2) рассматриваются только стационарные потоки, т. е. такие, в которых независимо от времени в любом сечении его термодинамические параметры и скорость потока остаются постоянными;
3) рассматриваются только сплошные потоки, т. е. такие, когда через любое поперечное сечение / канала проходит в единицу времени одно и то же количество вещества, т. е.
Ci/i c2j2 cf Mc = = =.,.== — = const, (1.135)
V2 v
Где mc — массовый расход вещества, проходящего через данное сечение канала, кг/с; с — скорость потока, м/с; v — удельный объем вещества, м3/кг; / — поперечное сечение канала, по которому движется поток, м2.
Уравнение (1.135) называется уравнением сплошности; оно характеризует установившееся движение вещества в канале. Представим уравнение (1.135) в виде
Nw==fc (1.136)
И продифференцируем его при т — const, получим
Mdv=fdc + cdf. (1.137)
Поделив уравнение (1.137) на (1.136), получим
Du dc dF df di' dc-------------------- „ ,„,,4 --- _ 1_ J или J - (1.138)
V с j j V c
Как следует из этого уравнения, для того чтобы течение рабочего тела гю каналу было сплошным, должны быть следующие профили канала:
А) если dc/c < dv/v, то d///>0, т. е. профиль канала должен быть расширяющимся;
Б) если 6.с/С > dV/v, то df/f < 0, т. е. канал должен быть суживающимся;
В) если dС/с — dv/v, то df/f = 0, т. е. канал должен иметь постоянное поперечное сечение.
Математическое выражение первого закона термодинамики для потока. В уравнении (1.22) L* представляет собой работу потока, которая состоит из работы проталкивания, технической работы и работы трения.
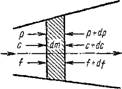
Рассмотрим перемещение в канале элементарной массы рабочего тела dm из сечения 1-1 в сечение 2-2 (dm изображено на рис. 1.22 графически заштрихованной площадкой) за время dx. На левой грани внешнее давление р совершает работу перемещения элементарной массы; на правой грани внешнее давление р + dp, как направленное навстречу движению тела, носит характер сопротивления, преодолевая которое тело совершает работу; поэтому первую работу следует рассматривать как отрицательную (по отношению к телу), а вторую — как положительную. Алгебраическая сумма этих двух работ называется работой проталкивания и для т кг рабочего тела обозначается L (Дж); удельная работа проталкивания обозначается Г (Дж/кг).
Таким образом, за время dx рабочее тело массой dm совершило работу
DL dx = [(р + dp) (/ + df) (с + dС) - р/с] dx.
Пренебрегая бесконечно малыми величинами второго и высшего порядка малости, после сокращения получим
6£ = p/dc + рс df + cf dp = pd (fc) + (fc) dp = d [p (/c)] = d (pV) (1.139) и для 1 кг
51' = d (pv). ' (1.140)
В интегральном виде
V = Сч d ^= № " PlVl' (U41)
Работа проталкивания — это первая часть работы, которую совершает поток. Однако на пути между сечениями канала 1-1 и 2-2 он может совершать и другие виды работы, например вращать колесо турбины, перемещать твердые частицы и т. д. Все эти виды работы потока против внешнего объекта называются технической работой. Обозначим ее L^x. Когда поток движется по каналу, то он совершает также работу по преодолению сил трения на границе со стенкой канала — LrP. Таким образом, работа, которую совершает движущийся по каналу поток вещества, будет
L* = {p2V2 - PiVi) + Lrex + LTP. (1.142)
|
Рис. 1.22. К определению работы проталкивания |
Совмещая между собой уравнения (1.22), (1.23) и (1.142), получим математическое выражение первого закона термодинамики для потока:
Q = W FL_.Il(Я2 - ЯО + АС/ + (p2F2 - PlVx) + Lrcx + Lrp. (1.143)
Поделив уравнение (1.143) на т кг вещества, получим выражение первого закона термодинамики для 1 кг вещества: 2 2
Q = + д (#2 - #0 + Аи + (P2v2 - piVi) + /тех + /тр, (1.144)
Или в дифференциальном виде:
= D (с2/2) + d (дН) + ди + d (Pv) + 8/тсх + 8/тр. (1.145)
Основное уравнение потока и располагаемая работа. Рассмотрим движение по каналу потока, не совершающего техническую работу /гсх = 0. Тогда, пренебрегая изменением потенциальной энергии потока и трением его о стенки канала, уравнение (1.145) примет вид
Bq = d (с2/2) 4- dИ + d (pv) = d (c2/2) + d (u + pv). (1.146)
Так как и + pv = h — есть энтальпия, то окончательно получим
8Q = d (с2/2) + dh. (1.147)
Уравнение (1.147) называется основным уравнением потока. При адиабатном течении потока по каналу без трения уравнение (1.147) принимает вид
Dh = - d(c2/2), (1.148)
Т. е. изменение энтальпии представляет собой изменение кинетической энергии потока при адиабатном течении его по каналу.
Математическая интерпретация закона сохранения энергии применительно к гидродинамическим процессам дана Д. Бернулли в виде уравнения
Dp/p + d (с2/2) = 0, (1.149)
Или
И dp + d (с2/2) — 0. (1.150)
Таким образом, закон сохранения энергии может быть математически записан либо уравнением (1.147), либо уравнением (1.150). Тогда, совмещая эти уравнения между собой, получим, что
8Q — dh — vdp = dh — [D(Pu) — Pdv] = D (h — pv) + p dv — du + P dv,
Т. е. получим уравнение (1.37) первого закона термодинамики для рабочего тела, когда оно находится в относительном покое, т. е. для закрытой термодинамической системы.
Таким образом, для потока, движущегося по каналу без трения, с учетом уравнения (1.146) можно написать, что
8Q = d (с2/2) + du + d (pv) = D (с2/2) + Du + Б/', (1.151)
А с другой стороны, для него справедливо уравнение (1.37). Сравнивая эти два уравнения между собой, видим, что
8/ = D (c2/2) + 5/', (1.152)
Т. е. работа расширения-сжатия потока трансформируется в кинетическую энергию потока и частично расходуется на движение потока — работу проталкивания. Итак, не вся работа расширения-сжатия, а только часть ее, равная (8/ — §/'), превращается в кинетическую энергию потока. Разность работ расширения-сжатия и проталкивания, равная кинетической энергии потока, называется располагаемой работой и обозначается /0.
Таким образом, можно написать, что
8/0 = D (с2/2) = Ы — Ы' = pdv — d (pv) = —vdp, (1.153)
Или в интегральном виде
Л _ „2 Г Pi ГР2''2 fPl
1о= 2 1 - l — l'= pdu- cl (pv) = - J udp. (1.154)
14 Ріі'і ^ Pi
Для жидкостей, паров и реальных газов располагаемую работу можно рассчитать следующим образом: из уравнения (1.147) следует, что d (с2/2) = 8q — dh и, следовательно,
Bl0 = d(c2/2) = bq-dh, (1.155)
Или
/0 = (d - c)j2 = q - Ah. (1.156)
|
/ _ С2 ~ СЇ 10 — п |
Для идеальных газов
2 ,2 ГР2 !
Vdp = / - /' = _ T (px^i - p2v2)
Pi
N
{P2V2 - P1V1) = _ 1 {PiVi - P2V2) = nl. (1.157)
В частности, для адиабатного процесса п = к и для него
К - 1
|
(1.158) |
Iq — kl — _ 1 pivi
■ Покажем, что в координатах р, v площадь, ограниченная кривой процесса, начальной и конечной абсциссами и осью ординат, представляет собой располагаемую работу, т. е. в соответствии с рис. 1.23 пл. а12Ь = /0. Как видно из этого рисунка, площадь заштрихованной элементарной площадки v dp = d/0, и, следовательно, вся площадь а12Ь = /0.
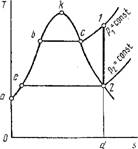
В соответствии с уравнением (1.156) можно написать, что l0 = q + (hx — — h2) = q 4- q°xn, т. е. располагаемая работа в каком-либо процессе равна сумме теплоты этого процесса и теплоты изобарного охлаждения рабочего тела в том же интервале температур (рис. 1.24). Для адиабатного процесса А — С: /0 = - Ah = = пл. AC ab clA.
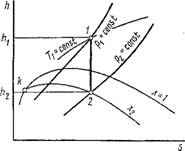
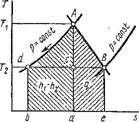
Для адиабатного процесса, протекающего в парах, в системе координат Т, s (рис. 1.25) располагаемая работа изобразится площадью /0 = = hi — /і2 = пл. OabcldO — пл. Oae2dO = пл. edcl2e. Как видно из рис. 1.26,
|
Рис. 1.26. Графическое изображение располагаемой работы паров в координатах H, S |
Эта же располагаемая работа в системе координат /г, S изобразится длиной отрезка 1-2, так как hi — h2 = І о-
Истечение газов и паров. Большой научно-технический интерес представляет процесс истечения упругого рабочего тела из коротких каналов, называемых насадками или соплами. Обычно течение рабочего тела в соплах, связанное с изменением его параметров, происходит настолько быстро, что теплообмен между этим телом и стенками сопла практически отсутствует. Это обстоятельство дает основание считать процесс истечения рабочего тела из насадок (сопл) адиабатным. Кроме того, в насадках отсутствует техническая работа.
Рассмотрим случай адиабатного истечения рабочего тела через сопло из резервуара, где оно находилось под давлением ри имея удельный объем і'ь в среду с давлением рср < Рі (рис. 1.27). Предполагаем, что объем резервуара настолько большой, что истечение веществ через сопло в течение рассматриваемого промежутка времени практически не приводит к уменьшению давления в резервуаре. Из уравнения (1.154) следует, что скорость истечения из сопла
|
Рис. 1.25. Графическое изображение располагаемой работы паров в координатах Т, S |
|
Рис. 1.24. Графическое изображение располагаемой работы в координатах Т, S |
|
Tf 1 |
|||
|
V |
|||
|
B |
Г |
N |
? |
|
Рис. 1.23. Графическое изображение располагаемой работы в координатах р, V |
С2^]/21ОТЯ (1.159)
Обычно Сі по сравнению с с2 ничтожно мала и ею можно пренебречь. В этом случае, опуская индекс у скорости тела на выходе из сопла, можно написать, что
С ='|/2/о. . (1.160)
Для любого рабочего тела в соответствии с формулой (1.156) располагаемая работа /0 = q + (ht — h2) и, в частности, для адиабатного течения L0 — hi — h2. С учетом этого уравнение (1.160) при адиабатном течении примет вид
С - 1/2 (1ц - h2) = 1,4141/їі^іь, (1.161)
Где h — в Дж/ісг и с — в м/с.
Так как в области невысоких давлений с изменением последнего жидкость практически не изменяет свой объем, то в соответствии с уравнением (1.154)
1о = ~ Ур[ Vdp = v{pi~ р2),
И, следовательно, скорость истечения из сопла капельной жидкости
С = ]/2Го = |/Ъ(Р1-Р2) = 1,414 /v(Pl-p2). (1.162)
|
[P1v1 |
|
|
I ^ |
|
|
4 ^рС<Р1 |
|
Рис. 1.27. Истечение рабочего тела из сопла |
Для идеального газа при адиабатном течении в соответствии с уравнениями (1.160) и (1.158) скорость истечения
|
К - I К |
|
2 к |
|
I - |
|
С — |
|
7~Р 1V2 |
|
К - 1 |
(1.163)
Зная скорость истечения, нетрудно определить по уравнению (1.135) массовый расход рабочего тела через сопло.
Проведем анализ истечения из сопла идеального газа. Для идеального газа расход через сопло
K + 1
|
2k |
|
P 2 V Pi |
|
P 2 |
|
■Ї2 |
|
(1.164) |
|
К — 1 vi |
|
Vl |
Cih C2f2
Т0 =
V2
Из этого следует, что mc = 0 при р2 = Pi и при р2 = 0. Чтобы найти максимум Штах, т. е. максимум функции (р2/рі), надо взять производную выражения в квадратных скобках и приравнять нулю. Обозначив переменную (р2/рі) через Р, произведем действие:
К + 1
|
Р* |
|
= 0; 2 |
|
Dp К+ 1 Р к |
|
2 — к Р к |
|
Apt"1 /с 1 |
|
/с + 1 |
|
К + 1 |
|
= 0, или |
|
К К - 1 |
Fc -1 Р к, ИЛИ р
К + 1 г ' *" R к + 1 Таким образом, расход газа через с. опло становится максимальным
К
|
При отношении Pi/Pi = Р |
|
К + 1 |
К -Ї
, которое впредь будем назы
Вать критическим отношением давлений и обозначать ркр. Аналогично этому давление в устье сопла (на выходе из него) р'2, удельный объем V2 и скорость истечения с, соответствующие максимальному расходу газа через сопло, назовем критическими и обозначим через /)кр, VKp и скр. Следовательно, можно написать, что
|
1 к |
|
2 к |
|
2к |
|
1 |
|
Р lOj. |
|
К - 1 |
|
К+ 1 |
|
К + 1 |
Итак, при изменении давления среды от рІ до р2 — р*Р расход идеального газа через сопло увеличивается от нуля до максимума. При дальнейшем понижении давления среды от р2 = ркр до р2 — 0 согласно уравнению (1.164) расход газа через сопло должен уменьшаться от максимума до нуля. Опыты с истечением упругих тел через суживающиеся и цилиндрические насадки показывают, что при дальнейшем понижении давления среды от ркр до нуля расход газа через насадку становится постоянным, равным максимальному, т. е. действительный процесс изменения тс от P2/Pi = 1 до р2/р = О идет по линии Abc (рис. 1.28). Это расхождение теории с действительностью объясняется тем, что в устье цилиндрического или суживающегося сопла при давлении среды Рср < РкР устанавливается свое давление р'2 = ркр независимо от давления среды. Этому постоянному давлению потока на выходе из сопла, естественно, будет отвечать постоянный расход рабочего тела через сопло, равный максимальному значению wmax.
Покажем, что критическая скорость потока в данном сечении канала равна местной скорости звука в нем. В самом деле,
Понижение температуры в потоке при критической скорости согласно уравнению (1.165) равно
Fc - 1
|
'кр ТГ |
Гк„ / рКр '' 2 Pi
_ _ /с - f - 1
11 — « І кр>
Что при подстановке в уравнение (1.167) дает известное из курса физики выражение местной скорости звука
А = }/кВХр = /кр^7Р. (1.168)
Так как R = 8314/ц, то а = ]/8314/с71-рДі. Отсюда следует, что местная скорость звука, а следовательно и скр, уменьшается с увеличением молярной массы газа и с уменьшением к и Т.
Теперь можно сказать, что критическими параметрами рабочего тела при течении его в канале называются термодинамические параметры в том сечении его, где скорость потока равна местной скорости звука.
Итак, нами установлено, что при истечении рабочего тела из цилиндрического или суживающегося сопла скорость потока на выходе из него не может быть больше местной скорости звука. А это значит, что при истечении упругих тел, в частности идеального газа через цилиндрические и суживающиеся сопла в среду с давлением рср < ркр, только часть потенциальной энергии потока, соответствующая перепаду давления от рі до ркр, переходит в кинетическую энергию потока, хотя поток по выходе из сопла и будет продолжать расширяться с понижением своего давления от Ркр до рср, но это расширение будет происходить неорганизованно и потенциальная энергия потока будет расходоваться на образование вихрей и т. д.
Поставим перед собой задачу построить такой профиль сопла, который обеспечил бы полное превращение потенциальной энергии потока, соответствующей перепаду давления от ру до р2 = рср, в кинетическую энергию потока по выходе его из сопла. Для этой цели проведем анализ уравнения (1.138): df/f = dv/v — dc/c.
Так как — v dp = d (с[1]/2) = с dС, то, поделив это уравнение на с2, получим
-Vdp/c2 = dc/c. (1.169)
Продифференцируем уравнение адиабаты pvk = const, получим Kpvk~ldv + vkdp = 0. Поделим это уравнение на pvkk, тогда
TOC o "1-3" h z df dp Л dy dp „
---- + -І— = 0, или — = - (1.170
V kp v кр
Совмещая между собой уравнения (1.138), (1.169) и (1.170), получим Df dp t vdp kpv — с2 , a2 - с2 , ..
Проанализируем уравнение (1.171). Так как крс2 > 0, a dp < 0, то во всем диапазоне изменений скорости истечения с от 0 до с < а в соответствии с уравнением (1.171) df/f < 0, т. е. профиль сопла должен быть суживающимся. При c = a = cKp d///=0 и/ = /min, т. е. в минималь-
Рис. 1.28. Зависимость массового расхода газа через сопло от отношения р2/рІ
Рис. 1.29. Зависимость профиля сопла Лаваля от скорости в нем потока и перепада давления
Ном сечении сопла будем иметь критические параметры скр, vKp, ркр и Гкр. Из уравнения (1.171) следует, что при всех скоростях истечения выше скорости звука (с > а) профиль сопла должен быть расширяющимся, так как в этом случае d///> 0. Впервые профиль такого сопла был предложен шведским инженером Л авалем. Очевидно, сопло Лаваля позволяет получить скорость потока рабочего тела, выходящего из насадки, выше скорости звука в данной среде. На рис. 1.29 приведен профиль сопла Лаваля и характер изменения в нем р и с при течении в нем рабочего тела.
В инженерных расчетах химической технологии для реальных газов и перегретых паров низких давлений ркр, а следовательно, и ркр находят из уравнения (1.165). Так, для перегретого водяного пара, приняв как для трехатомного газа к = 1,3, из этого уравнения находим ркр = 0,55.
|
(1.172) |
Скорость пара или реального газа на выходе из сопла рассчитывается по формуле (1.161), а критическая скорость истечения — по формуле
Скр = 1,414]//!! - k
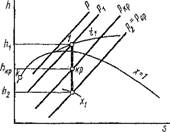
В этих формулах Hi, H2 и HKp находятся либо по /is-диаграмме, как это указано на рис. 1.30, либо с помощью таблиц: Hi — по Pl и гь H2 — по
Р2 И S2 = SІ И /ікр - ПО рКр И SKp =
Для расчета секундного расхода пара или реального газа через сопло, либо для расчета его характерных сечений /min и /тах используется уравнение сплошности (1.135). Входящее в это уравнение v2 или укр находится или непосредственно из /«-диаграммы, как это наглядно показано на рис. 1.30, или с помощью таблиц: v2 — для р2 и s2 =
= Si И Гкр - ДЛЯ р,ф и SKp = Si.
|
(1.173) |
Температура торможения. При адиабатном течении рабочего тела в неподвижном канале уравнение (1.147) принимает вид
D (с2/ 2) + Dh = 0.
Таким образом, всякое изменение кинетической энергии рабочего
|
|
Рис. 1.30. Графическое изображе - Рис. 1.31. Изображение процесса тормо-
Ние процесса течения рабочего жения потока
Тела по соплу Лаваля в координатах H, S
Тела будет вызывать соответствующее (обратное) изменение его энтальпии, а следовательно, и температуры.
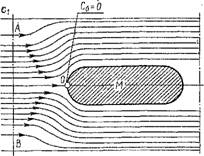
Пусть поток при адиабатном течении набегает на какое-либо тело М. Тогда в соответствии с рис. 1.31 какая-то центральная струйка рабочего тела (потока) при ударе по нормали о тело М в точке О, полностью потеряв свою кинетическую энергию, повысит свою температуру. Точка, в которой скорость рабочего тела обращается в нуль, называется Точкой нулевой скорости, а температура в этой точке — температурой полного торможения. Для определения этой температуры напишем интегральное выражение уравнения (1.173) для газа:
Срт (Т2 - 7"i) + (El - Cj)/2 = 0. (1.174)
Пусть Ті и Сі относятся к некоторому сечению А-В газового потока, в котором газ еще не испытывает влияния на свое движение тела М, а Т2 и С2 — к газовому потоку в точке О. В этом случае с2 = 0, а температура торможения Тт = Т2 найдется из уравнения (1.174):
Т? = Ті + с1(2срп). (1.175)
Для идеального газа ср = с„ + R = Cp/K + R, или
Ср — —-— R.
Р к - 1
Подставляя это выражение в уравнение (1,175), получим
К - 1 1с?
П +
R 2
Для воздуха газовая постоянная R = 287 Дж/(кг-К); к = 1,4 и поэтому для него уравнение (1.175) примет следующий вид:
Тг = Ъ + 5 (cj/100)2.
|
|
Диффузор. При течении рабочего тела в соплах (насадках) имеет место непрерывное понижение давления и возрастание скорости потока, т. е. в соплах протекает процесс превращения потенциальной энергии в кинетическую. Каналы, в которых происходит превращение
кинетической энергии потока в потенциальную, т. е. повышение давления за-счет снижения скорости потока, называются диффузорами. Так как в диффузорах всегда Dp > 0, то из' формулы (1.171) следует, что при всех значениях скорости потока при входе в диффузор Ci < а = скр профиль его должен быть расширяющимся (d / > 0), а при с І > а = скр он должен быть сперва суживающимся (d/< 0), а затем расширяющимся (d/> 0). В первом случае давление потока возрастает до р2 ^ ркр, во втором — в минимальном сечении диффузора он достигает величины ркр, А затем становится больше его. При условии обратимости процесса в диффузоре работа, затрачиваемая в нем на сжатие потока от рІ до р2, Очевидно, равна по абсолютной величине располагаемой работе при течении потока в насадках (соплах), но противоположной по знаку, т. е. /дИф = —/о - Следовательно, работа, затрачиваемая в диффузоре на сжатие газового потока, изобразится в системах координат р, V и Т, S (см. рис. 1.23, 1.24) площадями Ь21а и BdABeb соответственно. Направление изображенных на этих графиках процессов — против часовой стрелки, причем процесс 2-1 на ри-диаграмме — сжатие газа в диффузоре. Работа, затрачиваемая на сжатие парового потока в диффузоре, изобразится в координатах Т, S (см. рис. 1.25) площадью 21сЬе2, а в координатах /і, S (см. рис. 1.26) — отрезком 2-1, причем линии 2-І в обеих системах координат изображают процесс адиабатного сжатия пара.
Диффузор является основной частью турбомашин (турбокомпрессоров и турбонасосов), служащих для сжатия рабочего тела и транспортирования его потребителю.
Смешение газов. Рассмотрим смешение газовых потоков и смешение газов при наполнении резервуаров.
Смешение газовых потоков. Пусть п потоков с различными параметрами соединяются в один поток. При адиабатном течении газов без совершения внешней работы в соответствии с формулой (1.147) полная энергия потока газовой смеси равна сумме полных энергий по-
/ = п І = и
Токов, составляющих смесь, т. е. MCMhCM + MCMcM/2 = £ Mjii + ]Г m,-cf/2.
І = І і = і
Для большинства технических задач по причине малых скоростей течения можно пренебречь кинетическими энергиями по сравнению со значениями энтальпий соответствующих потоков. Тогда можно написать, что
І = П І—П
MCJicM= £ mfci, или HCM = £ GJh. (1.176)
І=1 1=1
Это уравнение справедливо для потоков идеальных и реальных газов, паров и жидкостей. Для идеального газа H = срТИ поэтому для него
І = и
Уравнение (1.176) запишется так: cpCMTCM = ]Г откуда
Г = 1
І~п І~п
Z QiCpiTi 2 QiCpiTi = - . (1.177)
Е в**
І = і
Объем смеси идеальных газов определится из уравнения состояния. Смешение идеальных газов при наполнении резервуаров. В резервуаре объемом VНаходится тх кг газа при рх и Тх. В него поступает т2 кг другого газа с параметрами р2 и Т2. После этого в резурвуаре будет тш кг смеси объемом VCM = V. Так как смешение газов происходит без производства внешней работы, то тсмиш = тхих + 4- т2и2.
Так как для идеального газа и = CvT, то
"WrcM^M = mCviTx Л - m2cv2T2,
Или
(mi/шсм) cvlTx 4- (т2/тсм) cv2T2 gxcvlTx + g2cv2T2 n 1по. JCM — ^ — . # ^ j[ /gj
Сгсм G{cv 1 + g2cv2
По известным Тсм и VCM определяются остальные параметры смеси.

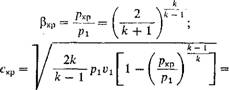
 Опубликовано в
Опубликовано в