ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С ЭЛЕКТРИЧЕСКИМИ ДУГАМИ
 26 июня, 2016
26 июня, 2016  admin
admin В предыдущем разделе рассматривался установившийся режим электрической цепи, а соответствующие расчеты выполнялись с помощью уравнения динамической характеристики (7.10), справедливого, вообще говоря, только для установившегося режима. Аналогично изложенному выше можно получить соответствующее выражение для динамической характеристики в переходном режиме, содержащее бесконечные ряды функций (гармоник). Однако как непосредственный анализ этого выражения, так и соответствующие расчеты показывают, что при Ь » 1 высшие гармоники быстро затухают и, за исключением малых отрезков времени вблизи т = 0, поведение дуги хорошо описывается динамической характеристикой, которую после дифференцирования и логарифмирования можно представить в виде
du/dr = (u/i)(di/dT) - bu(u - 1), (7.14)
где і - некоторое безразмерное значение тока дуги (например, ток дуги, отнесенный к току короткого замыкания і ). Следует отметить,
что в (7.14) не входит неизвестная величина (т. е. Л^), однако является неопределенной величина и{0)/і (0), т. е. безразмерное сопротивление разрядного промежутка в начальный момент времени = = которое необходимо рассчитывать каким-либо методом или
задавать по экспериментальным данным.
Совместное решение дифференциальной вольт-амперной характеристики (7.14) и системы дифференциальных уравнений электрической цепи при заданных начальных условиях позволяет без каких-либо итерации рассчитать переходный и установившийся режим цепи.
|
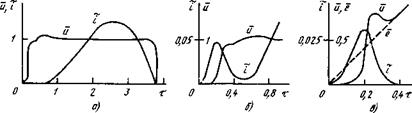
Рис. 7.6. Формы кривых напряжения и тока дуги при а = 2; Ь = 50; ф - 0: |
а, б) /?0 - кГ4; в) Л0 = 10 3
Рассмотрим цепь, в которой дуга включена последовательно с индуктивностью. Эта цепь описывается уравнениями
du/dr = (и/і)[asin(r + ф) - и] - bu(i? - 1);
di/dr = asin (т ♦ ф) - и,
где фаза ф определяет момент времени, в который возникает дуга и начинается переходный процесс. Начальные условия и(0) = /(0) = 0; и(0)/і (0) = /?Q. Система уравнений вместе с начальными условиями
решалась численным методом Рунге-Кутта.
Как и следовало ожидать, устойчивость горения дуги после поджига Зависит от а, ф и R^. На рис. 7.6 показаны кривые и и і для а = 2, 6 = 50, ф = 0 и двух значений /?Q. При /?Q = КГ4 переходный
процесс приводит к устойчивому горению дуги. Однако, рассматривая начало процесса более подробно (см. рис. 7.6, б), можно заметить, что дуга находилась ”на грани погасания”. Ток, который сначала быстро возрастал, стал убывать, а напряжение, уже было принявшее постоянное значение, стало увеличиваться. Но, пройдя минимальное значение, ток снова стал увеличиваться, напряжение дуги снизилось, и в дальнейшем переходный процесс привел к установившемуся режиму
— —з
горения дуги. Совершенно другая картина при /?Q = 10 (см. рис.
7.6, в). В этом случае дуговой разряд неустойчив. Ток, достигнув максимального значения при т - 0,2, резко, уменьшается, а напря
жение на дуге стремится к ЭДС, показанной штриховой линией. При т > 0,4 / =0 и и asin т, т. е. дуга погасла.
Таким образом, RQ существенно влияет на устойчивость дуги в
переходном режиме. Отметим, ЧТО критическое значение /? , при ко
тором происходит погасание дуги, зависит от параметров а и Ь. При Ь - 0 дуга устойчива всегда, так как в этом случае ее сопротивление постоянно во времени. С ростом Ь устойчивость дуги при заданных а и /?0 уменьшается. Увеличение а делает дугу более устойчивой.
 Критическое сопротивление зависит, конечно,
Критическое сопротивление зависит, конечно,
мально при ф = тг/2.
Отметим, что метод установления позволяет проводить расчеты при очень больших значениях Ь, чего не удавалось сделать методом итераций. Соответствующие расчеты показали, что форма кривой и(т) все более приближается к прямоугольной, но пик зажигания остается и сохраняется его величина. Однако он становится все более узким и
з
сдвигается к началу полупериода. В частности, при а = 4, Ь = 10
— —4
величина и достигается в момент времени т * 5е 10 , очень близкий /л
к началу полупериода. Если ввести понятие полуширины пика зажигания, т. е. такого отрезка времени г, в течение которого напря-
п
жение снижается в 2 раза по сравнению с и, то получим т =
—3 п
= 3*10 , что составляет ничтожную долю по сравнению с длительностью полупериода, равной я.

 Опубликовано в
Опубликовано в