Возникновение различных систем счисления (кодов) связано со стремлени­ем придать коду какие-либо дополнитель­ные свойства: обеспечить большую рав­номерность ввода информации в управ­ляющие устройства станком, упростить преобразование чисел из одной системы счисления в другую (из одного кода в другой), упростить вычислительные опе­рации, придать коду свойства обнаруже­ния или исправления ошибок и др.

Принцип самодополнения. Двоично - десятичные коды 2421, 4221 и 8421 с из­бытком 3 (табл. 1.4) называются само­дополняющимися. В этих кодах двоичное обозначение десятичной цифры А может быть получено из кодового обозначения цифры, равной 9— А (девять минус А) Путем простой инверсии знаков, т. е. заменой всех нулей единицами и наобо­рот. Так, в коде 2421, например, цифра 7 — 1101 — получается инверсией циф­ры 2 — 0010, цифра 4 — 0100 — инверси­ей цифры 5— 1011 ит. д.

Пример:

1101 — 7 0100 — 4 0001 — 1 0011—3

0010 — 2 1011 — 5 1110 — 8 1100 — 6

1111—9 1111—9 1111—9 1111—9

Этим же свойством обладает код 8421 с избытком 3 (8421 +3), в котором каж­дая десятичная цифра представляется суммой десятичного числа и,- и числа 3, выраженного в двоичном коде. Например, изображение цифры 5 в коде 8421 +3 — — 1000 соответствует изображению циф­ры 8 (5 + 3) в коде 8421 и т. д.

Указанное свойство кодов позволяет достаточно просто строить реверсивные двоично-десятичные счетчики управляю­щих систем станков и вычислительных устройств и вводить информацию в до­полнительном коде, т. е. вместо числа А записывать число 9 —Л. В ряде случаев это свойство может быть использовано для построения схем контроля.

Таблица 1.4. Изображение десятичных цифр в двоично-десятичных кодах 8421 +3 с N/w 8421 8421 +3 2421 4221 5211 (6) (4) (-2) (-1) Проверочной позицией 0 0000 ООП 0000 0000 0000 0000 10011 1 0001 0100 0001 0001 0001 0111 00100 2 0010 0101 0010 0010 ООП 0110 10101 3 ООП Оно ООН 0101 0110 0101 10110 4 0100 0111 0100 1000 0111 0100 00111 5 0101 1000 1011 0111 1000 1001 01000 6 0110 1001 1100 1010 1001 1000 11001 7 0111 1010 1101 1101 1011 1111 11010 8 1000 1011 1110 1110 1110 1110 01011 9 1001 1100 1111 1111 1111 1101 11100

Из приведенных самодополняющихся кодов код 2421 при прочих равных усло­виях имеет преимущество благодаря бо­лее простому преобразованию в двоич­ный код. В этом коде двоичные обозна­чения первых пяти цифр (от 0 до 4) совпадают с обозначениями этих цифр в нормальном двоичном коде 8421. Обо­значения же цифр от 5 до 9 в коде 2421 соответствуют обозначению в коде 8421 той же цифры (числа), но с избытком 6. Например, цифра 5 в коде 2421 обозна­чена 1011. Такое же обозначение в коде 8421 имеет число 11, т. е. число, равное 5 + 6. Цифра 7 в коде 2421 обозначается 1101. Это же обозначение в коде 8421 имеет число 13 (7 + 6) и т. д.

Помехозащищенность кодов. Особым свойством ряда кодов является помехо­защищенность. Это позволяет уже на эта­пе кодирования информации предусмот­реть возможность обнаружения или ис­правления разнообразных ошибок (или то и другое вместе): ошибки програм­миста, ошибки оператора, сбоев перфо­рирующих и считывающих устройств и т. д.

Коды, построенные в соответствии с принципами помехоустойчивого коди­рования, называют помехоустойчивыми. Кратностью ошибки называют число иска­женных символов в комбинации. Разли­чают коды, обнаруживающие ошибки, и коды, исправляющие ошибки. В зави­симости от кратности ошибки в том и дру­гом случае различают коды, обнаружи­вающие или исправляющие единичные ошибки, двойные ошибки и т. д.

Во всех случаях помехоустойчивость достигается ценой избыточности кода. Общая длина кодовой комбинации поме­хоустойчивого кода, равная п, представ­лена из двух частей. Одна часть содержит K комбинаций и служит для передачи не­обходимого сообщения. Такие комбина­ции называют информационными. Вто­рая часть содержит оставшиеся п — K Комбинаций и служит для обнаружения или исправления ошибок. Эти комбина­ции называют контрольными. Таким об­разом, для передачи сообщения исполь­зуют 2к комбинаций, которые называют разрешенными. Остальные (2П — 2к) ком­бинации для передачи сообщения не ис­пользуются и при нормальной работе устройства появляться не должны, их называют запрещенными.

При формировании кодов чаще всего деление всех кодовых комбинаций на информационные (разрешенные) и конт­рольные (запрещенные) осуществляется по четности или нечетности комбинаций , 0011

| 0 0} 0 1

Т2

Oil ГГ1

Т2

Т2

10

Ошибки нет

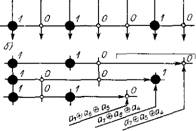
Рис. 1.4. Помехозащищенность кодов по чет­ности: а — передача разрешенной комбинации (четная); б — неразрешенная комбинация (нечетная — ошибка в передаваемом сигнале)

Из символов кода. При этом назначение комбинаций двух видов может быть раз­личным, хотя чаще всего разрешенными принимаются четные комбинации, так как при этом более просты контрольные устройства, обнаруживающие ошибки [6, 73]. Например, если для кодирования информации принята четная группа ком­бинаций (группа А), то нечетная группа комбинаций (группа Б) будет контроль­ной — запрещенной.

Четные комбинации (группа А): 0000; 0101; 0110; 1001; 1010; 1100; 1111.

Нечетные комбинации (группа Б): 0001; 0010; 0100; 0111; 1011; 1101; 1110.

Четные комбинации используют для передачи сообщений. Все нечетные ком­бинации являются запрещенными и при нормальной работе появляться не дол­жны. Появление нечетной комбинации обнаруживает однократную ошибку (ис­кажение одного разряда четной комбина­ции дает нечетную комбинацию). Это просто обнаруживается системой контро­ля, построенной, например, на логиче­ских элементах с функцией сложения по модулю m2 (рис. 1.4).

Б)

0001

Т.2

С контролем по нечетности составлен код 8421+3 с проверочной позицией (см. табл. 1.4). Левая (пятая) дорожка кода, являясь контрольной, слу­жит для дополнения знаком 1 кодовой комбинации в том случае, если число единичных символов (отверстий) основ­ной тетрады — четное. Таким образом, в коде разрешенными комбинациями яв­ляются нечетные. Появление комбинации с четным количеством единичных сим­волов, например 00101, 01111 и др., ука­
зывает на ошибку. Для сравнения ука­жем, что в незащищенном коде 8421 искажение одной позиции в какой-либо комбинации — например, вместо 0111 (десятичная цифра 7) передана инфор­мация 0110 (десятичная цифра 6) — приводит к переходу одной комбинации в другую и не позволяет достаточно про­сто обнаружить ошибку.

Метод контроля по четности или по нечетности комбинаций может осуще­ствляться не только по каждой комби­нации кода, но и по всему коду в целом. Таким свойством обладают некоторые равновесные комбинаторные коды, в частности 2 из 5 и 3 из 5. Десятичные цифры в этих кодах выражаются или двумя символами 1 (код 2 из 5) или тремя (код 3 из 5), которые своим положением на разных позициях определяют ту или иную цифру. Так, в коде 2 из 5 нуль кодируется 11000, единица — 00011, двойка — 00101 и т. д., т. е. в каждой комбинации, определяющей десятичную цифру, обязательно находится два сим­вола 1. Поэтому, если используется этот код, при появлении сигналов 01101, 01000 и других с количеством единиц менее или более двух сразу фиксируется ошибка. Однако код, как и многие другие имеющие помехозащищенность по попе­речной четности, не позволяет наити ошибку, если смещены единицы в преде­лах одной кодовой комбинации (напри­мер, вместо 01001 передана комбинация 00101), т. е. совершена двойная ошибка (0 вместо 1 на четвертой дорожке и 1 вместо 0 на третьей). Для определения двойных ошибок существуют соответ­ствующие коды и методы контроля [6, 73].

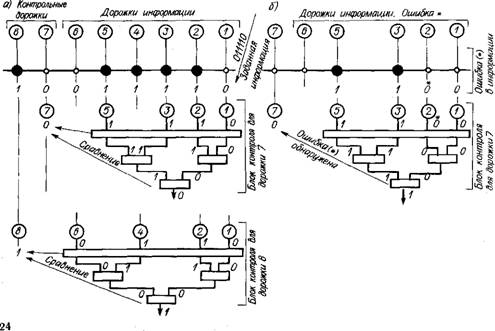
Рис. 1.5. Помехозащищенность кодов по нечентности (код AEG): а — перяда - ча разрешенной комбинации и ее конт­роль; б — ошибка в передаче

Большой класс корректирую­щих кодов составляют систематиче­ские коды, у которых значение контроль­ных разрядов получается в результате проведения операций над информацион­ными разрядами. Так, в коде AEG для металлорежущих станков для передачи информации используют кодовые комби­нации с длиной / = 8. На дорожках 1 — 4 (рис. 1.5, а) перфоленты записываются цифры в двоично-десятичном коде 8421, дорожки 5 а 6 служат для индексации чисел или букв, а дорожки 7 и 8 являются контрольными. На дорожке 7 указывает­ся (пробивается) символ 1, если число единиц на дорожках 1—3, 5 четное. Аналогично пробивкой на дорожке 8 сим­вола 1 дополняется до нечетного значе­ния число единиц, записанных на дорож­ках 1, 2, 4, 6. Такой контроль по нечет­ности одновременно по двум группам од­ной кодовой комбинации дает возмож­
ность обнаруживать 100 % одиночных ошибок и до 70 % всех возможных двой­ных.

Например, при записи на дорожках 6—1 (рис. 1.5, а) кодовой комбинации 011110 на дорожках 7 и 8 будет соответственно 0 и 1. Кодовые комбинации по группам дорожек бу­дут нечетные: дорожки 7, 5, 3, 2, I — 01110; дорожки 8, 6, 4, 2, 1 — 10110. Таким образом, для информации данной строки разрешенным будет сигнал 0 на дорожке 7 и сигнал 1 на дорожке 8, что и служит основой контроля передаваемой закодированной информации, построенной, например, на равнозначности (см. логические элементы в табл. 1.3, п. 5).

При появлении ошибки (например, на дорожке 2 вместо 1 будет прочитан 0 — рис. 1.5, б) сигнал контроля не будет соответ­ствовать записанному на контрольной дорож­ке. В данном случае на выходе контрольного блока будет 1, а на дорожке 7 будет 0. Это и укажет на наличие ошибки.

Надежная помехозащищенность осу­ществляется в семиразрядном ко­де, именуемом кодом 7,3. В нем для пере­дачи информации из семи разрядов (условно обозначим их ai — а7) исполь­зуются четыре разряда: а4 — aj. Три раз­ряда — а | — аз — являются контроль­ными, их значения вычисляются по фор­мулам:

Fli =а7©а5® а4; а2 = а7фа6фа4; а3 = а7(В

Фа6фа5-

При записи информации вычислен­ные значения ai—аз наносят на соответ­ствующие контрольные дорожки. На­пример, задаваемой информации 1010 (дорожки 4 — 7 на рис. 1.6) соответству­ют знаки 010 на контрольных дорожках 1—3. Эти знаки получены расчетом.

В системе управления при считыва­нии передаваемой информации для обна­ружения возможной ошибки использует­ся блок контроля. С помощью его логи­ческих элементов (сложение по модулю Т2) решаются уравнения обозревателя:

Д| = а? ©05 + ^4 + 01; Д2 = Q7 ф Об + 04 ф

Фа2; Аз = 07 © аб © as Ф аз.

Если при решении уравнений величи­ны Ai—Дз равны нулю, то ошибка отсут­ствует, в противном случае число на до­рожках 1—3 укажет номер разряда, в ко­тором допущена ошибка, и это даст воз­можность ее исправить. Как видно из уравнений обозревателя, при значениях

А1 = 1 и Л2=1 ошибка — в разряде а4, при Ах = 1 и Д3=1 —в разряде <25, при Л2= 1 и Лз= 1 — в разряде at,, при Ai= 1, Л2=1 и Дз — 1—ошибка в разряде ат.

Передадаемая информа- Сигналы контроля 1010 ция 010

G) Ошибка (*) 6 сигнале информации Сигнал контроля То 75 Ttf1 То ж? То1

(разряв а5)

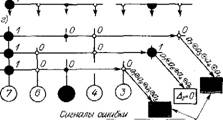
Рис. 1.6. Схема контроля информации в коде 7, 3: а — передаваемая информация и сигналы контроля; 6 — схема организации (расчета) контроля; в —- передача информации с ошиб­кой; г — схема контроля информации

Рассмотренные коды, осуществляю­щие контроль по поперечной четности, достаточно надежны. Но используют и другие виды контроля кодируемой инфор­мации: по продольной четности, по моду­лю, контроль кадра на кратность 3, 9 или 10 и т. д.

Контроль по модулю основан на проверке кратности суммы чисел, за­писанных на нескольких строчках в пре­делах некоторого завершенного объема комбинаций (например, в объеме кадра программы), некоторому числу т (моду­лю). В общем случае

^ Xi = g (mod т),

Где Xi — числовое значение кодовой ком­бинации, записанной в г-й строке; I — число строк в контролируемом объеме

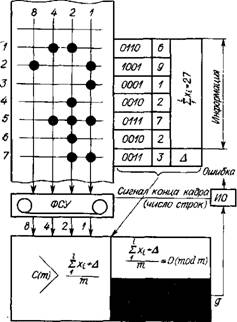
Рис. 1.7. Схема контроля по модулю т

Записанной информации; G — остаток от

/

Деления суммы J^X, на т.

1

Для того чтобы при любых значениях суммы по модулю С (т) сумма числовых значений, записанных в контролируемом блоке строк, была кратна величине т, Она дополняется некоторым числом Д, которое определяется при расчете инфор­мационных данных и записывается в том же коде на контрольной строке в преде­лах блока контролируемых строк: А = = M — G. При этом

I

£х, + Д = [Д + g] (mod т). (1.5)

1

Если A--g — m, То

I

^ +Д = 0 (mod т.).

1

Соотношение (1.5) является алгорит­мом контроля записанной информации по модулю т.

Пример. Шесть последовательно записан­ных строк информации (рис. 1.7) контроли­руются по модулю, например по т = 10. Для расчета контрольного числа последовательно суммируются числовые значения записанных на всех шести строках комбинаций (напри­мер, в коде 8421): ОНО, 1001, 0001, 0010, 0111, 0010, т. е. определяется сумма написан­ных в коде десятичных цифр. Следовательно,

Б

£Лг1. = 6 + 9+ 1+2 + 7 + 2 = 27.

Дополнением суммарного числа 27 до чис­ла, кратного модулю 10, будет число 3, кото­рое и является контрольным и записывается на седьмой строке данного контролируемого объема информации. Естественно, что инфор­мация, записанная на последующих шести строках, будет контролироваться по другому контрольному числу, рассчитанному для этих последующих строк, и т. д. по всему общему объему информации, которая программиру­ется.

В настоящем примере используется одна из возможных схем контроля, когда записан­ная информация с помощью читающего бло­ка ФСУ последовательно (построчно) подает­ся в специальный счетчик по модулю С (т). В счетчике информация суммируется. При по­лучении количества сигналов, численно равно­го модулю, счетчик автоматически начинает отсчет с нуля. Если прочитанная информация не имеет ошибок или прочитана без ошибок, то, получив количество сигналов (сумму чи­словых значений строк + контрольное число), кратное модулю, счетчик будет в нулевом состоянии. Состояние счетчика обычно опра­шивается сигналом от читающего устройства, который выдается после прочтения заданного для контроля количества строк. Если заданное количество строк равно семи (включая стро­ку с контрольным числом), то проверка пра­вильности информации будет выполняться после прочтения каждых семи строк в данном объеме всей информации. Если состояние счетчика отлично от нуля в момент контроля, то через индикатор ошибки (ПО) выдается сигнал о наличии ошибки.

Рассмотренный метод контроля доста­точно надежен. Так, если контролю под­лежит объем информации, записанной на 15 строках, то вероятность появления однократной ошибки составляет 0,9-10~2, двукратной — 0,4-10~4, трехкратной — 0,2-10~6. Как показывает анализ [6], одиночная ошибка при использовании рассматриваемого метода не обнаружи­вается, если ее числовое значение равно или кратно модулю т. Двойные ошибки не обнаруживаются контролем, если сум­ма числовых значений одиночных ошибок равна или кратна модулю или равна нулю.

Материальные носители информации для станков с ЧПУ — программоносите­ли — можно условно разделить на внеш­ние и внутренние.

К внешним программоносителям от­носят: перфокарты, перфоленты, кино­пленки, магнитные ленты, магнитную проволоку, магнитные барабаны и диски. Внутренние программоносители — это штекерные панели и коммутаторы, пане­ли с переключателями или кнопками, электронно-лучевые трубки и др. Внеш­ние программоносители можно быстро заменять, записывать на них программу и хранить отдельно от устройств ЧПУ, достаточно просто дублировать путем вы­полнения копий, использовать в однотип­ных устройствах и т. п. Внутренние программоносители обычно являются не­отъемлемым элементом конкретного УЧПУ, конструктивно с ним связанным.

Все программоносители характери­зуются по емкости, скорости записи ин­формации на них и скорости считывания этой информации, по быстроте замены, долговечности, удобству хранения, стои­мости.