Инженерная методика расчета воздушных завес, получившая рас­пространение в настоящее время, основана на применении условного коэффициента расхода воздуха через проем, защищенный завесой. Зная из эксперимента зависимость этого коэффициента от расхода воздуха, подаваемого в завесу и проходящего через проем в помещение, можно подобрать производительность и геометрические характеристики завесы. Все зависимости представлены в безразмерном виде. Наиболее поЛно эта методика изложена в работах В. М. Эльтермана и в «Указаниях но расчету воздушных завес».

Методически интереснее рассмотреть работу воздушной завесы с позиций струйной теории.

Воздушная завеса у проема в наружном ограждении — это плоская неизотермическая струя, развивающаяся на границе двух сред, имею­щих разную температуру. Перепад давлений снаружи и внутри помеще­ния приводит к изменению положения оси струи. Исследование плоских струй проводилось многими авторами. При определенных допущениях, о которых сказано ниже, можно воспользоваться теорией струй для оп­ределения характеристик воздушной завесы.

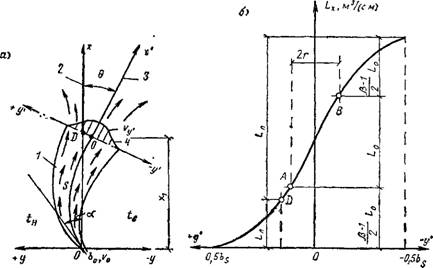
Рис XIX 6 Определение расхода воздуха в части сечения струи воздушной завесы A — схема струи 1 — струя, 2 — вертикальная плоскость, разделяющая струю, 3— направле ние оси струи в точке О; 4 — распределение скоростей в сечеиии струи, б — график изме­нения расхода воздуха в струе при перемещении вертикальной плоскости по сечеиию струи

Определение расхода воздуха в части сечения струи. Рассмотрим струю воздушной завесы (рис. XIX.6, a). Вертикальная плоскость, сов­падающая с плоскостью открытого проема, делит струю на две части Поток воздуха в струе подходит к этой плоскости под некоторым углом Э Расположим вспомогательную систему координат х'Оу' так, чтобы ось у' была перпендикулярна касательной к оси струи и проходила че­рез кромку открытого проема (точка D). Ось х'— касательная к оси в точке О. Допустим, что точка D, в которой происходит деление струи, находится на расстоянии у' от точки О А сама точка О расположена на расстоянии 5 от начала рассматриваемой струи вдоль ее оси

Расход воздуха, м3/(с-м), в части сечения струи в плоскости у'у' слева от точки D:

J Vy. dy(XIX. 2) 0,5 bs

Расход воздуха в части сечения струи справа от точки D в той же плоскости

Ln =-Ls —(XIX.3)

Где Ls — расход воздуха в сечении струи, находящемся на расстоянии S от ее на­чала в пределах 0,56s>«/'>—0,5&s (здесь &s — ширина струй, равная 0,416 S).

Распределение скоростей воздуха в сечениях струй воздушных за­вес изучено недостаточно. Есть утверждение В. М. Эльтермана, что да­же при значениях угла в >30° профиль скоростей в струе воздушной завесы соответствует профилю скоростей, характерному для свободных струй. Поэтому для решения нашей задачи воспользуемся формулами для плоских свободных струй. Распределение скоростей Vy' в сечении струи схематично показано на рис. XIX.6, а.

Если перемещать точку деления потока с левого края струи впра­во, то изменение расхода Ьл можно представить в виде графика, изоб­раженного на рис. XIX.6, б. В точке А плоскость делит струю на части, расход в которых составляет:

Ft — і _ р — і 1лА= 2 Ь0 И LnA = LO+ 2

А в точке В — на части, расход в которых равен:

Г. Р-1, г Р-1 ,

Л в — L0 2 0 И пВ ~~ 2

Здесь р — коэффициент увеличения расхода воздуха в струе

Р = LS/LQ = 0,536 yW>0 (по В. А. Бахареву),

Где Lo и bo — соответственно секундный расход воздуха на 1 м длины щели и ши­рина щели. *

Величина ^ lL0 соответствует расходу воздуха, подмешивающего­ся с одной из сторон струи до сечения у'у'.

Характерно, что между точками А и В проходит расход воздуха, численно равный L0 (назовем эту часть струи «ядром струи»). Ширина «ядра» 2г — функция bQ и 5 — определена ниже.

Для определения расходов в левой и правой частях струи удобнее пользоваться формулами:

Ьл = Ял и Ln = PL0 fin, (XIX.4)

Где Вя и Ви — безразмерные коэффициенты, выражающие соответственно расходы 1л и Ln в долях Ls-

Для практических расчетов составлен график (рис. XIX.7), при пользовании которым следует учесть, что £п=1—Ял. Используя график, можно решить и обратную задачу: при заданных расположении плоско­сти и расходе Ln или La определить vQ и bQ для данного проема.

LiZh t

Определение температуры воздуха в различных частях сечения струи воздушной завесы. Распределение избыточных температур в лю­бом сечении плоской неизотермической струи можно описать формулой Шлихтинга:

О (у' V'5

Где ty — температура воздуха в точке с координатами х, у; £<» — температура окружающего воздуха; tx — температура по оси струи на расстоянии х от сечения на выходе из щели.

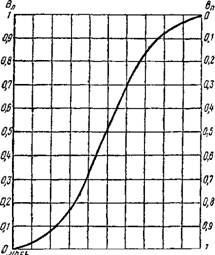
График изменения,&i'Q, x=f(y/J0,5bs) показан на рис. XIX.8, а.

Определение избыточной температуры в сечении струи в долях из­быточной температуры по оси в том же сечении—прием, распространен­ный при исследовании и расчетах неизотермических струй. Задача на­шего расчета — определение средней температуры в части сечения

А)

Ofi 0,к 0,2 0 -0,2 -0,6-0,8 - t/faSb

Im, -yW

У'т

у!0,5Ь

1,0

D)

Yy^iJ-rmTLl

-і

В)

-1

Рис. ХІХ.7. График для определения Рис. ХІХ.8. Распределение по сечению коэффициентов Вя и Вп неизотермической струи

А — избыточной температуры Ф/Ф,

Фициента Ро=Н

0ВИ0П

Струи, поэтому удобнее воспользоваться несколько иной формой записи зависимостей.

Примем за условный нуль отсчета температур too и введем коэффи­циент Ро, определяющий отношение избыточных температур:

T —t я у

Если за условный нуль отсчета принять температуру струи в сече­нии на выходе из щели to, то соответствующий коэффициент

Очевидно, что сумма этих коэффициентов равна единице. Оба они являются функцией х и у. Изменение ро в произвольном сечении струи - V показано на рис. XIX.8, б.

Используя эти коэффициенты, можно вычислить температуру воз­духа в любой точке струи по формуле

'„ = 1*0' О(Х1Х-6>

Здесь коэффициенты Ро и Роо имеют смысл долей единицы массы, по­падающих в точку (х, у) с температурой to и too. Значения р0 и рто мож­но вычислить по формулам для неизотермических струй.

Этот же принцип суперпозиции можно применить, рассчитывая tv для струи воздушной завесы. При разных температурах воздуха с двух сторон струи tn и tB и заданной температуре t0 можно определить влия­ние каждой среды на формирование температуры в любой точке произ­
вольного сечения струи, повторив рассуждения и введя аналогичные коэффициенты:

^ = Мо + Мн+Рв*в. (XIX.7)

Характер изменения значений коэффициентов р0, Рп и рв в произ­вольном сечении струи х, определенных с использованием их очевидных свойств, показан на рис. ХІХД б, в. Проведенные расчеты распределе­ния температуры по сечению струи воздушных завес показали, что влия­ние начальной температуры to с увеличением х быстро уменьшается. В сечении струи характерно резкое изменение температуры от tB на гра­нице с внутренним воздухом до tu на границе с наружным воздухом. Следовательно, средние температуры левой и правой частей струи (см рис. XIX.6, а) сильно отличаются друг от друга и от средней температу­ры по всему сечению струи. Последняя определяется из уравнения ба­ланса тепла в сечении х:

_ р — і р — і Рем ср ^см — U Ро cptо "Ь 2 ^о Рн cptн ~Ь 2 ^о Рв СР (XIX. 8)

Где рсмСр, роСр, рнср, рвср — удельная объемная теплоемкость воздуха при соот­ветствующих температурах.

Если Принять, ЧТО ПЛОТНОСТЬ воздуха рсм~р0~рн~рв, то из урав­нения (XIX.8) следует:

'см = у Св + tH). (XIX.9)

Средняя температура в части сечения струи рассчитывается по фор­муле, аналогичной формуле (XIX.7): в левой части сечения струи

^см л = Рол + Рн. л ^н + Рв. л tB> (XIX. 10)

В правой части сечения струи

^СМ-П = РоП h + Рн. П Рв-П ^В) (XIX .11)

Где ргЛ и ргп — средние интегральные коэффициенты по соответствующей части струи. .

Для практических расчетов значения р0л и р0п при длине оси струи S можно определить по формулам:

Рол = 3,12—?Ё=г; Реп = 3,12 , (XIX. 12)

VS/b0 Vs/b0

Где а0л и а0п — средние интегральные значения числового коэффициен­та (рис. XIX.9, а).

Значения рв. п и рн. п для расчета средней температуры правой части струи приведены на рис. XIX.9, б. Здесь x=S/bQ. Значения рвл и рнл можно определить по этому же рисунку, изменив шкалу y'/0,5bs на об­ратную.