В предыдущих разделах было показано, что форма кривой напря­жения на дуге даже в простейших цепях может существенно отличаться от синусоиды. Это приводит к некоторым особенностям измерений электрических величин. В частности, мощность дуги Р при отличной от нуля нелинейности дуги 6*0 нельзя вычислять как произведение эффективных значений силы тока и напряжения. Покажем это на сле­дующем примере.

Пусть кривая тока в цепи является синусоидой і - z^sin т, а

кривая напряжения имеет прямоугольную форму, т. е. |«(т)| = U = = const, где U - одновременно максимальное и эффективное значение.

Тогда измените мощности дуги во времени имеет вид Р(т) =

= t//^|sin т|. Среднее за полупериод значение мощности

7Г П

Р = Д - S Ui sin rdr = — Vi = Ul * 0.91//,

я m it m it

где / = / / J2 - эффективное значение силы тока.

Таким образом, в данном случае ошибка определения путем пе­ремножения эффективных значений I/ и / составляет 10 %. Расчеты показали, что при непрерывном^ горении (т. е. при а > 2) дуги с достаточно большим параметром Нелинейности ошибка составляет

10.. . 15 %, тогда как при горении дуги с паузами (т. е. при а < 2) ошибка может достигать 35 %.

Рассмотрим особенности измерения напряжений в трехфазных элек - тродуговых устройствах. Вольтметр электромагнитной, электродина­мической или тепловой систем, подключенный к электродам, между которыми горит дуга, покажет эффективное значение напряжения дуги. Поэтому измерение эффективных напряжений не представляет трудно­стей в тех устройствах, где дуговые разряды соединены между собой по схеме "треугольник”. При соединении дуг по схеме "звезда” могут встретиться два случая. Если в месте соединения дуг между собой расположен электрод (условно назовем его нулевым электродом), ко­торый доступен для электрического присоединения вольтметров, то измерение эффективных напряжений на дугах осуществляется соедине­нием вольтметров в "звезду", нулевой точкой которой является ну­левой электрод. Если параллельно вольтметру включить осциллограф, то можно получить истинную форму кривой напряжения на дуге (то же самое можно сделать и при соединении дуг треугольником). Однако на практике встречаются такие схемы электродуговых устройств (в частности, плазмотрон "Звезда"), в которых дуговые разряды сое­динены в звезду, но нулевой электрод недоступен для электрического присоединения измерительных приборов. В этом случае невозможно непосредственное определение напряжения на каждой из дуг и ис­тинной формы кривой напряжения на дуге. Тем не менее оказывается возможным косвенное определение искомых величин. Для этого

Рис. 7.18. Схемы соединения
вольтметров в "звезду" н "тре-
угольник"

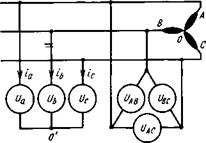вольтметры соединяют между со­бой в мзвезду” или в ’’треуголь­ник” (рис. 7.18), и по их пока­заниям с помощью поправочных коэффициентов можно найти иско­мые напряжения на дуговых разрядах. Ниже дается метод вычисления этих коэффициентов в случае симметричной нагрузки.

Известно, что вследствие нелинейности дуги как элемента элект­рической цепи разность потенциалов между точками О и О'(см. рис. 7.18) не равна нулю. Это легко показать. Обозначим мгновенные значения напряжений на дугах и на зажимах вольтметров:

и, = и ; и, = и.; и, = и ;

АО ° ВО ° СО С

Чд, Ug, Uq, а также uq, и^, и^, являются периодическими функциями,

сдвинутыми друг относительно друга на угол 2я/3. Имеем

и, = « - и. = и. - ив = и - иг (7.22)

CL А О В С С

I * L * і - О,

а Ь с

где і ; t - мгновенные значения токов, протекающих через вольтметры.

Поскольку сопротивление вольтметра является линейным элементом, то получим

и + и. + и =0. а о с

Совместное решение (7.22) и (7.23) дает 1

Таким образом, если и, * 0, то и. * и, uD * и., ип * и.

qq А а о ос с

Введем поправочные коэффициента к показаниям приборов:

*4 = "Л *4 ■ WUAB

Для других фаз получим аналогичные соотношения. При симмет­ричней нагрузке Uд = Uд - Ug поправочные коэффициента одинаковы

для всех трех фаз:

КС = К : КА = КВ = КС = К ‘

Выведем общие формулы для вычисления К и К. Согласно опреде­лению эффективного значения получим

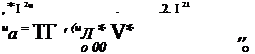Г 2

5 L—-л-

т|Л 2я ч

~ Т (“в * “сз *= "ST 17 ~ '

, 4з Г, 2.Г|/2

к' IF ' Vb*7 ' “А* •

42 О О

Аналогично находим

Для дальнейших преобразований представим периодическую функцию и(т) разложенной в ряд Фурье:

«(г) = Z A sin (nr + ):

л-о п п

А = — / u(r)dr; А = la2 + 62; tg ^ = - А - ;

О 7Г. П Ч П П П О

а = —/ «(г)cos птйт; л л 0

Ь = —/ «(r)sin лг</г. л л 0

Учитывая, что нагрузка фаз симметрична, имеем

ОО

и. = 2 A sin (яг + ф);

А л Л Л

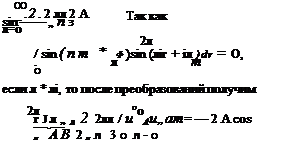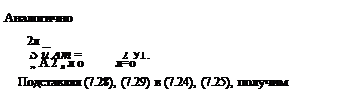п = о

1/2

 

оо

„ Л. 2 7ГЛ

Z Д sin —- л л з л=о

Так как біп2(ял/3) = 0, если л = Злі (т = 0, 1, 2, 3...) и 2

sin (ял/3) = 3/4, если л * Злі, то можно записать

л=о

Аналогично

/(' = — (1 - Ф) 1/2. (7.32)

4з

Формулы (7.30...7.32) позволяют вычислить К и /С в самом общем

случае, т. е. для любой формы кривой и(т). Проанализируем получен-

/

ные результаты. Из (7.30) и (7.32) следует, что К/К = ІЗ всегда, как и для обычных линейных цепей с симметричной нагрузкой. Это легко понять, если для объяснения воспользоваться принципом на­ложения, т. е. рассмотреть соотношение фазного и линейного напря­жений для каждой гармоники. Для гармоник, номера которых не кратны трем (л * Злі), фазные и линейные напряжения связаны соотношением

U = ІЗ U, а для гармоник с номерами л = Злі, а также для по-

Л ф

стоянной составляющей U^ = 0. Поэтому в разложении кривой линей­ного напряжения в ряд Фурье всегда отсутствуют постоянная состав­ляющая и гармоники с номерами л = Злі. Такой же вывод можно сделать относительно напряжения на вольтметре. Если разложение кривой фазного напряжения дуги и{т) в ряд Фурье не содержит гармоник с

номерами Злі, то, как следует из (7.31), Ф = 0, К = 1, К = 1/ІЗ. В

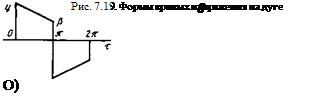общем Случае Ф > О, К > 1, К > 1/>Гз. Таким образом, погрешности в измерении напряжения связаны с наличием гармоник с номерами п = 3/л

в кривой напряжения дуги. Соотношение К/К = ІЗ показывает, что включение вольтметров в звезду или треугольник равнозначно с точки зрения точности измерении.

В предыдущих разделах были найдены формы кривых напряжения на дуге и(т) для некоторой упрощенной модели дуги. Вообще говоря, для стройности и последовательности изложения следовало бы восполь­зоваться именно этими кривыми и(т) для нахождения /С. Однако мы не будем этого делать по следующим причинам. Во-первых, эти кривые не выражаются аналитически, что усложняет расчет К; во-вторых, пред­ложенный метод расчета справедлив для любой формы и(т), в том числе и для напряжения на дуге с учетом конвекции, изменяющейся длины и т. д.; в-третьих, мы хотим дать лишь примеры расчета по­правочного коэффициента. Поэтому вычислим коэффициент К для формы кривой, изображенной на рис. 7.19, а, где /3 = и /и (и и и -

к и и к

начальное и конечное значения напряжения, т. е. и = и(0) и и =

н к

= и(я). При /3 = 1 получим типичную для многих дуг прямоугольную форму кривой напряжения. Разложение кривой (см. рис. 7.19, а) в ряд Фурье имеет вид

Расчеты показали, что при изменении & от 0 до 1 значение К ме­няется от 1,048 до 1,062, т. е. неучет нелинейного характера со­противления дуги при измерении напряжения дает в данном случае ошибку примерно в 5...6 %.

Однако при других формах кривой напряжения дуги эта ошибка может быть значительно больше. Например, для кривой рис. 7.19, б, состоящей из участков параболы, К = 1,14, т. е. ошибка достигает уже 14 %.

Таким образом, поправочные коэффициенты могут быть вычислены, если известна форма кривой напряжения дуги. Однако, например, в плазмотроне ’’Звезда” эта форма не может быть получена осцилло - графированием из-за отсутствия нулевого электрода. Искомая форма может быть рассчитана, если существует теория, соответствующая данному конкретному случаю. Форму кривей напряжения дуги можно получить и из формы кривой линейного напряжения путем некоторого пересчета, однако при одном допущении.

Пусть известна форма кривой линейного напряжения (ее всегда можно получить с помощью осциллографа)

ОО

где А и ф известны. Напряжения дуг запишем в виде л л

оо

и. = £ X sin (от + ф );

А л л л

л-о

оо

«п = 2 Xsin (яг + ф - - Щр - ),

D „Л Л 3

Л-О

где X и ip неизвестны. Так как и. п = и. - то л л АВ А В

оо

£ A sin (яг + ф ) = л Л л

л-о

оо

= £ 2Х sin cos (яг + ф - ).

л л 3 *л 3

л-о

Приращивая коэффициенты и углы, получим А

X =-------------------- •

Л 2sinjm/3 ’

Формула (7.36) соответствует разложению в ряд Фурье прямоугольной функции с амплитудой, равной 0,5.

Таким образом, получили кривую фазного напряжения, имеющую пря­моугольную форму, а значение этого напряжения в 2 раза меньше и. Непосредственным графическим построением можно убедиться в пра­вильности полученного результата.

Рассмотрим измерение активной мощности в трехфазной трехпро­водной цепи с дуговой нагрузкой методом двух ваттметров. Изме­ренное значение мощности

равно истинному, причем это справедливо и для несимметричной нагрузки.