Аэродинамический расчет воздуховодов обычно сводится к опреде­лению размеров их поперечного сечения, а также потерь давления на отдельных участках и в системе в целом. Это — прямая задача. Возмож­на и обратная задача — определить расходы воздуха при заданных раз­мерах воздуховодов и известном перепаде давления в системе.

При аэродинамическом расчете воздуховодов систем вентиляции можно пренебречь сжимаемостью перемещающегося воздуха, так как максимально возможное изменение давления в системе меньше 5% ат­мосферного. По этой же причине принято пользоваться значениями избыточных давлений, принимая за условный нуль атмосферное дав­ление на уровне системы. Одна из особенностей вентиляционных си­стем — наличие участков, где избыточное давление меньше нуля.

При движении воздуха по воздуховоду в любом поперечном сече­нии потока различают три вида давления: статическое, динамическое и полное.

Статическое давление определяет потенциальную энергию 1 м3 воз­духа в рассматриваемом сечении. Статическому давлению рст равно давление на стенки воздуховода.

Ptr

Динамическое давление — это кинетическая энергия потока, отне­сенная к 1 м3 воздуха. При скорости движения воздуха в сечении v ди­намическое давление

(XI. 1)

Полное давление равно сумме статического и динамического дав­лений

Рп = Рст+Рд. (XI. 2)

Традиционно при расчете систем трубопроводов применяется тер­мин потери давления-, необходимо помнить, что в действительности речь идет о потерях энергии потока. Единица потерь энергии, выраженных в удельных величинах (отнесенных к объему), совпадает с единицей давления. Например, в системе СИ единица давления паскаль (Па) соответствует Н/м2 и, следовательно, Н-м/м3, т. е. Дж/м3. В системе МКГСС давление измеряется в кгс/м2 (соответствует кгс-м/м3).

Потери давления в системе вентиляции складываются из потерь на трение и потерь в местных сопротивлениях.

Потери давления на трение. Рассмотрим движение воздуха на от­резке воздуховода (рис. XI. 1) между сечениями /—I и II—II. Заданы

Рис. XI. 1. Отрезок воздуховода длиной I и диамет­ром d (v — скорость движения воздуха)

Длина отрезка /, площадь поперечного сечения f, периметр сечения Я и расход воздуха, проходящего через воздуховод, L, м3/ч. Статическое давление в сечении I—I равно рі, в сечении II—II — рц<.рь

На объем воздуха, заключенного в воздуховоде между рассмат­риваемыми сечениями,, действует сила (pi—pn)f, уравновешиваемая си­лой сопротивления трения воздуха о стенки воздуховода.

Если обозначить касательное напряжение у поверхности стенки, возникающее при движении воздуха, то, то силу сопротивления можно определить так: то 1П. Следовательно, для установившегося движения

(Pi - Рц)/ = Vя» <Х1-3>

Отсюда

---------------------------------------------------------- ш------- • (*М)

Известно, что касательное напряжение пропорционально динами­ческому давлению перемещающейся среды:

Риа

Ч = ' (Х1-5)

Где ф — коэффициент пропорциональности, называемый коэффициентом трения к формуле Вейсбаха.

Сопоставляя выражения (XI.4) и (XI,5), получим формулу Вейс­баха, широко применяемую в гидравлике:

1П ру2

ДРтр = Pi = V - #1.0)

Отношение Д/У7 для воздуховода круглого сечения равно 0,25 d, т. е.

I pv2

Арір=Лтр — — . (XI. 7)

Эта формула предложена Дарси, а коэффициент Ятр = 4 называ­ют коэффициентом сопротивления трения. Формула Дарси для воздухо­водов с произвольной формой поперечного сечения

1П ри2

ДРтр=Я*р— у. (XI.8)

Коэффициент сопротивления трения в общем случае является сложной величиной, зависящей от режима движения воздуха в воздухо­воде и шероховатости стенок воздуховода:

Где Re — критерий Рейнольдса; К — высота выступов шероховатости (абсолютная шероховатость)-; значения К приведены в табл. XI.1.

Таблица XI.1 Абсолютная шероховатость К стенок воздуховодов из различных материалов Материал стенок воздухо­вода 1С. мм 1 Материал стенок воздухо­вода К, мм Листовая сталь. . . Шлакогипсовые плиты Шлакобетонные » Винипласт ........................ Кирпичная кладка (ка­налы в стенах) .... То же, со штукатуркой и протиркой поверхности I 0,1 1 1,5 0,1 5—10 3—6 Штукатурка по сетке. Асбестоцементные пли­ты или трубы.... Фанера...... Латунь, стекло. . . Резиновые рукава. . 10 0,11 0,1—0,3 0,0015—0,01 0,006—0,01

Для определения коэффициента сопротивления трения предложен ряд зависимостей, учитывающих характер движения и шероховатость стенок. Некоторые зависимости приведены в ч. I учебника. В настоящее время широкое распространение получила формула, предложенная А. Д. Альтшулем:

/68 , К »25

*,Р=о. п(-+т) , (XL9)

Эта формула универсальна и дает достоверные результаты для всех областей турбулентного режима движения. Единицы К и d в формуле (XI.9) принимают одинаковыми.

При инженерных расчетах потери давления на трение в воздухо­воде длиной I, м, принято определять по выражению, Па (кгс/м2):

Артр = RU (XI. 10)

Где R — потери давления на 1 м длины воздуховода, Па/м [кгс/(м2-м)].

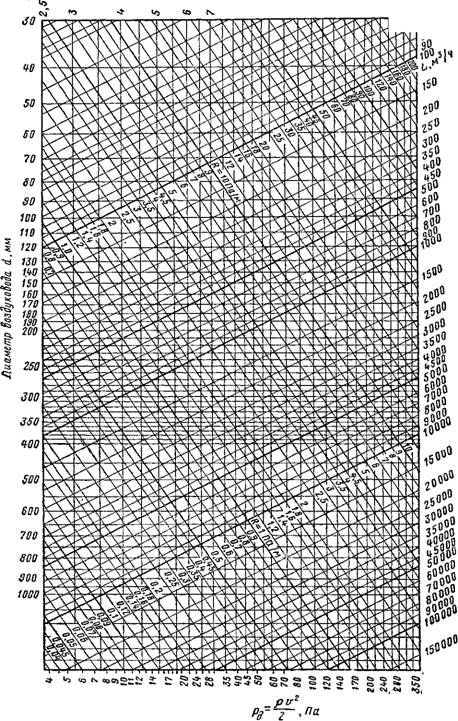
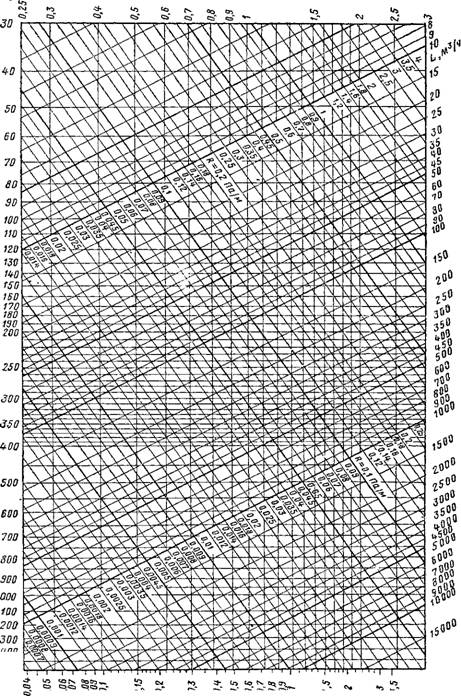
Для определения R составлены таблицы и номограммы (рис. XI.2)". При построении номограмм принято: форма сечения воздуховода — круг диаметром d, давление воздуха 98 кПа (1 ат), температура 20° С.

Для расчета воздуховодов и каналов прямоугольного сечения поль­зуются таблицами и номограммами, составленными для круглых возду­ховодов, но вводят при этом эквивалентный диаметр, при котором по­тери давления на трение в круглом и прямоугольном воздуховодах равны.

В практике проектирования получили распространение три вида эквивалентных диаметров: по скорости — dv, по расходу — dL и по пло­
щади поперечного сечения — df. Каждый из этих диаметров определен­ным образом связан с размерами поперечного сечения прямоугольного воздуховода а и b и для каждого имеется свой способ пользования расчетной таблицей или номограммой. Конечный результат (потери давления на трение в прямоугольном воздуховоде), естественно, не за­висит от способа определения эквивалентного диаметра.

Эквивалентный по скорости диаметр dv можно определить из усло­вия, что удельные потери на трение в круглом R и прямоугольном Rup воздуховодах равны при v = vTW.

Потери на трение в прямоугольном воздуховоде по формуле (XI.8)

Л ! 12 (" + Ь)ру* ,YI 1П

Дртр=Атр--------------------------------------------------- —------- — . (Л1.11)

4 ab 2

Потери на трение в эквивалентном круглом воздуховоде по фор­муле (XI.7).

I ру2

ДРтр==ЯТр — (XI .12)

Приравняв выражения (XI. 11) и (XI. 12), получим:

Dv = 2ab/(a+b). (XI. 13)

Чтобы найти значение Ящ, по таблице или номограмме, составлен­ной для круглых воздуховодов, необходимо определить R при dv и ипР (фактической скорости в прямоугольном воздуховоде), не принимая во внимание фактический расход воздуха.

Эквивалентный по расходу диаметр dL определяется из условия, что R=RII9 при равенстве расходов в круглом и прямоугольном возду­ховодах (L=Lnp).

Потери на трение в прямоугольном воздуховоде можно выразить через секундный расход воздуха:

4а6 <*)4- (Х1Л4)

Потери на трение в эквивалентном круглом воздуховоде

I р£2

Дртр = Ятр — ——-——■. (XI. 15)

DL (я4/4)22

1,265 1/ —т. (XI. 16)

Приравняв выражения (XI.14) и (XI.15), получим:

32 а*Ь*

Ь я2 (а + Ъ)

Или

Скорость іїоздуха. іг, м/с 1600 C»<f сэса Динамическое давлениер.--О—, Па.

Рис XI 2 Номограммы для определения потерь давления на трение в круглых воздухо-

А — при естественной вентиляции, б — при

Скорость Воздуха. V, м/с

Ю о S S Й § $ $ Ш*

Динамическое даблете

Водах (К— 0,1 мм) механической вентиляции

То 1200 1300 То 1500 1SW

Сечения df. Значение df определяется из условия равенства площадей сечения ab — nd2f /4:

Df = 2VabJn. (XI. 17)

Значение Ящ> в этом случае определяют по формуле

Rnp = Rm, (XI. 18)

Где R — табличное значение, принятое при df и v или L (по фактическим скорости или расходу); m — коэффициент учета формы воздуховода, определяемый по дополни­тельной таблице или графику.

При расчете воздуховодов с шероховатостью стенок, отличающейся от предусмотренной в таблицах или в номограммах (i(=0,l мм), следу­ет делать поправку к табличному значению удельных потерь давления на трение:

Яш = ЯРш, (XI. 19)

Где R — табличное значение удельных потерь давления на трение; {5Ш — коэффи­циент учета шероховатости стенок (табл. XI.2).

Таблица XI.2

Поправочный коэффициент р ш для расчета воздуховодов с различной шероховатостью стенок К ПРИ К, мм V, м/с 0,01 0,2 0,5 2 5 10 15 20 0,3 0,5 1 2,5 0,996 0,993 0,986 0,966 1,005 1,008 1,015 1,034 1,019 1,031 1,057 1,12 1,082 1,127 1,216 1,388 1,183 1,267 1,42 1,682 1,309 1,413 1,637 1,973 1,407 1,552 1,792 2,173 1,488 1,65 1,915 2,329 3 5 10 15 0,96 0,938 0,894 0,861 1,039 1,057 1,088 1,107 1,136 1,189 1,27 1,316 1,429 1,549 1,712 1,8 1,74 1,908 2,13 2,247 2,045 2,253 2,524 2,666 2,254 2,487 2,79 2,948 2,418 2,669 2,996 3,166 Пример ХМ» Определить d» и R для воздуховода с поперечным сечением 300X800 мм при расходе воздуха £ = 3500 м3/ч. Решение. 1. По формуле (XI.13)

Do= 2-0,3-0,8/(0,3 + 0,8) =0,436 м.

2. Скорость воздуха в воздуховоде

V = 3500/(3600-0,3-0,8) -4 м/с.

3. По рис. XI.2, б при вычисленных значениях dv и v найдем /?=0,4 Па/м.

Потери давления в местных сопротивлениях. В местах поворота воздуховода, при делении и слиянии потоков в тройниках, при измене­нии размеров воздуховода (расширение в диффузоре, сужение в кон - фузоре), при входе в воздуховод или в канал и выходе из них, а также в местах установки регулирующих устройств (дросселей, шиберов, диафрагм) наблюдается падение давления в потоке перемещающегося воздуха. В указанных местах происходит перестройка полей скоростей воздуха в воздуховоде и образование вихревых зон у стенок, что сопро­вождается потерей энергии потока. Нарушение установившегося поля скоростей начинается на некотором расстоянии до местного сопротив­ления, а выравнивание потока происходит на некотором расстоянии (обычно несколько калибров — диаметров) после него. На всем участке возмущенного потока происходят потери энергии на вязкое трение и увеличиваются потери на трение о стенки. Однако условно для удоб­ства проведения аэродинамического расчета потери давления в местных сопротивлениях считают сосредоточенными.

Потери давления в местном сопротивлении пропорциональны дина­мическому давлению воздуха в воздуховоде:

Коэффициент £ (дзета) носит название коэффициента местного со­противления и определяет потери давления в местном сопротивлении в долях динамического давления. Значения £ для различных местных сопротивлений изменяются в широких пределах — обычно 0<£<;10.

• При небольших скоростях движения воздуха и значительных потерях давления, например в диафрагме, коэффициент £ может быть очень вы­соким, порядка несколько сотен. В отдельных случаях в ответвлениях тройников возможен отрицательный коэффициент Это означает уве­личение удельной энергии потока ответвления вследствие эжекции его основным потоком. Таким образом, при расчете изменения давления следует учитывать знак

При определении потерь давления необходимо знать, к какой ско­рости относить коэффициент Обычно это наибольшая скорость в су­женном сечении участка или скорость в сечении участка с меньшим расходом (в тройнике). В таблицах коэффициентов местных сопротив­лений указано, к какой скорости относится

Потери давления в местных сопротивлениях участка, обозначае­мые z, равны:

Z = 2£рд, (XI. 21)

Где — сумма коэффициентов местных сопротивлений на участке.

Общие потери давления на участке воздуховода длиной I при нали­чии местных сопротивлений

Друч-ЯРш' + г, (XI. 22)

Где — потери давления на 1 м длины воздуховода; г — потери давления в местных сопротивлениях участка.