Сталезалізобетонні елементи є конструкціями, що складаються зі сталевої та залізобетонної частин. їх розрахунок виконують за зведеними

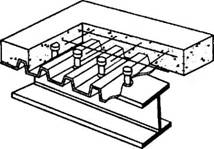
Рис. 11.6. Конструкція сталезалізобетонного Міжповерхового перекриття, що містить монолітну залізобетонну плиту, з'єднану зі сталевими профнастилом і балкою.

До сталі геометричними характеристиками, вико­ристовуючи коефіцієнт зведення

Е

Оь=вГ. (11-1)

Де Еь та Es — модулі пружності бетону та сталі відповідно.

Тобто зведена площа сталебетонного перерізу становитиме

Artd = — Ab + As, (11.2)

Аь

Де Аь і А„ — площі бетонної та сталевої частин перерізу.

Проектуючи сталебетонні конструкції, най­частіше мають справу з двотавровими перерізами (рис. 11.7). Верхня поличка сталевої балки сприй­має зусилля разом зі залізобетонною плитою, а тому приймається зменшеного перерізу. Водночас треба пам'ятати, що під час монтажу, коли залізо­бетонна плита ще не сприймає зусиль, важливо забезпечити стійкість стисненої (верхньої) полич­ки сталевої балки. Чимало аварій сталося саме під час монтажу сталезалізобетонних конструкцій через недостатню стійкість стисненої полички сталевої балки.

Визначаючи розрахунковий переріз, передусім обчислюємо розрахункову ширину звисів залізо­бетонних полиць, адже що далі від балки — то залізобетонна плита сприймає меншу частку від сумарних зусиль комплексного сталезалізобетон - ного перерізу. Розрахункові звиси залізобетонної плити (bf — між балками і bfc — для консолей) можна приймати за табл. 11.1 чи згідно з реко­мендаціями нормативних документів.

Таблиця 11.1

Розрахункові звиси плит Звис Проліт балки, L Ширина розрахункового звису Ь/ — у бік сусіднього елемента (балки) у ви­падку кількох пара­лельних балок >4В Bf = В/2 <4 В Ь/ = s + Ghf, але не більше В/2 і не менше 1/8 Ь/,с — консольний >12С Bf, с = С < 12С Bf, c = s + 6 h/-c, але не більше С і не менше 1/8 Де В і С — відстань між осями балок і конструктивне зна­чення звису залізобетонної плити відносно осі балки

Розрахунок проводять за зведеними до сталі балки геометричними характеристиками: поло­женням центра ваги, моментом інерції, моментами опору, статичними моментами частин перерізу тощо, які обчислюють з використанням коефіці­єнтів зведення (11.1) для відповідних частин перерізу, як це наведено в (11.2). При цьому на різних стадіях роботи беруть до уваги лише час­тини перерізу, що можуть сприймати зусилля: • перша стадія (період монтажу), коли все на­вантаження сприймається лише сталевою

F.EЈ

'0,5bfs2

Плита / Залі зобетОнна Аь

І °Ь2+СЬЗ

+ с'2 + а'3

І

Центр ваги бетонної плити

Центр ваги зведеного сталезалізобетонного перерізу для другої стадії

Центр ваги сталевого двотавра для першої стаді ї

Is

Сталевий двотавр А

А б в г Д

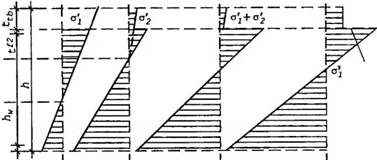
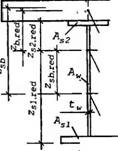
Рис. 11.7. Розрахункова схема сталезалізобетонного перерізу, що складається зі сталевого двотавра і залізобетонної плити (а); епюра напружень у першій стадії навантаження (період монтажу), коли залізобетонна плита не включена у роботу (б) — діють напруження від власної маси сталевої балки, залізобетонної плити, риштувань і опалубок, опертих на сталеву балку, а також атмосферних навантажень і впливів; епюри у другій стадії (в), стадія зведення — діють повне постійне, атмосферні та ін. навантаження і впливи; принцип додавання епюр напружень від першої стадії та навантаження, прикладеного у стадії 2 (г); сумарна епюра напружень у третій стадії (б); Аь, As — бетонна і сталева частини (Л5і, Лй, Asw — відповідно площі верхньої та нижньої поличок і стінки двотавра).

Балкою, а бетон монолітної плити чи швів між збірними залізобетонними плитами сві - жовкладений і не може сприймати зусиль;

• друга та третя стадії — бетон має міцність, достатню для сприймання зусиль, тобто пра­цює весь переріз сталезалізобетонної балки. При цьому враховують, що у другій стадії прикладено лише постійне навантаження і деформації у бетоні мають переважно пруж­ний характер, тобто коефіцієнт зведення (11.1) обчислюють за початковим модулем пружності бетону. У третій стадії, під час дії повного навантаження, переважають пластичні деформації та деформації повзу­чості бетону, що зумовлює зменшення його модуля деформування.

Варто зазначити, що крім силових факторів на напружено-деформований стан сталезалізобе­тонних конструкцій впливають явища зсідання та повзучості бетону. Окрім цього, через різну теп­лопровідність сталі й бетону (відрізняються приб­лизно у 50 разів) між частинами перерізу вини­кають суттєві різниці температур. Це змушує враховувати для сталезалізобетонних конструк­цій не тільки загальні зміни температури, а й різниці температур різних частин і точок кон­струкцій.

Добір перерізів сталезалізобетонних балок здійснюють шляхом послідовних наближень. Щоб зменшити кількість ітерацій, у першому набли­женні доцільно приймати переріз, припускаючи, що згинальні моменти сприймають переважно полички (сталеві та залізобетонні), а на сталеву стінку припадає лише частка згинального момен­ту — близько 20% для першої стадії і 5% — для другої. Окрім цього, у пружно-пластичній стадії, враховуючи розвиток пластичних деформацій у бетоні і пов'язаний з цим перерозподіл зусиль, розрахунковий опір сталі умовно збільшують на 15% для верхнього поясу і 5% — для нижнього.

Згідно з цим отримуємо такі рівняння:

= 1,15R„

S2

Mn

Де =

-1 + - JU 1,05K,;

Верхній пояс

N.

Нижніи пояс

А,

Asl +

Ab, ef

MJ

ЇЖ

L,05hsb

У поличках на першій і другій стадіях роботи; hs — відстань між центрами ваг перерізів ста­левих поличок; hsb — те ж, але між центрами ваг верхньої залізобетонної плити і сталевої

Es Ми

Нижньої полички; ОСь Pf = т=г '------------------------------- кое -

' Еь Мр + 0,35МдЯ

Фіцієнт зведення бетону з наближеним враху­ванням його повзучості; М,, Ми — згинальні мо­менти від навантажень і впливів на першій та заключній стадіях роботи; Мр — згинальний мо­мент від тимчасових навантажень; МдІІ — те ж від постійних та довготривалої частини тимчасо­вих навантажень у заключній стадії роботи.

Звідси площі поличок

N, + Nn

Місце дії напружен­ня	Характер напруження	Стадія
Перша	Заключна
Крайнє волокно сталевої нижньої полички S1	Розтяг	I Мі Osl = - j-Zs 1 Js	Її Ми Osl = у--- Zsl, red Jred
Крайнє волокно сталевої верхньої ПОЛИЧКИ S2	Стиск	1 М, Osl = - J-ZS2 Js	И Мп Os2 = - j-- ZS2. red Jred
Центр ваги Бетонної полички Ь	Стиск	Бетонна поличка відсутня	N Mil Ob = ---- 2b, red Jred
Де Js, Jred — моменти інерцій сталевої частини та зведеного перерізів; zsi, Zs2 — відстані від центра ваги сталевого перерізу до крайніх волокон відповідно верхньої та нижньої сталевих поличок; гь — те ж між центрами ваг зведеного сталебетонного перерізу й бетонної полички (наявність індек­су red свідчить, що значення приймають для зведеного ста­лебетонного перерізу)

(11.4)

Умовні осьові сили

Таблиця 11.2 Напруження від згинальних моментів

Дії - n ;

1.05R,,

JJ^ + 0,25Ад - 0,5АД, (11.6)

Де Ад =

L,15Ry '

Напруження у характерних волокнах прийня­того перерізу обчислюють за формулами табл. 11.2. При цьому у заключній стадії роботи балки де­формацію повзучості бетону можна не врахову­вати, якщо рівень його напружень невисокий — ob < 0,2R(„ де Rb — розрахунковий опір бетону стискові.

При вищих напруженнях беруть до уваги пе­рерозподіл напружень, зумовлений повзучістю бетону. У цьому випадку напруження від постій­ного та довготривалого навантаження з урахуван­ням повзучості бетону наближено можна обчис­лити в припущенні, що січний модуль деформацій ■ бетону (або, як його ще інколи називають, ефек­тивний модуль пружності бетону) EeIj = 0,35 Еь, як це зазначено вище для коефіцієнта аь ef.

У сталезалізобетонних конструкціях деформа­ції зсідання бетонної полички стримуються по­тужною сталевою балкою. В результаті виника­ють внутрішні напруження розтягу — у бетонній плиті і стиску — в прилеглих до неї сталевих частинах. При значних деформаціях зсідання (на­приклад, через порушення вологісних умов під час тверднення щойно вкладеного бетону чи інші причини) спостерігаються навіть наскрізні попе­речні тріщини у бетонній частині перерізу.

Оскільки центри ваг перерізів сталі та бетону не збігаються, то весь сталезалізобетонний еле­мент прогинається вниз і в протилежному від бе­тону волокні сталевого перерізу з'являються зде­більшого напруження розтягу. Окрім того, дефор­мації зсідання зумовлюють зсувні зусилля між бетонною плитою та сталлю, при цьому їх на­прямок протилежний до зсувних зусиль від зов­нішнього вертикального навантаження. Внаслідок стримувального впливу сталі остаточна дефор­мація зсідання плити суттєво менша за вільне зсідання бетону. Окрім цього, значна частина де­формацій зсідання збірної плити відбувається до з'єднання зі сталевою частиною. З достатньою для практики точністю вважають, що у монолітній плиті ця деформація становить Esh = 2 • 10~4, а у збірній, яка зазнала термовологої обробки — Єа = 1 • Ю"4.

Як вже зазначалося, в сталезалізобетонних конструкціях поєднано бетонні та сталеві елемен­ти, теплопровідність яких суттєво відрізняється. Це змушує брати до уваги не тільки загальні зміни температури, а й різницю температур у різ­них точках перерізу. Загальна зміна температури спричиняє переміщення опор внаслідок видов­ження чи вкорочення конструкції. Ці деформації обчислюють як звичайно для металевих чи залі­зобетонних конструкцій. Різниці температур між окремими точками перерізу виникають головно через те, що температура сталевої частини, яка має значно вищу теплопровідність і меншу теп­лову інерцію, ніж бетон, під впливом температури повітря і сонячного проміння змінюється швидше й у ширших межах. Аналіз результатів натурних вимірювань температур, теплофізичних розра­хунків та обчислення температурних напружень дав змогу відзначити три характерних варіанти розрахунку:

• перший варіант — підвищення температу­ри повітря та сталевої частини в поєднанні з нагріванням сонячними променями (найчастіше в ранкові години);

• другий варіант — швидке зниження тем­ператури (наприклад, під час дощу з градом) і відповідне охолодження сталевої частини;

• третій варіант — нагрівання сонячними променями залізобетонної плити (опівдні, коли сталева балка перебуває в тіні).

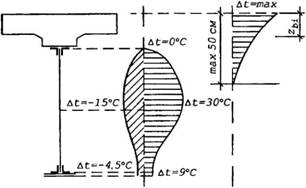
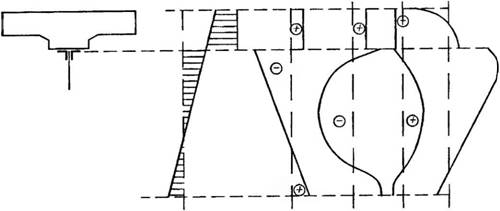
У розрізних балках перший варіант зумовлює напруження розтягу у бетонній плиті, що може супроводжуватися утворенням поперечних трі­щин (як від зсідання бетону). Для другого та тре­тього варіантів характерні переважно деформації стиску в бетоні. Щоправда, для третього варіанту при швидкому нагріванні верхньої грані плити со­нячним промінням на її нижній, затіненій (тобто холоднішій) поверхні спостерігаються напружен­ня розтягу і є небезпека тріщиноутворення саме у цих зонах плити. Рекомендовані критичні різ­ниці та аналітичні описи епюр температур у перерізах для кожного зі зазначених випадків по­дано у нормативній літературі. При цьому не­обхідно зазначити, що перелічені варіанти треба чітко узгоджувати з умовами зведення та екс­плуатації будівлі (наприклад, усі три варіанти найбільш характерні під час зведення будівель та експлуатації конструкцій на відкритому по­вітрі, при експлуатації навісів критичними є дру­гий і третій варіант тощо). Приклади нормативних епюр розподілу температур зображені на рис. 11.8, а зумовлені ними напруження — на рис. 11.9.

Беручи до уваги гіпотезу плоских перерізів, значення напружень, зумовлених зсіданням бе­тону та температурними впливами, можна обчис­лювати за залежностями табл. 11.3, 11.4.

Розрахунок міцності поперечних перерізів ста­лезалізобетонних конструкцій виконують за кри­терієм граничних деформацій. Повна пружно - пластична відносна деформація бетону на рівні центра ваги його перерізу обмежена значенням ЄЬ, lim = 1.6 " Ю-3. Для сталевих поясів граничні пластичні деформації становлять

Es, iim= 1.0' 1СГ3. Міцність сталевих поясів для спрощення перевіряють за традиційною формою перевірки напружень, але зі застосуванням по - правкових коефіцієнтів при моментах опору та розрахункових опорах, які зводять розрахунок до деформівного критерію граничного стану. Розра­хунок грунтується на гіпотезі плоских перерізів і методі тонкої плити. В граничному стані прий­мається пружно-пластична (або пружна) робота сталевого двотавра й пластична — бетонної плити. Дані для розрахунку міцності наведені у табл. 11.5 (розглядається лише випадок, коли бе­тонна плита стискається тимчасовим навантажен­ням).

Значний обсяг у розрахунках займають пере­вірки не лише міцності, а й загальної і місцевої стійкості та витривалості (у випадку повторних і динамічних навантажень). За другою групою граничних станів у сталезалізобетоні найчастіше перевіряють тріщиностійкість залізобетонної пли­ти та прогини балки. Головна мета розрахунку тріщиностійкості сталезалізобетонних балок по­лягає в забезпеченні належної їх довговічності (щоб уникнути корозії арматури плити). Причи­нами, які можуть зумовити появу тріщин, є спільна дія силових факторів і несприятливих впливів (наприклад, температури та зсідання бе­тону), зусилля попереднього напруження й ре­гулювання зусиль, від'ємні згинальні моменти в нерозрізних конструкціях тощо. У підручнику ці питання не розглядаються і для їх вирішення необхідно звертатися до спеціальної та норматив­ної літератури.

Обчислення прогинів сталебетонних балок від вертикальних навантажень виконують з ураху-

А б Рис. 11.8. Епюри нормативних різниць температур: а — для першого і другого варіантів; б — для третього варіанта.

Для конструкцій мостів обов'язковим є роз­рахунок динамічного прогину — амплітуди й час­тоти коливань. Наприклад, щоб уникнути резо­нансу, період вільних коливань у вертикальній площині для міських і пішохідних мостів не по­винен перебувати в інтервалі 0,45...0,60 с. Забез­печення горизонтальної жорсткості вимагає особ­ливої уваги для одноколійних залізничних ста­лезалізобетонних мостів. Період вільних горизон­тальних коливань не повинен перевищувати 0,01ї (де І — проліт, м), а також 1,5 с. Перше обме­ження обгрунтовано експериментальними даними про амплітуди вимушених горизонтальних коли­вань під дією рухомого залізничного навантажен­ня, друге — необхідністю уникнути резонансу з поривами вітру. Для міських і пішохідних мостів цей період не повинен перебувати в інтервалі 0,9...1,2 с.

Ash Перший Другий Третій варіант варіант варіант

Esh ь Рис. 11.9. Принципові епюри внутрішніх напружень і деформацій: а — від зсідання бетону плити (епюри деформацій); б — від змін температури для першого, другого і третього варіантів відповідно (епюри напружень).

Ванням змін у значеннях модуля деформування бетону, зумовлених тривалим навантаженням (див. рекомендації для a^et)- Окрім цього, стале - залізобетонні конструкції доволі часто мають ще й змінний переріз. Для розрізних балок, що пере­бувають під дією розподіленого (чи близького до нього) навантаження, прогин посередині прольоту можна визначити за спрощеною формулою

J — ^ . ^гпах ' f 1 + ^ • ^Ef.Sup (117)

48 EJet у 25 hi, sup j'

Де Mmax — найбільший згинальний момент посе­редині прольоту, lef, mi fef, sup — зведені до сталі моменти інерції перерізів відповідно посередині та на опорі балки.