Оптимизация условий обработки определяется знанием физических и тех­нико-экономических зависимостей, су­ществующих в данной области. Посколь­ку в настоящее время трудно учесть все зависимости, связывающие отдельные факторы, проявляющиеся в процессе обработки, на практике применяют частичную оптимизацию: используют только некоторые оптимальные факторы, при этом значения остальных факторов предполагаются.

Существуют три основные разновид­ности частичной оптимизации условий обработки:

1) однокритериальная, когда во вни­мание принимают минимальную единич­ную стоимость;

2) двухкритериальная, когда во вни­мание принимают минимальную единич­ную стоимость и необходимую шеро­ховатость поверхности;

3) трехкритериальная, когда во вни­мание принимают минимальную единич­ную стоимость, необходимую шерохо­ватость поверхности и необходимую точ­ность размеров.

Кроме этих разновидностей приме­няют и Другие разновидности методов оптимизации [5, 58, 66, 76].

Основной оптимизации условий обра­ботки, которая обычно выполняется с по­мощью ЭВМ, являются установленные технические ограниченияв виде уравнений. В общем случае при обра­ботке резанием требуются следующие зависимости-ограничения.

Ограничение 1. Связь между стой­костью инструмента, его конфигурацией и материалом режущей части, глубиной резания, подачей, механическими свой­ствами обрабатываемого материала, с одной стороны, и максимально возмож­ной скоростью резания, с другой сто­роны, определяется формулой

C„Dz°Ka

Или, если принять во внимание, что V = = nrfn/1000,

Nsy° = 3L8Cvdz°~>Kv (Tmf°Zn°Br°)-X,

(6.15)

Где V — скорость резания, м/мин; Cv — Коэффициент скорости резания, характе­ризующий нормативные условия работы; D — диаметр обрабатываемой поверхно­сти или диаметр инструмента, мм; kv — суммарный поправочный коэффициент на скорость резания, учитывающий раз­ницу с нормативными условиями обра­ботки; Т — стойкость инструмента, мин; T — глубина резания, мм; s — подача (мм/об, мм/зуб; мм/двойной шаг; мм/мин); 2 — число режущих кромок; В — ширина резания, мм; п — частота вращения, об/мин; m — показатель сте­пени стойкости инструмента; х„, уи, zv, nv, rv — показатели степени соответственно глубины резания, подачи, диаметра ин­струмента, числа режущих кромок, ширины резания.

Зависимость (6.15) показывает, что частота вращения п и подача 5 для за­данных условий (стойкости инструмен­та, материала и т. д.) не должны пре­вышать значений, определяемых нера­венством Nsy°^.B |, где В |—правая часть общей зависимости (6.15).

В целях отыскания линейных зави­симостей, необходимых для решения задачи с помощью линейного програм­мирования, логарифмируют функции, определяющие ограничения. Обозначим: In n = jci; In (100s) =X2 nB=-b. Тогда уравнение, определяющее первое ограни­чение, будет иметь вид

Ограничение 2. Связь между мощ­ностью резания Ne и мощностью глав­ного привода станка Nz выражается формулой

N,*^N2t). (6.16)

Эта зависимость также может быть выражена [58] уравнением ограниче­ния, имеющим следующий вид:

Пгх 1 -+- угхг ^ Ь 2.

Ограничение 3. Расчетная скорость резания, подача и заданная производи­тельность станка связаны уравнением - ограничением

X] +*2>6з.

Ограничение 4. Это ограничение устанавливает связь между расчетной скоростью вращения при резании и наи­меньшей частотой вращения исходя из кинематики станка. Естественно, что расчетная частота вращения шпинделя « = яРасч не должна быть меньше мини­мальной частоты «CTmin, определяемой кинематикой станка. Так как 1п« = Х|, a in нстmir] = 64, то уравнение-ограниче­ние имеет вид

XI Ь4.

Ограничение 5. Расчетная и макси­мально допустимая скорости резания связаны зависимостью (с технологиче­ской точки зрения это ограничение услов­ное) :

Xi^Bs.

Ограничение 6. Установление связи между расчетной частотой вращения при резании и максимальной частотой вращения исходя из кинематики станка дает уравнение

Х, < Ьа,

Т. е. прасч < Яст тах.

Ограничение 7. Расчетные скорость резания V и подача S, допускаемые по условиям прочности инструмента, свя­заны уравнением

Прх, +T/P*2< Ь7.

Ограничение 8. Связь между расчет­ными величинами V и s, допускаемыми по условиям жесткости инструмента, вы­ражается уравнением

N,X--YzX2^B%.

Ограничение 9. Расчетные парамет­ры и, s и точность обработки, допускае­мая жесткостью обрабатываемой дета­ли и способом ее крепления, связаны зависимостью

П, Х] Ьч.

Ограничение 10. Связь между расчет­ными значениями V и S, допускаемыми по условиям прочности механизмов стан­ка, определяется уравнением

TtsX] +I/SX2< 6 ю.

Ограничение 11. Связь между рас­четной подачей s и наименьшей подачей sCTmjn, допускаемой кинематикой станка, может быть получена из неравенства

S sct mirr

Где 6i, = lnsCTmin.

Ограничение 12. Связь между расчет­ной подачей и максимальной подачей sCTmax, допускаемой кинематикой станка, устанавливается зависимостью s^sCTmax, т. е.

Хг <612.

Ограничение 13. Связь между рас­четной подачей и подачей, допускаемой из условия получения заданной шеро­ховатости поверхности, определяется

Зависимостью s^.u-yRzr/25, где Rz— допустимая (заданная) шероховатость; г — радиус закругления вершины режу­щей кромки инструмента. Следователь­но, уравнение ограничения имеет вид

В результате составления всех нера­венств получается математическая мо­дель процесса резания металла на ме­таллообрабатывающем станке. В этой модели записанные вместе неравенства

Определяют систему А, характеризую­щую основные ограничения обработки.

Для модели требуется установить функцию Цели.

Для рассматриваемой модели эту функцию можно записать в виде

F Ц = х|**2 = тах

В результате следующего рассуждения. При соблюдении предусмотренной эко­номической стойкости инструмента па­раметры обработки оптимальны, Когда
время обработки наименьшее, а объем удаляемого металла (A = usi) наиболь­ший. Так как время обработки обратно пропорционально произведению подачи „и скорости резания (или частоты вра­щения), то время обработки минималь­но, когда произведение Sv (или Sn) мак­симально. А следовательно, при задан­ной глубине резания будет удаляться наибольший объем металла.

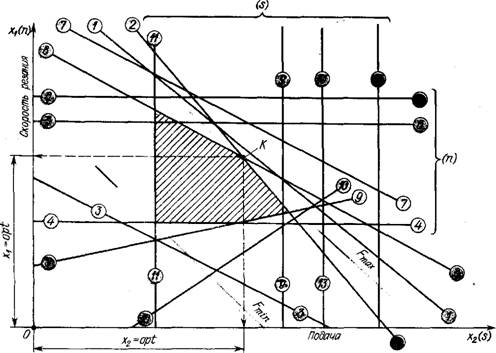
В геометрической интерпретации при­нятой математической модели (рис. 6.17) заштрихованное поле определяет мно­жество параметров обработки, допускае­мых ограничениями, принятыми в моде­ли. В..этом поле наиболее удаленная от начала системы точка К соответствует оптимальным значениям х, и х?..

Анализ математической модели про­цесса резания и метода определения оптимальных значений частоты враще­ния и подачи дает возможность разра­ботать универсальную програм­му [58] для расчета параметров режимов резания на токарных станках, имеющих предельное число дискретных частот вращения и подач. Программа позволяет выбирать оптимальные пара­метры резания с учетом всех ограниче­ний, наиболее существенных с точки зрения технологии изготовления и проч­ности обрабатываемой детали. Для того чтобы пользоваться этой программой, необходимы следующие входные данные [58]:

Рис. 6.17. Геометрическая интерпретация математической модели обработки при использовании Линейного программирования: / —13 — прямые, соответствующие уравнениям ограничений 1 —13

Rms — род обрабатываемого материала

D

It "

(сталь, чугун); Rma— род материала инструмента (твер­дый сплав, быстрорежущая сталь); Rm — прочность материала, МПа; НВ — твердость материала, МПа; Sm — марка (сорт) стали; D — наружный (внутренний) диа­метр обрабатываемого материа­ла, мм; L — длина точения, мм;

Квалитет точности IT;

H — шероховатость Ra, мкм;

T — глубина резания, мм; Smm — состояние материала; Ф — угол резания в плане, рад;

NN — номинальная мощность станка, кВт;

Я — множество подач станка; £2 — множество частот вращения шпин­деля. Xij - Выходные данные: Хг,- п — скорректированные частоты вра - ло­щения, подобранные в множест - х^ - ве Й, об/мин; x5j ■ S — скорректированные подачи, вы­бранные из множества л, мм/об; хщ TmOo—машинное время (по таблице),

Мин; xjj

Tm — машинное время, мин, рассчитан­ное по формуле Tm = fmlooXO. Ol L Xgj - Или Tm = L/(Ns), при этом вторую формулу применяют, когда значе­ние подач и частот вращения, подобранные из таблиц, не соот­ветствуют диапазонам подач и частот вращения, которыми рас­полагает токарный станок; тип режущей части; передний угол у, рад; ширина тела резца; высота тела резца; ширина тела резца, не регламен­тированная стандартом; высота тела резца, не регламен­тированная стандартом; радиус закругления режущей кром­ки г, мм;

■ параметр охлаждения.