Optical mode density in a one-dimensional resonator
 4 апреля, 2014
4 апреля, 2014  admin
admin In this section, the enhancement of spontaneous emission will be calculated based on the changes of the optical mode density in a one-dimensional (1D) resonator, i. e. a coplanar Fabry-Perot microcavity. We first discuss the basic physics causing the changes of the spontaneous emission from an optically active medium located inside a microcavity and then derive analytical formulas for the spectral and integrated emission enhancement. The spontaneous radiative transition rate in an optically active, homogeneous medium is given by (see, for example, Yariv, 1982)
|
(14.7) |
Wspont Tspont J о Wspont p(v l) dv l
where Wspont(l) is the spontaneous transition rate into the optical mode l and p(vl) is the optical mode density. Assuming that the optical medium is homogeneous, the spontaneous emission lifetime, xspont, is the inverse of the spontaneous emission rate. However, if the optical mode density in the device depends on the spatial direction, as in the case of a cavity structure, then the emission rate given in Eq. (14.7) depends on the direction. Equation (14.7) can be applied to some small range of solid angle along a certain direction, for example the direction perpendicular to the reflectors of a Fabry-Perot cavity. Thus, Eq. (14.7) can be used to calculate the emission rate along a specific direction, in particular the optical axis of a cavity.
The spontaneous emission rate into the optical mode l, Wspont(1), contains the dipole matrix element of the two electronic states involved in the transition (Yariv, 1982). Thus Wspont(1) will not be changed by placing the optically active medium inside an optical cavity. However, the optical mode density, p(v), is strongly modified by the cavity. Next, the changes in optical mode density will be used to calculate the changes in spontaneous emission rate.
We first compare the optical mode density in free space with the optical mode density in a microcavity. For simplicity, we restrict our considerations to the one-dimensional case, i. e. to the case of a coplanar Fabry-Perot microcavity. Furthermore, we restrict our considerations to the emission along the optical axis of the cavity.
|
|
|
2 n |
|
(14.8) |
|
p1D(v) = |
|
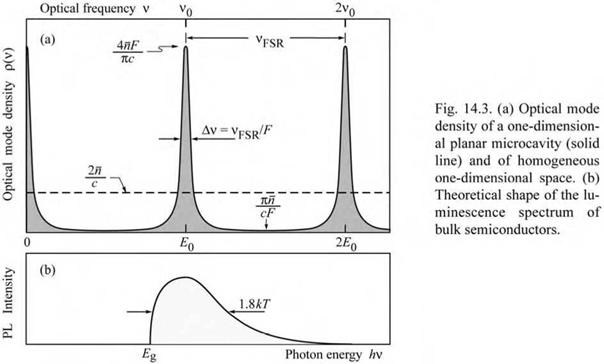
c where n is the refractive index of the medium. Equation (14.8) can be derived using a similar formalism commonly used for the derivation of the mode density in free space. The constant optical mode density given by Eq. (14.8) is shown in Fig. 14.3 (a). |
In a one-dimensional homogeneous medium, the density of optical modes per unit length per unit frequency is given by
Exercise: Optical mode density. Derive Eq. (14.8), i. e. optical mode density in a 1D space.
In planar microcavities, the optical modes are discrete and the frequencies of these modes are integer multiples of the fundamental mode frequency. The optical mode density of a planar microcavity is shown schematically in Fig. 14.3 (a). The fundamental and first excited mode
occur at frequencies of v0 and 2v0, respectively. For a cavity with two metallic reflectors (no
distributed Bragg reflectors) and a n phase shift of the optical wave upon reflection, the fundamental frequency is given by v0 = c/(2 nLcav), where c is the velocity of light in vacuum and Lcav is the length of the cavity. In a resonant microcavity, the emission frequency of an
optically active medium located inside the cavity equals the frequency of one of the cavity
modes.
The optical mode density along the cavity axis can be derived using the relation between the mode density in the cavity and the optical transmittance through the cavity, T(v),
p(v) = K T(v) (14.9)
where K is a constant. The value of this constant will be determined by a normalization
condition, i. e. by considering a single optical mode. Using Eq. (14.1), the transmission through a Fabry-Perot cavity can be written as
T T2
T (v) = ---------------------------------------------------------------- . (14.10)
1 + R2 - 2-yJRi R2 cos(4n n Lcavv / c)
The transmittance has maxima at v = 0, v0, 2 v0 ... , and minima at v = v0/2, 3 v0/2, 5 v0/2 ... .
The lorentzian approximation of a transmittance maximum at v = 0 is obtained by expanding the
cosine term in Eq. (14.10) into a power series using cos x « 1 - (x2 / 2), so that
T(v) = T1T2 (/W )-Vc)-2 . (14,1)
(l-УЦДГ ) + V2
(r1 R2 ) 1(4nnLcav/c)2 Integrating p(v) over all frequencies and the cavity length yields a single optical mode, i. e.
K JLc f* p(v) dv dL = 1 . (14.12)
J 0 J —*
The lower and upper limit of the frequency integration can be chosen to be ± да since the lorentzian approximation of Eq. (14.11) has only one maximum at v = 0. Using Eqs. (14.9),
P да 2 2 —1
(14.11), and the integration formula I (a + x ) dx = n/a yields
J —да
K = WR2/74 (1 — JRR). (14.13)
T1T2 c
|
|
Using Eq. (14.9), the optical mode density of a one-dimensional cavity for emission along the cavity axis is then given by
(14.14)
Equation (14.14) allows one to calculate the density of optical modes at the maxima and minima. At the maxima, the mode density is given by
p max = ^31 ^ . (14.15)
|
c |
1 — V R1R2
Using (R1R2)34 * 1 and the expression derived for the finesse F (see Eq. 14.4), one obtains an approximate expression for the mode density at the maxima
4 nF л 1
Pmax *------------------------ • (14.16)
n c
That is, the mode density at the maxima is proportional to the finesse of the cavity. At the minima, the mode density is given by
pmin = (R1 R.2)3'^^/)pr) . (14.17)
(1+VRRT )2 c
Using (R1R2)3 4 * 1 and the expression derived for the finesse F (see Eq. 14.4), one obtains an approximate expression for the mode density at the minima
n
Pmin * n F ■ (14.18)
cF
That is, the mode density at the minima is inversely proportional to the finesse of the cavity.
The comparison of the optical mode densities of a one-dimensional (1D) free space and a 1D planar cavity is shown in Fig. 14.3. Note that the mode density is conserved, i. e. the areas below the 1D mode density and the 1D cavity mode density are the same.


 Опубликовано в
Опубликовано в