Обработка экспериментальных данных
 19 декабря, 2013
19 декабря, 2013  admin
admin На практике при изучении диэлектрической релаксации полимеров определяют температурно-частотные зависимости компонентов комплексной диэлектрической проницаемости. При этом в соответствии с принципом температурно-временной эквивалентности (ТВЭ) можно проводить измерения в режиме изменения температуры с малой по сравнению с изменением т скоростью при фиксированной частоте внешнего электрического поля (скорость изменения температуры образца меньше 19 К/мин). В другом случае фиксируется температура образца и меняется частота внешнего электрического поля. Этот случай экспериментально осуществить труднее, так как требуется аппаратура, охватывающая широкий диапазон частот. Однако он открывает возможность строгого расчета некоторых параметров, характеризующих релаксационный процесс: полного поглощения (е0—Soo) или параметра распределения времен релаксации а. При непрерывном изменении температуры такая возможность уже отсутствует из-за наличия температурной зависимости а, поэтому получаемые кривые удается интерпретировать только качественно.
Обычно при обработке экспериментальных результатов подобных измерений получают зависимости е(со) и е"(со) при различ-
|
|
|
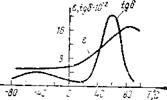
Рис. 7.5. Зависимость диэлектрических потерь tg б и проницаемости е от температуры для по - лиметилвинилкетона на частоте 103 Гц |
ных температурах. Как известно, увеличение температуры приводит в этом случае к смещению максимума е" по шкале частот. При этом кривая 8"=g" (со) проходит через максимум при условии
“max*— ИЛИ ^тах*—1. (7.13)
где vmax — частота, Гц, при которой диэлектрические потери максимальны. Влияние температуры на время релаксации достаточно хорошо описывается уравнением типа (7.4). Если воспользоваться полулогарифмическими координатами (lg т; Т~1)9 такая зависимость будет линейной при условии, что U—const. Это условие достаточно точно выполняется для локальных процессов. Действительно, из (7.4) следует lgt = lgTo+ [//(2,3/?Г), или с учетом выражения (7.13)
lg Vmax = lg — -------- • (7.14)
s m х s 2тсх0 2,3RT
Экстраполируя прямую (7.14) на T = оо (т. е. 1/7"=0), получаем значение постоянной то, а тангенс угла наклона прямой позволяет оценить энергию активации U.

 Опубликовано в
Опубликовано в