Обобщение экспериментальных данных исследования скорости движения разряда в плазмотронах в критериальной форме
 12 августа, 2016
12 августа, 2016  admin
admin При тех же предположениях, что были приняты при выводе критериальных зависимостей для характеристик дугового разряда, безразмерная скорость вращения должна быть функцией трех определяющих критериев, а именно:
Имеет смысл, однако, рассмотреть вопрос о допустимости одночленной степенной аппроксимации, имея в виду следующее. В плазмотронах диапазон изменения безразмерного определяющего параметра
относительно узок, поскольку его малые значения соответствуют низким термическим КПД, тогда как верхнее значение параметра
ограничивается двумя факторами: предельным значением, при котором еще обеспечивается режим устойчивого горения разряда, и минимальной магнитной индукцией, обеспечивающей потребную скорость перемещения разряда по электродам. В результате рабочий диапазон из-
—4 -6
менения параметра составляет 10 ...10 .
Ответ на вопрос о возможности одночленной аппроксимации при таком диапазоне изменения параметра может быть получен из анализа экспериментальных данных.
In *л/Ъ
 19мШ7П
19мШ7П
0
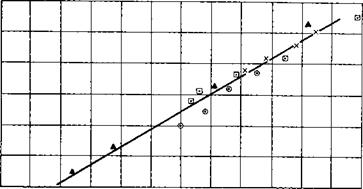
На рис. 8.28 представлены результаты экспериментов, приведенные в табл. 8.2, в виде зависимости
что соответствует размерной форме зависимости (8.23).
Оказывается, что такая зависимость может с достаточной степенью точности описать результаты экспериментов лишь в узком диапазоне изменения критерия П^, поскольку получаемые из выражения (8.27)
зависимости скорости вращения от различных параметров расходятся с истинными (особенно зависимости от плотности и магнитной индукции).
Анализ экспериментальных данных приводит к выводу, что это расхождение связано с неучетом влияния числа Рейнольдса на безразмерную скорость вращения. Этот вывод подтверждает рис. 8.29, где данные табл. 8.2 представлены в форме
V /V д О
![]()
![]()
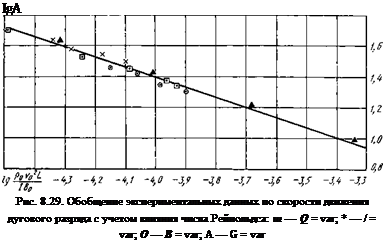 |
А08/ і/ X Ф (PQVQl/H0)
Видно, что формула (8.28) позволяет правильно описать влияние отдельных параметров (силы тока, магнитной индукции, давления, условной скорости обдува разряда рабочим телом) на скорость вращения и значительно уменьшить отклонение экспериментальных данных от результата, полученного по аппроксимирующей формуле, которая в этом случае в безразмерном виде приводится к следующей:

 Опубликовано в
Опубликовано в