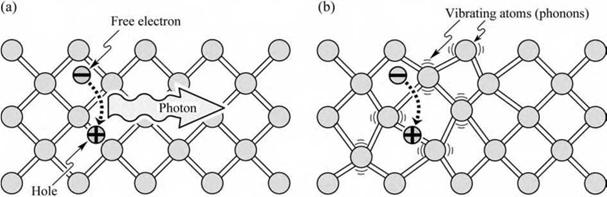
There are two basic recombination mechanisms in semiconductors, namely radiative recombination and non-radiative recombination. In a radiative recombination event, one photon with energy equal to the bandgap energy of the semiconductor is emitted, as illustrated in Fig. 2.5. During non-radiative recombination, the electron energy is converted to vibrational energy of lattice atoms, i. e. phonons. Thus, the electron energy is converted to heat. For obvious reasons, non-radiative recombination events are unwanted in light-emitting devices.

Fig. 2.5. (a) Radiative recombination of an electron-hole pair accompanied by the emission of a photon with energy hv ~ Eg. (b) In non-radiative recombination events, the energy released during the electron-hole recombination is converted to phonons (adapted from Shockley, 1950).

There are several physical mechanisms by which non-radiative recombination can occur. Defects in the crystal structure are the most common cause for non-radiative recombination. These defects include unwanted foreign atoms, native defects, dislocations, and any complexes of defects, foreign atoms, or dislocations. In compound semiconductors, native defects include interstitials, vacancies, and antisite defects (Longini and Greene, 1956; Baraff and Schluter,

1985). All such defects have energy level structures that are different from substitutional semiconductor atoms. It is quite common for such defects to form one or several energy levels within the forbidden gap of the semiconductor.

Energy levels within the gap of the semiconductor are efficient recombination centers; in particular, if the energy level is close to the middle of the gap. The recombination of carriers via a trap level is shown schematically in Fig. 2.6. Owing to the promotion of non-radiative processes, such deep levels or traps are called luminescence killers.

і

© ее

Fig. 2.6. Band diagram illustrating recombina­tion: (a) non-radiative via deep level, (b) non- radiative via Auger pro­cess and (c) radiative.

	Tnon-rad	Tnon-rad		Trad
			1 1
	* E'y	Photon '
6	в 6	&e 6	в e	В

(a)

(b)

(C)

*Fi

The recombination of free carriers via deep levels was first analyzed by Shockley, Read, and Hall (Hall, 1952; Shockley and Read, 1952). The non-radiative recombination rate through a deep level with trap energy ET and concentration NT is given by (Shockley and Read, 1952)

(2.23)

P0 А n + щ A p + A n A p

RSR ="

(NT vp ° p) 1(n0 + n1 + An) + (NT vn ° n) 1(P0 + Pi + AP)

where An = Ap; vn and vp are the electron and hole thermal velocities, and an and ap are the capture cross sections of the traps. The quantities n1 and p1 are the electron and hole concentrations if the Fermi energy is located at the trap level. These quantities are given by

n1 = niexp ^ Et kE j and P = niexp ^ EFlkTET j (224)

where EFi is the Fermi level in the intrinsic semiconductor.

The non-radiative lifetime of excess electrons can be deduced from the equation Rsr = An/т. Consequently, the lifetime is given by

p0 + "0 + A" (2.25)

1

T (NT vp °p) 1("0 + "1 + А") + (NT vn °n) 1(p0 + pi + bp)

We now differentiate between majority carriers and minority carriers and assume that the semiconductor is p-type. Then holes are in the majority, i. e. p0 >> n0 and p0 >> p1. If we further assume a small deviation from equilibrium, i. e. An <<p0, then the minority carrier lifetime is given by

— = = NT vn о n. (226)

T T"0

If electrons were the majority carriers, the lifetime would be obtained in an analogous way, i. e.

11

= NT vp °p. (2 27)

T T P0

The results show that the Shockley-Read recombination rate is limited by the rate of capture of minority carriers. This result suggests itself since the capture of majority carriers is a much more likely event than the capture of minority carriers. Equation (2.25) can then be written as

(2.28)

1 = p0 + "0 + А"

T

Tp0 ("0 + "1 + А") + Tn0 (0 + p1 + АРу '

For small deviations from equilibrium, i. e. An << p0, the equation simplifies to

T = ТщАШ - + Tp0 "0 + "1 +A" - . (2.29)

0 p0 + "0 p0 + "0 0 p0 + "0

Inspection of the equation reveals that the lifetime does not change for small deviations from equilibrium in an extrinsic semiconductor.

(2.30)

For further insight, we assume that the trap captures electrons and holes at the same rate, i. e. vna„ = vpap and Tno = xpo. One obtains from Eq. (2.29)

T T"0

v P0 + "0 j

For the special case of intrinsic material, i. e. n0 = p0 = ni, the equation simplifies to

P1 + "1

Et — E

Fi

(2.31)

1 +

Ti

= T"

0

0

kT

2 n

ij

1 + cosh

where EFi is the intrinsic Fermi level, which is typically close to the middle of the gap. The cosh function has a minimum when the argument of the function is zero. Thus the non-radiative lifetime is minimized if ET - EFi is zero; i. e. when the trap level is at or close to the midgap energy. For such midgap levels, the lifetime is given by т = 2 xno. This result demonstrates that deep levels are effective recombination centers if they are near the middle of the gap.

Inspection of Eq. (2.31) also reveals the temperature dependence of Shockley-Read recombination. As T increases the non-radiative recombination lifetime decreases. As a result, the radiative band-to-band recombination efficiency decreases at high temperatures. The highest band-to-band radiative efficiencies of direct-gap semiconductors can be obtained at cryogenic temperatures.

However, some devices are based on radiative recombination through a deep state. A well- known example of radiative recombination mediated by a deep level is N-doped GaP. It follows from the Shockley-Read model that the deep-level recombination rate increases with increasing temperature.

In indirect-gap semiconductors such as GaP, radiative transitions are mediated by phonons. That is, radiative recombination must be accompanied by absorption or emission of a phonon. Since phonons are more abundant at high temperatures, radiative recombination (mediated by the absorption of a phonon) can increase with temperature.

In the vicinity of a deep level, the luminescence intensity decreases. A single point defect will be difficult to observe due to its relatively small effect. Frequently, however, defects group into clusters of defects or extended defects. Such extended defects are, for example, threading dislocations and misfit dislocations occurring when epitaxial semiconductors are grown on mismatched substrates, i. e. substrates with a different lattice constant from that of the epitaxial layer. There are also many other types of extended defects. The luminescence-killing nature of extended defects is illustrated in Fig. 2.7, which shows a cathodoluminescence micrograph of a GaAs layer measured at room temperature. The figure reveals several dark spots. Luminescence in the vicinity of the defects is reduced due to the non-radiative recombination channels so that the defects manifest themselves as dark spots. The size of the dark spots depends on the size of the defect and the minority carrier diffusion length.

While most deep-level transitions are non-radiative, some deep-level transitions are radiative.

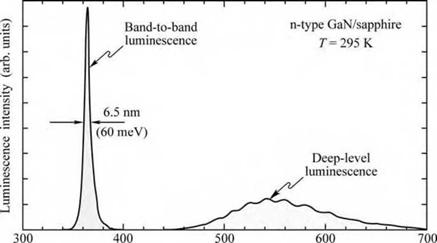
An example of a radiative deep-level transition in GaN is shown in Fig. 2.8 (Grieshaber et al., 1996). The luminescence spectrum shows the band-to-band transition at 365 nm and a broad deep-level transition around 550 nm. The deep-level transition occurs near the yellow range of the visible spectrum. The yellow luminescence line has been shown to be due to Ga vacancies (Neugebauer and Van de Walle, 1996; Schubert et al. 1997; Saarinen et al. 1997), a common point defect in n-type GaN.

Fig. 2.7. Cathodoluminescence micro­graph of a GaAs epitaxial layer. The dark spots are due to large clusters of non-radiative recombination centers (after Schubert, 1995).

GaAs И—И

T = 295 К 10 pm

Deep levels can be caused by native defects (group-III vacancies, group-V vacancies, group- III interstitials, and group-V interstitials), unwanted foreign impurities, dislocations, impurity - defect complexes, and combinations of different types of defects. Frequently it takes many years to unambiguously identify the atomic nature of a defect. For a review of defects in semiconductors see, for example, Pantelides (1992).

Fig. 2.8. Room-tempera - ture photoluminescence spectrum of GaN with a band-to-band optical transition at 365 nm and a second transition at 550 nm identified as an optically active deep - level transition (after Grieshaber et al., 1996).

Wavelength X (nm)

Another important non-radiative recombination mechanism is Auger recombination. In this process, the energy becoming available through electron-hole recombination (approximately Eg), is dissipated by the excitation of a free electron high into the conduction band, or by a hole deeply excited into the valence band. The processes are shown schematically in Fig. 2.6 (b). The highly excited carriers will subsequently lose energy by multiple phonon emission until they are close to the band edge.

The recombination rates due to the two Auger processes shown in Fig. 2.6 (b) are given by

RAuger = Cpnp (2.32)

and

RAuger = Cnn p. (2.33)

Auger recombination is proportional to the square of the carrier concentration (either p2 or n2) since two carriers of the same type (either two holes or two electrons) are required for the recombination process. The first process (see Eq. 2.32) is more likely to happen in p-type semiconductors due to the abundance of holes. The second process (see Eq. 2.33) is more likely in n-type semiconductors due to the abundance of electrons.

During Auger recombination, energy and momentum must be conserved. Owing to the

differences in conduction and valence band structure in semiconductors, the two Auger

coefficients Cp and Cn are generally different.

In the high-excitation limit in which the non-equilibrium carriers have a higher concentration than equilibrium carriers, the Auger rate equations reduce to

RAuger = (Cp + Cn) n3 = Cn3 (2.34)

where C is the Auger coefficient. The numerical values of Auger recombination can be determined by a quantum mechanical calculation that takes into account the band structure of the semiconductor (see, for example, Agrawal and Dutta, 1986). Typical values for the Auger coefficient are 10-28-10-29 cm6/s for III-V semiconductors (see, for example, Olshansky et al., 1984; Agrawal and Dutta, 1986).

Auger recombination reduces the luminescence efficiency in semiconductors only at very high excitation intensity or at very high carrier injection currents. This is due to the cubic carrier concentration dependence. At lower carrier concentrations, the Auger recombination rate is very small and can be neglected for practical purposes.

2.3 Non-radiative recombination at surfaces Substantial non-radiative recombination can occur at semiconductor surfaces. Surfaces are a strong perturbation of the periodicity of a crystal lattice. Recall that the band diagram model is based on the strict periodicity of a lattice. Since this periodicity ends at a surface, the band diagram will need to be modified at a semiconductor surface. This modification includes the addition of electronic states within the forbidden gap of the semiconductor.

Next, we consider a semiconductor surface from a chemical point of view. Atoms at the surface cannot have the same bonding structure as bulk atoms due to the lack of neighboring atoms. Thus some of the valence orbitals do not form a chemical bond. These partially filled electron orbitals, or dangling bonds, are electronic states that can be located in the forbidden gap of the semiconductor where they act as recombination centers. Depending on the charge state of these valence orbitals, the states can be acceptor-like or donor-like states.

The dangling bonds may also rearrange themselves and form bonds between neighboring atoms in the same surface plane. This surface reconstruction can lead to a locally new atomic structure with state energies different from bulk atomic states. The surface bonding structure depends on the specific nature of the semiconductor surface. The energetic location of surface states is very difficult to predict, even with powerful theoretical models. Thus phenomenological models of surface recombination are commonly used.

It has been shown that electronic states within the forbidden gap appear at semiconductor surfaces. Bardeen and Shockley (Shockley, 1950) pioneered the understanding of surface states and their role as recombination centers.

Next, we calculate the effect of surface recombination on the carrier distribution in a p-type semiconductor subjected to illumination. Assume that the illumination causes a uniform steady - state generation rate G. The one-dimensional continuity equation must be fulfilled at any point in the semiconductor. The continuity equation for electrons is given by

5A"(xt) = G - R + 1A Jn (2.35)

dt e dx

where Jn is the current density caused by electrons flowing to the surface. In the bulk of the uniform semiconductor, there is no dependence on space and thus the continuity equation reduces to G = R under steady-state conditions. Using the recombination rate in the bulk as given by Eq. (2.14), the excess carrier concentration in the bulk is given by An„ = G Tn as indicated in Fig. 2.9. Assuming that the electron current is a diffusion current of the form

(2.36)

Jn = eDn

dAn( x, t) д x

and inserting the diffusion current into Eq. (2.35) yields the continuity equation for diffusive currents, i. e.

(2.37)

dt

n

2 дАn(x, t) An(x, t) d An(x, t) ----------------- = G----------------------------- +- Dn —

д x

Surface

(a)

Fig. 2.9. (a) Illuminated p-type semiconductor, (b) band diagram, and (c) minority and major­ity carrier concentra­tions near the surface assuming uniform car­rier generation due to illumination. The ex­cess carrier concentra­tions are An and Дp.

p-type semiconductor

• • A	» 4	I
1/ —Surface states I
ОООООО ооооо с	3

(b)

к		f— P = P0 + 4p(*) = P0
J—s=0		f— n = n0 + An(.x)
--- Low	1 surface recom - 1 bination velocity	t An0 = Gzn . .*_______________ I...
= 0		X

(с) о

c У

с о

0 0 - U 00 о

At the semiconductor surface, carriers will recombine rapidly due to surface states. The boundary condition at the surface is given by

дА n( x, t) д x

(2.38)

eDn

x = 0

x = 0

= eS Аn(x, t) =

where S is the surface recombination velocity. The boundary condition states that minority carriers diffusing to the surface will recombine at the surface. We assume that the generation rate

is constant with time, and thus the minority carrier concentration has no time dependence. The steady-state solution to the differential equation with the above boundary condition is given by

Tn S exp (-x / Ln) Ln + TnS

1 -

(2.39)

n(x) = no + An(x) = no + An0

The carrier concentration near a semiconductor surface is shown in Fig. 2.9 for different surface recombination velocities. For S ^ 0, the minority carrier concentration at the surface is identical to the bulk value, i. e. n(0) ^ n0 + Anro. For S ^ ro, the minority carrier concentration at the surface approaches the equilibrium value, i. e. n(0) ^ n0.

Surface recombination leads to a reduced luminescence efficiency and also to heating of the surface due to non-radiative recombination at the surface. Both effects are unwanted in electroluminescent devices. The surface recombination velocities for several semiconductors are summarized in Table 2.1. The data shown in the table show that GaAs has a particularly high surface recombination velocity.

Table 2.1. Surface recombination velocities of several semiconductors (GaN data after Tu et al., 2000; Aleksiejunas et al., 2003). Semiconductor Surface recombination velocity GaAs S = 106 cm/s GaN S = 5 x 104 cm/s InP S = 103 cm/s Si S = 101 cm/s

Experimental evidence of surface recombination is illustrated in Fig. 2.10, which shows the luminescence emanating from a stripe-like current-injection contact on a GaAs laser chip. The luminescence is viewed from the substrate side so that the stripe-like metal contact is “behind” the light-emitting region. Figure 2.10 clearly reveals that the luminescence decreases in the near­surface region.

Surface recombination can occur only when both types of carriers are present. It is important in the design of LEDs that the carrier-injected active region, in which naturally both types of carriers are present, be far removed from any surface. This can be achieved, for example, by carrier injection under a contact that is much smaller than the semiconductor die. Furthermore, the contact must be sufficiently far away from the side surfaces of the die. If the current flow is confined to the region below the contact, carriers will not “see” any semiconductor surfaces.

Note that unipolar regions of a semiconductor device, e. g. the confinement regions, are not affected by surface recombination due to the lack of minority carriers.

Several passivation techniques have been developed to reduce the surface recombination in semiconductors, including treatments with sulfur, and other chemicals (Lipsanen et al., 1999).

Fig. 2.10. (a) Micrograph and (b) schematic frontal view of a GalnAs/GaAs structure with a stripe-shaped top contact and contact window on substrate side under current injection conditions. The luminescence emanating from active region located below the stripe clearly decreases in the vicinity of the surface due to surface recombination.