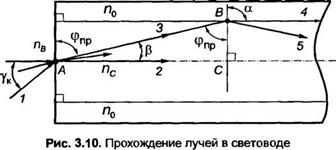
Направим световой пучок на торец СВ как показано на рис. 3.10. Пучок ограничен двумя крайними лучами / и 2. Луч 1 составляет угол ук с осью симметрии СВ, луч 2 распространя­ется вдоль оси симметрии СВ.

Луч / преломляется на границе пв -» «с под углом Р и превращается в луч 3. Соответст­вующая лучу 3 волна в точке В распадается на две: волна 4 преломляется в среду с АПП = п0 под углом а, волна 5 отражается от границы пс ->• п0.

Назовем угол ук — критическим и потребуем, чтобы ему соответствовал предельный угол падения ф = cp„p на границу раздела пв -> по (рис. 3.10). Тогда угол преломления а = п/2 и волна 4 скользят вдоль границы раздела пс -> щ. В окрестности точки А закон преломле­ния света имеет вид: пв siny* = пс sin Р, где пв — АПП среды, из которой свет попадает на торец СВ. Из треугольника ABC имеем Р = п/2 — ф„р; sinp = со5фпр. Следовательно,

Пв sin у„ = nr cos ф ; cos ф = — sin у„.

Пс

В окрестности точки В

>VsintPrp =nDsm^nQ sinфпр — w0*

Возводя во вторую степень (3.12) и (3.13) и складывая нх почленно, имеем

| —I sin2 YK + “y = 1; «fiSin2yK =nl-nl nB sinyK - nl = A.

NcJ «с

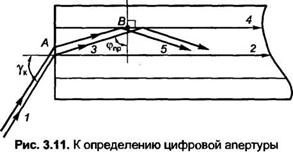Выражение (3.14) носит назва­ние нормальной числовой апертуры стекловолокна. Согласно рис. 3.10 и 3.11 при у<ук в окрестности точки В имеет место ПВО, и свет распро­страняется вдоль СВ по зигзагооб­разной траектории. При у > ук усло­вие ПВО не выполняется, и энергия волны 3 постепенно переводится в оболочку.