НЕСТАЦИОНАРНЫЙ ТЕПЛОВОЙ ПОТОК. Температуропроводность и общий закон теплопроводности
 11 мая, 2013
11 мая, 2013  admin
admin Тепловой поток, проходящий через тело, изменится в том случае, если изменится температурное поле в рассматриваемом теле. Предположим, например, что температура правой поверхности стенки (см. рис. 1) под действием внешнего нагревания внезапно поднимется до более высокого значения, например до температуры /2. Тогда ранее установившийся процесс теплоотдачи наружу прекратится и тепло пойдет в противоположном направлении, к стенке. Следовательно, в этом случае в стенку тепло будет передаваться с обеих сторон и полностью аккумулироваться, вызывая повышение температуры стенки. С повышением температуры внутри стенки тепловой поток ослабевает. Наконец, когда все температуры примут свои определенные значения, на-
Ступит новое установившееся состояние с соответственно уменьшенной теплоотдачей. Напротив, тепло отдавалось бы стенкой I* обе стороны, если бы произошло внезапное понижение темпера* туры t. В этом случае иступила бы деаккумуляция тепла, накопленного стенкой. Когда /ке температура не будет более изменяться, наступит новое установившееся состояние. Из этих примеров ясна физическая причина, которая приводит к нарушению установившегося состояния и к временному последствию этого нарушения. Этой причиной является изменение теплосодержания тела в связи с изменением температурного поля. Часть поступающего тепла будет идти на повышение теплосодержания тела, и, наоборот, если теплосодержание тела уменьшается вследствие понижения температуры, то произойдет усиление теплового потокам Часто температура наружной поверхности тела изменяется неоднократно, например испытывает периодические колебания (в регенераторах); в этом случае тепловой поток никогда не будет постоянным и распределение температуры внутри тела покажет периодически колеблющееся изменение во времени и пространстве.
Физическим свойством, которое влияет на эти процессы, явля* ется не теплопроводность, а температуропроводность.
Она объясняется следующим образом; Повышение температуры распространяется от слоя к слою и требует в соответствии с предыдущими рассуждениями затраты тепла на аккумуляцию. Определенное количество тепла Q сообщает рассматриваемому телу тем более высокую температуру, чем меньше удельная теплоемкость материала соб (ккал/мгград). Эта зависимость является линейной (определение удельной теплоемкости). Следовательно, интенсивность распространения температуры, мерой которой является коэффициент температуропроводности а, должна быть обратно пропорциональна удельной теплоемкости
Q
Единицы объема ст. е. а = — , где С — коэффициент пропор-
^об
Циональности. Скорость распространения температуры тем выше, чем быстрее поднимается температура в соседнем слое. Этот подъем пропорционален количеству поступающего тепла. Прй данной разности температур это количество тепла, согласно закону Фурье, пропорционально величине теплопроводности X; следовательно, температуропроводность должна выражаться уравнением а = С'* —, где С' — новый коэффициент пропорциональное
Ности, который зависит лишь от выбранной системы измерения. Мы принимаем его для постоянно применяющейся здесь технической системы мер (м; час; кг) равным единице. Удельная теплоемкость единицы объема известна:
|
(53) |
![]() Соб = с Т ккал/м*град,
Соб = с Т ккал/м*град,
Где с — удельная теплоемкость единицы веса, ккал/кг • град-, Т ■—удельный вес материала, кг/м3.
Отсюда коэффициент температуропроводности
Необходимо подчеркнуть, что вышеуказанное 'определение температуропроводности физически не вполне обоснованно, но оно
Правильно отражает факторы, от,/ которых зависит скорость распро-
« странения температуры в изменяю
Щемся во времени температурном поле. Сообразно с этим температура растет быстрее всего в телах, в которых высокая теплопроводность сочетается с малой удельной теплоемкостью единицы объема.
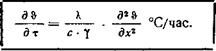 Изменение температуры в стен-' ке от координаты х и времени т (при. условии, что тепло распространяется лишь в направлении оси *) выражается следующим дифференциальным уравнением второго порядка в частных производных, ко-т торое выводится из общего закона теплопроводности Фурье
Изменение температуры в стен-' ке от координаты х и времени т (при. условии, что тепло распространяется лишь в направлении оси *) выражается следующим дифференциальным уравнением второго порядка в частных производных, ко-т торое выводится из общего закона теплопроводности Фурье
Здесь и в дальнейших рассуждениях этого раздела через 0°С обозначаем переменную температуру и через т — время.
Вывод, Рассмотрим (процессы, протекающие в бесконечно малом объеме йУ*=йх*йу. йг (рис. 4). Так как предполагается, ^то изменяющийся тепловой поток распространяется лишь в направлении оси х, то в этот объем поступает количество тепла и выходит фг- Поэтому внутри объема остается:
На левой поверхности рассматриваемого объема (х = х) наблюдается пере' д §
Пад температуры —г— °С/м. Тогда по уравнению (2) количество тепла, по - дх
Ступающего в объем за время (1%, будет равно
ДЪ. *
О. = X • Аи • йг • —— • й т ккал. дх
ПЕРЕДАЧА ТЕПЛА ТЕПЛОПРОВОДНОСТЬЮ 53
------ >„! -— --------------------------------------------------------------------------------------
Температурный перепад = л, согласно предположению, изменяется во
Времени и. пространстве. Пространственное изменение в направлении оси х дк
Выразится через ——, если предположить, что температурный перепад
Ох
Уменьшается с увеличением х (т. е. при +йх получается —сВД. Таким об-
Разом, на участке йх это изменение составит — —г— йх или, если подста-
Ах
, д* дЧ ; ^ вить Н = то—ах. Это является изменением температурного перепада на пути от х до х + йх. Поэтому температурный перепад на расстоя-
Нии х + йх равен т— — _ — йх. В соответствии с этим количество тепла,
Дх дх2
Выходящее из рассматриваемого объема за ®ремя йх, составит но уравнению (2)
/ дЬ
|
<58) |
Следовательно, количество тепла, остающееся в объеме в соответствии с уравнениями (57) и (58), будет равно
Д2&
(? = (?1 — 02 = * ' &У Аг • й т • йх. (59)
Этому количеству тепла соответствует определенное повышение температуры &Ъ в объеме. Температурное изменение в объеме за единицу времени
Аа а»
Составит - ^ " °С, следовательно, за время йх оно будет равно.^т°С, Количество тепла, соответствующее этому изменению температуры, равно
ДЬ
О = с-^йх-йу-йг —— й х о т
TOC o "1-5" h z или после подстановки ф из уравнения (50) 1
ДЧ д 8
Л*йх йу-йг й т = с-ц йХ'йу >йг ~—йг;
Отсюда находим искомое уравнение (55)
X дЧ д&
с • 7 дх2 а т
Применение частного дифференциала д означает, что на главную переменную Ф одновременно влияют две независимые друг ог друга переменные, а именно х и х однако частная производная позволяет рассматривать эту зависимость лишь от одной независимой переменной, в то врейя как предполагается, что другая переменная — временно постоянная величина. На-
А 8
Пример, —— означает повышение температуры О с течением времени х> при-
О X
Чем текущая координата (х) принята постоянной величиной. В задачах технической физики в качестве независимых переменных почти исключительно встречаются пространство и время. Поскольку пространство и время одновременно влияют на какой-нибудь процесс, он может быть описан только дифференциальным уравнением в частных производных. Обычно можно исхо-
Дйть из предположения, сделанного в приведенном выше выводе, что тепловой поток распространяйся в направлении оси х. Если же тепловые потоки наблюдаются и в направлении осей у и г, то пользуясь почти теми же рассуждениям«, суммируют количество тепла, остающееся в объеме по направлению осей х% у иг, получая общее количество тепла, идущее на повышение температуры в рассматриваемом объеме.

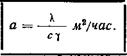
 Опубликовано в
Опубликовано в