Рассмотрим процесс распространения тепла в неограниченном теле с нулевой начальной температурой от непрерывно действующего точечного источника тепла постоянной мощности .

Элемент тепла от точечного источника тепла, вспыхнувшего в момент времени за время T- вызовет к моменту времени T Приращение температуры [8]

(4.21)

Температуру найдем, интегрируя (4.21)

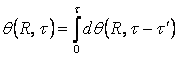(4.22)

Н. Н. Рыкалиным [8] показано, что интеграл (4.22) приводится к виду:

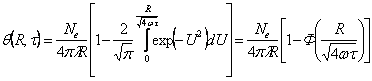, (4.23)

Где – известный интеграл вероятности Гаусса, значения которого могут быть найдены по таблицам или вычислены численными методами.

Н. Н. Рыкалиным [8] для установившегося температурного режима (т. е. при T ® ¥) получено решение для температуры полубесконечного тела от точечного источника мощностью , движущегося по его поверхности:

, где (4.24)

В частности, для неподвижного (т. е. при V = 0) непрерывно действующего точечного источника постоянной мощности q при длительном нагреве (T ® ¥) температура полубесконечного тела стремится к предельному стационарному состоянию и зависит только от радиуса R, плотности теплового потока q и коэффициента теплопроводности L [8]:

. (4.25)

Это решение может быть применено, например, для оценки предельного температурного поля в массивной плите (полубесконечном теле) при коротком замыкании сварочной цепи.

Пусть ток короткого замыкания равен 250 А, а напряжение 1 В. При этом мощность источника тепла, который условно будем считать точечным, равна 250 Вт. Коэффициент теплопроводности медной плиты равен 360 , а стальной – 40 . Распределения температуры в зависимости от расстояния от источника тепла для этих условий показано на рис. 4.19.

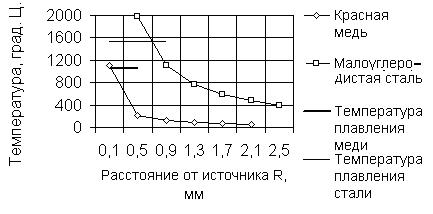
Рис. 4.19. Зависимости температуры от расстояния точки

От точечного источника тепла мощностью 250 Вт, непрерывно

Действующего на поверхности полуограниченного тела

Согласно решению (4.24) температуры на поверхности полуограниченного тела в направлении движения точечного источника за источником тепла (отрицательная полуось X<0) и перед источником (положительная полуось X>0) будут различными.

Для отрицательной полуоси X<0 зависимость температуры от расстояния R рассматриваемой точки от точечного источника вытекает из уравнения (4.24) при X=–R .Эта зависимость точно такая же, как и для неподвижного источника тепла (4.25) [8]:

(при X<0). (4.26)

При X>0, X=R Из уравнения (4.24) следует [8]:

(при X>0). (4.27)

Из (4.27) следует, что чем больше скорость V Движения источника тепла, тем быстрее убывает температура впереди источника (рис. 4.20).

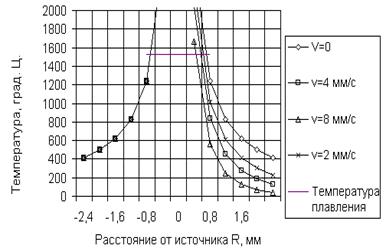
Рис. 4.20. Влияние скорости перемещения точечного источника на распределение температуры предельного состояния по оси X В полубесконечном теле: =250 Вт, l= 40 ,

W= 0,000008

Полагая в уравнении (4.24) X=0 , получим распределение температур по оси OY, т. е. в направлении, перпендикулярном направлению движения источника [8]:

. (4.28)

Сопоставление формул (4.26), (4.27) и (4.28) показывает, что в боковом направлении температура убывает медленнее, чем перед источником в направлении его движения, но быстрее, чем за источником.

Отвод тепла из зоны шва в стороны от средней линии вносит соответствующие изменения в температурное поле, в связи с чем изотермы будут иметь вид, показанный на рис. 4.21 [12].

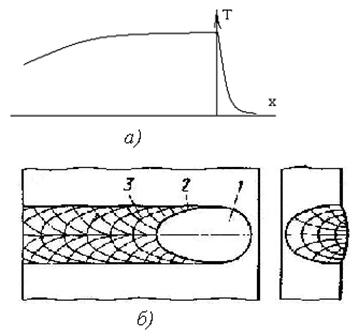
Рис. 4.21. Схема распределения температуры в сварном шве, изотермических линий и траекторий тепловых потоков:

1– сварочная ванна, 2 – изотермы, 3 – столбчатые кристаллиты

Вследствие такого распределения изотерм и линий тепловых потоков кристаллизация металла в сварном шве будет происходить путем образования криволинейных столбчатых кристаллов с линией симметрии по оси сварного шва.

Для ряда технологических задач сварки представляет определенный практический интерес и ранее рассмотренное решение (2.35) о распределении температуры в полуплоскости от быстродвижущегося равномерно распределенного источника тепла (рис.4.22) [1]:

. (4.29)

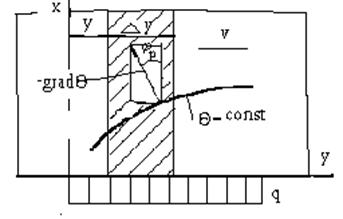
Рис. 4.22. Схема к расчету температуры в полуплоскости

От быстродвижущегося равномерно распределенного

Источника тепла

Как следует из (4.29), при постоянной плотности теплового потока Qф увеличение скорости V источника тепла приводит к уменьшению температуры, возникающей на поверхностях свариваемых деталей. Следовательно, для выдерживания постоянного (рационального) уровня температуры при увеличении мощности источника сварочной дуги необходимо соответственно увеличивать скорость перемещения электрода.