Уравнение предельного состояния процесса распространения тепла при нагреве пластины подвижным линейным источником постоянной мощности, перемещающимся со скоростью V при , согласно методу точечных источников тепла, может быть записано в виде (рис. 4.22) [8]:

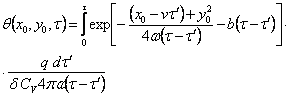. (4.30)

Здесь – коэффициент, учитывающий интенсивность понижения пластины при теплоотдаче в окружающую среду в , a – коэффициент теплоотдачи (рис. 4.23).

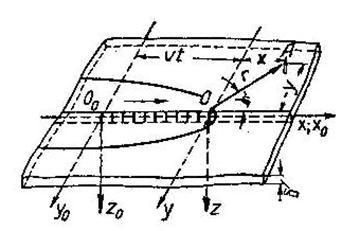
Рис. 4.23. Схема замены непрерывно действующего

Движущегося в пластине источника тепла совокупностью

Элементарных мгновенных источников

Интеграл (4.30) приводится к виду [8] :

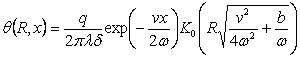. (4.31)

Значения этой функции могут быть определены по таблицам [8]

Или графикам (рис. 4.24).

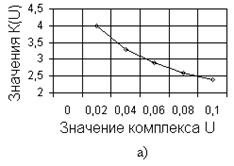
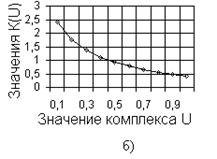
Рис. 4.24. Функция

Значения функции могут быть также определены, вычисляя численными методами интеграл вида [8]:

.

Для неподвижного источника уравнение (4.11) при V=0 примет вид [8]:

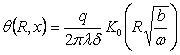. (4.32)

В пластине тепло распространяется в двух направлениях, и тепловой поток больше стеснен, чем в полубесконечном теле с трехмерным распространением тепла. Поэтому с удалением от источника температура в пластине (кривая 2) убывает медленнее, чем в полубесконечном теле (кривая 1) (рис. 4.25).

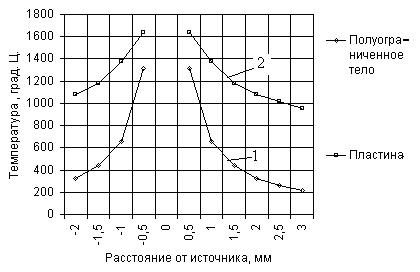
Рис. 4.25. Зависимость температуры от непрерывно

Действующего источника в стальном полуограниченном теле

И в стальной пластине, Q=330 Вт

Качественно зависимость температуры от мощности источника, от теплофизических характеристик, расстояния от источника, теплофизических характеристик материала пластины остается такой же, как и для полубесконечной плиты.