7.6.1. Постановка задачи

При разработке линейной теории дуги переменного тока был сделан целый ряд допущений. Некоторые из них не вызывают особых возраже­ний (например, цилиндрическая симметрия, неучет приэлектродных процессов в длинной дуге), в то время как другие являются весьма

грубыми. В данном разделе учтем существенно нелинейные зависимости р(Л) и а(Л) (нелинейная теория). Учет конвекции, т. е. радиального движения газа, обусловленного изменением плотности газа по радиусу и во времени, значительно усложняет расчет, так как в этом случае пришлось бы решать полную систему нелинейных уравнений газовой динамики. Поэтому, как и ранее, пренебрежем соответствующим кон­вективным членом в уравнении энергии, а затем, вычислив изменение профиля энтальпии по радиусу и по времени, оценим величину кон­вективного переноса теплоты по сравнению с молекулярной тепло­проводностью.

Рассмотрим следующие вопросы.

1. Насколько сильно влияет нелинейный характер зависимостей р(Л) и а(Л) на результаты расчета дуги переменного тока?

2. Как меняется во времени профиль энтальпии и соответственно некоторая условная зона проводимости (условный радиус дуги)?

3. Согласуются ли между собой результаты расчетов по линейной и нелинейной теориям?

Для ответов на эти вопросы необязательно задавать точный вид зависимости р(Л), поскольку речь идет, в первую очередь, о ка­чественных результатах. Поэтому запишем уравнение состояния газа в

виде р = р[( 1 - 1 /к)Л] 1 и примем 1-1 /к = const, т. е. при р =

= const р - Л *. Такая аппроксимация р(Л) позволяет существенно уменьшить время численного расчета.

Перейдем теперь к зависимости а(Л). Анализ показал, что для различных газов она хорошо аппроксимируется следующим выражением:

о = (a^h + а°)[1 - ехр(- а2Л7)],

давления. В этой формуле первый сомножитель отражает почти линейную зависимость а от Л при высоких энтальпиях, а второй сомножитель отражает сильный рост о при малых энтальпиях. Приведенная формула позволяет аппроксимировать реальные расчетные или экспериментальные кривые o(h) с точностью не хуже 5 %.

Излучение дуги не учитывается. Остальные допущения те же, что и в линейной теории. Рассматривается наиболее простая элек­трическая цепь, в которой последовательно с дугой включена индук­тивность.

Уравнения энергии, цепи и закон Ома в безразмерной форме имеют вид

аЛ/Эт * * Л(Э2Л/Эг2) + (k h/r)bh/br + k i2a h f a Tdr] ;

1 1 2 1 0 J

dt/Эг = sin(r + ip) - ik S a rdr ; (7.20)

13 0 }

it = ilk f a rdr

1 3 0 J

Здесь приняты следующие обозначения:

h = Л/Л° = а, Л/о°: и - и/е ; і = їх./е ;

I ш L т

k{ = (1 - l/K)a°kh(a{pur20fl;

k2 = (1 - lK)(em/xL)2(djt2pcM°r4Qfl;

k = 2яг2о°лґ. .

З 0 L

Краевые условия

Л(і. г) = о. (эл/э7)г=о = 0.

Ш, о) = Hr), 7(0) = о.

т. е. рассматривается процесс установления периодического режима горения дуги.

Система уравнений (7.20) является интегро-дифференциальной. Для ее численного решения используется конечно-разностный метод с

итерациями по Л и і на каждом шаге по времени. Заметим, что совместное решение требуется лишь для первых двух уравнений сис­темы (7.20), из которых определяются Л(г, т) и і(т), а затем из третьего уравнения определяется и(т).

Расчеты проводились для дуги, горящей в воздухе при атмосферном давлении. Выбраны следующие значения койстант: к = 1,2; а° = 1600 0м 1м!; Л° = 2,58-104кДж/кг; = 6,21 10 2Ом ^кг м! кДж *;

а2 = 0,088; 7 = 3,9; со = 341 1/с; k^ = 1,5-Ю^4 кг/м*с.

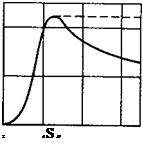
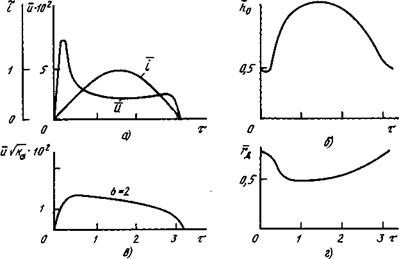
На рис. 7.11 приведены кривые и и і в установившемся режиме при

г = 1 см, і = е /х, = 10 А (е /I = 700 В/см; *.// = 70 Ом/см). о т т L т L

Кривая напряжения на дуге имеет значительный пик зажигания,

превосходящий напряжение в середине полупериода почти в 4 раза.

Форма кривой тока близка к синусоиде, так как при выбранных

параметрах ток в цепи в основном определяется индуктивным

сопротивлением (см. рис. 7.11, а). Аналогичные результаты при том

же Гф получены при значениях = 100 и 1А, хотя в последнем

случае пик зажигания меньше (и - 2) и более сглажен.

J т

Рис. 7.11. Напряжение, сила тока, энтальпия на оси и условный ра - диус дуги в функции времени: І = 10 А; Г = 1 см т 0

Таким образом, кривые напряжения весьма сильно отличаются от соответствующих кривых линейной теории. Попытаемся сблизить обе теории, для чего придадим результатам линейной теории новую интерпретацию. Напомним, что в расчетах по линейной теории мгновенное значение напряжения и относится к эффективному значению U, которое (без учета излучения) вычисляется по формуле

и = (и//г )(kjk ),/2. (7.21)

1 д по

По определению и по своему физическому смыслу эффективное напряжение U в установившемся режиме не зависит от времени. В нелинейной теории вычисленное по формуле (7.21) значение U нельзя рассматривать как эффективное напряжение дуги, так как оно не является постоянным, ввиду того что коэффициент зависит от

времени. Действительно, при линейной аппроксимации кривой o(h) необходимо знать ее рабочий участок, т. е. фактически знать значение энтальпии на оси ftQ. Только в этом случае можно с

достаточной точностью определить kg. Таким образом, между и kg

существует однозначная связь. Рассчитанная по методу минимального отклонения зависимость А^(Л) при давлении р = 0,1 МПа показана на

рис. 7.12. Видно, что k весьма сильно меняется, особенно в

о

диапазоне изменения Л от 0 до 2,5. Поскольку при горении дуги меняется Лф, соответственно меняется и kg. Поэтому в приведенном выражении U следует рассматривать как функцию времени U ~ —1 /2

[кд(т)] . Предположим, что в этом случае линейная теория дает

не истинную форму напряжения на дуге и(т), а некоторую функцию и ІЇГ = f{r). Это означает, что в каждый момент времени линейная теория дает такое значение и, которое получалось бы, если начиная с этого момента коэффициент kg оставался бы постоянным.

Теперь по результатам нелинейной теории перестроим зависимость

и(т) в зависимость и ІЇІГ от г, для чего воспользуемся зависимостью

Рис. 7.12. Зависимость коэффициента ли-

___ kff

нейной аппроксимации кривой О (А) от эн - ^
тальпии для воздуха при р * 0,1 МПа

энтальпии на оси AQ от времени г (см. 1

рис. 7.II, б). Процедура перестройки вы-
полняется следующим образом. Для каждого

- - г о

момента времени находим значения и и п^, затем по Aq определяем по кривой рис. 7.12 значение и находим и •Ї1Г. Полученная зависимость и от т представлена на рис. 7.П,

в. Эта кривая весьма похожа на кривые напряжения на дуге в ли­нейной теории. Проведенный расчет и сопоставление показали, что полученная кривая практически совпадает с кривой линейной теории при Ь = 2 и а > I. Это и последующие значения Ь были получены пу­тем подбора по наилучшему совпадению форм и. Аналогичные резуль­таты получены при і = 100 А (Ь = 4) и і = I А (b = I). тп ш

Можно сделать следующий вывод: в рассмотренных случаях линейная теория дает некоторое обобщенное напряжение на дуге и JaT, которое

существенно отличается от истинного напряжения и. Однако далее
будет показано, что при достаточно большой температуре на оси дуги

результаты расчетов и по обеим теориям совпадают.

Рассмотрим изменение радиуса дуги переменного тока. Разобьем весь канал на зону вблизи оси с большой электропроводностью (собственно дуга) и зону с малой электропроводностью (непроводящая зона). Границей между зонами служит окружность, где А = А^, а А^

определяется из условия a(Aj) = aa(AQ), где а « I (далее принято

а = 0,01). Очевидно, что определенный таким образом радиус дуги г

д

будет переменным во времени, так как зависит от т. На рис. 7.11, г показано изменение радиуса дуги в течение полупе - риода: г меняется приблизительно от 0,5 до 0,75, т. е. в среднем

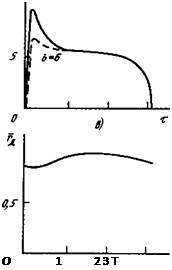
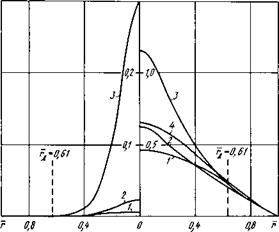
Рис. 7.13. Профили энтальпии и электропроводности в различные мо - менты времени: 1...4 соответствует Т * 0,04; 0,33; 1,40; 2,92

г » 0,63. Аналогичные результаты получены при = 100 и 1 А (г^

в обоих случаях также равен приблизительно 0,6).

Рассмотрим изменение энтальпии и электропроводности по радиусу

канала. На рис. 7.13 представлены профили а и Л для различных моментов времени при і = 10 А. Здесь же штриховой линией отмечен

средний условный радиус дуги. При г > г изменения энтальпии не-

д

велики и уменьшаются с увеличением г. Значение а слабо влияет на

значение г. Отметим еще следующее обстоятельство. Кривые 1 и 2, 3 д

и 4 на рис. 7.13 пересекаются между собой. Это следствие того, что термическая инерционность столба и отдельных его зон достаточно велика. Поэтому при нагреве столба дуги энтальпия газа вблизи оси увеличивается, а в периферийной области продолжает уменьшаться (кривые 1 и 2). При остывании наблюдается обратная картина (кривые

3 и 4). Следовательно, в данном случае профили Л(г) в разные мо­менты времени неподобны.

Q г)

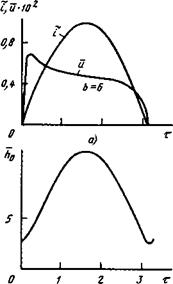
Рис. 7.14. Напряжение, сила тока, энтальпия на оси и условный ра-
диус дуги в функции времени:

І » 1000 А: г - I см т О

Переходим к рассмотрению результатов нелинейной теории при rQ = I см и і = 1000 А. Из рис. 7.14, а видно, что кривая и(т) прак­тически совпадает с аналогичной кривой, полученной при расчете по линейной теории при Ь = 6. В то же время кривая и {ІГ значительно отличается от нее в первой части полупериода (рис. 7.14, в). Это объясняется тем, что для пересчета и в и 4F при полученных зна­чениях Ло (рис. 7.14, б) используется падающий участок кривой МЛ) (см. рис. 7.12). Таким образом, вместо сглаживания, как было при і = 1...100 А, пик зажигания возрастает (рис. 7.14, в). От-

ЇЇІ

сюда следует, что при больших токах, когда энтальпия на оси в те­чение всего полупериода выше, чем энтальпия, соответствующая мак­симуму кривой МЛ), линейная теория дает истинную кривую н(т). На
рис. 7.14, г показано _изменение условного радиуса дуги по времени. Средний радиус дуги г ~ 0,85, т. е. несколько больше, чем в пре­дыдущих случаях. Аналогичные результаты получены при = 4,5 см, im = 1000 А: радиус дуги оказался равным 0,73 и практически не зависел от времени.

Итак, интерпретация результатов расчета напряжения по линейной теории существенно зависит от рабочего участка кривой МЛ). Для

того чтобы придать этим результатам единообразие, модернизируем кривую МЛ). Будем считать, что после достижения максимума (см.

рис. 7.12) k остается постоянным (штриховая линия на рис. 7.12).

Теперь можно сделать следующий обобщающий вывод: линейная теория

дает правильную форму обобщенного напряжения на дуге и ЇМ причем

эта форма совпадает с истинной, если рабочим участком универ­сальной кривой k^(h) является ее прямолинейный участок.

Расчеты показали, что если для вычисления V по линейной теории пользоваться формулой (7.21) (при = 0), причем к^ вычислять по

универсальной кривой МЛ) для средней за полупериод энтальпии на

оси (Лл ♦ Лл . )/2, то рассчитанные по линейной и нелинейной

0 max Omin

теориям мгновенные значения и хорошо согласуются между собой.

Ранее при сравнении линейной и нелинейной теорий параметр не­линейности b находили по форме кривой и путем соответствующего

подбора. Однако расчеты показали, что если в формулу (7.8) под­ставлять значение к, определенное по средней за полупериод эн­тальпии на оси, то расчетное значение Ь во всех рассмотренных случаях оказывается близким к найденному по кривой.

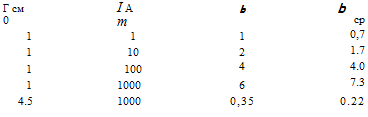Результаты всех рассчитанных вариантов приведены ниже.

Здесь значение параметра Ь определено по форме кривой, а значение Ь рассчитано по среднему за полупериод значению плотности газа на оси.

Результаты данного раздела позволяют сделать два основных вывода.

1. Если энтальпия газа в дуге достаточно велика и рабочей об­ластью кривой о(Н) является участок относительно слабого роста, учет нелинейной зависимости a(h) не приводит к каким-либо качест­венным изменениям по сравнению с линейной теорией; в противном случае, т. е. при малой энтальпии, наблюдаются существенные разли­чия результатов линейной и нелинейной теорий.

2. Учет нелинейной зависимости р(Л) вместо условия к = const

Р

не приводит к качественным изменениям по сравнению с линейной

теорией, о чем говорят, в первую очередь, результаты расчета при

г = 1 см, і = 1000 А.

0 т

С целью выяснения влияния допущения Х/с = = const на ре­

зультаты расчета эту величину варьировали. При изменении к^ъ 1,4 раза расчетные значения менялись не более чем на 3 %, т. е. указан­ное допущение можно считать обоснованным. Аналогичный вывод можно сделать и относительно допущения (1 - 1 /к) = const.

Как в линейной, так и в нелинейной теориях не учитывается кон­вективный перенос теплоты в радиальном направлении, обусловленный радиальной скоростью су, возникающей в канале без протока газа вследствие изменения плотности р во времени и по радиусу. Из уравнения (7.16) следует, что отношение членов, выражающих кон­вективный перенос теплоты и передачу теплоты за счет теплопровод­ности, равно pcyr/fcПоскольку нелинейная теория дает возможность

рассчитать р(г, /), то из уравнения неразрывности применительно к рассматриваемому случаю можно вычислить

рог = — Э^ / prdrj/Э/ и найти указанное отношение. Расчеты показали, что влияние кон­векции на передачу теплоты мало по сравнению с теплопроводностью.

Изложенные результаты показывают, что разработанная теория правильно описывает все особенности горения дуги переменного тока

в различных электрических цепях, такие, как пики зажигания, паузы тока, искровой характер разряда в цепи с емкостью и т. д. Она дает возможность рассчитывать переходные и установившиеся режимы в сложных цепях с дуговыми разрядами и на основании этих расчетов выбирать оптимальные значения параметров. В соответствии с теорией из реальных осциллограмм напряжения на дуге можно сделать ряд качественных выводов. Например, если на осциллограмме напряжения дуги постоянной длины имеются большие пики зажигания, то это го­ворит о низкой температуре газа в дуге. Если такие пики отсут­ствуют, то температура весьма высока.