Динамика электротепловых процессов при точечной сварке очень сложна. Достоверных теоретических расчетов по этой теме не создано до сих пор не только по причине их сложности. Всего вероятнее, главная причина заключается в том, что производство вполне обходится без этих расчетов, поскольку значительно легче и, самое главное, точнее установить оптимальный режим сварки непосредственно на практике и тем самым обойтись без тепловых расчетов. Однако, как уже отмечалось выше, расчетные системы, если они хорошо отображают реальную действительность, весьма необходимы для понимания физической сущности исследуемого процесса. Исходя из этого принципа, здесь и рассматриваются закономерности выделения теплоты при формировании расплав­ленного ядра сварной точки.

Независимо от того, с какой точностью предполагается опре­делять взаимосвязи всех переменных, которые управляют выде­лением теплоты в металле в результате прохождения тока, нельзя обойтись без понятий электрических сопротивлений самого металла и металлических контактов. В п. 1.4 уже обращалось внимание на тот факт, что электрические сопротивления самих сваривае­мых деталей как проводников электрического тока только в ред­ких случаях определяются их геометрическими размерами. Та­кой редкий случай имеет место для стыковой сварки цветных ме­таллов, когда можно пренебречь поверхностным эффектом и со­противление стыкуемых концов рассчитать по элементарной фор­муле

R = pl/S.

К сожалению, в некоторых даже современных литературных источниках эту элементарную формулу рекомендуют как достовер­ную для точечной сварки, вводя в формулу разные коэффициенты:

R = (pl/S) Аа.

Формулы такого рода теоретическая электротехника отвергает.

Как было показано в формуле (1.65), х — это не размер про­водника, а протяженность линий тока, пронизывающих провод­ник. Точно также S — это не геометрический размер какого-то сечения проводника, а площадь переменного сечения потока си­ловых линий электрического тока. Кривизна линий электриче-

Екого тока, их плотность в различных участках про­водящего элемента опреде­ляются, в первую очередь, не геометрией проводни­ка, а его физическими ха­рактеристиками в зоне про­хождения тока: магнит­

ной проницаемостью р, удельным сопротивлением р. Обе эти характеристики, каждая по-своему, зависят от температуры и общих магнитных или немагнит­ных свойств свариваемого металла.

При контактной точеч­ной сварке очень сложна не только конфигурация проводников, но также сложны и очень нестабильны во времени температур­ные поля в зоне свариваемых контактов.

С точки зрения вложения энергии в зону свариваемого кон­такта нас интересуют два главнейших фактора: программа изме­нения сварочного тока во времени и активные сопротивления, которые определяют ту энергию Джоуля, которая обеспечивает необходимую активацию свариваемого контакта. Для точечной сварки эта' активация должна заканчиваться плавлением ядра будущей сварной точки. В тексте, относящемся к рис. 1.25, уже предварительно было показано, что измерять мы можем только полное сопротивление контакта /?кт, равное для идеально чистых поверхностей

Rkt — Гмг 4* грт. (2.62)

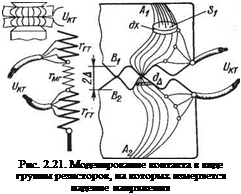
Раздельно измерить составляющие гмг и ггт нельзя. Этот факт иллюстрируется еще одной наглядной схемой измерения, приве­денной на рис. 2.21. Контакт двух микропирамид моделирован резистором гмг, а пучки линий электрического тока по металлу (участки А1 — Вх и А2 — В2) моделированы резисторами ггт. Здесь же показано, что измерительные проводники неизбежно снимают суммарную разность потенциалов: гмг и ггт.

Для двух единичных пирамид

где 5Д — площадь микропирамиды.

Сопротивление всех контактирующих микропирамид уже оп­ределялось по формуле (1.79). Сопротивление самого металла ггт, в общем виде обозначенное через R, определялось по формулам (2.23) и (2.25).

4 К. А. Кочергнн

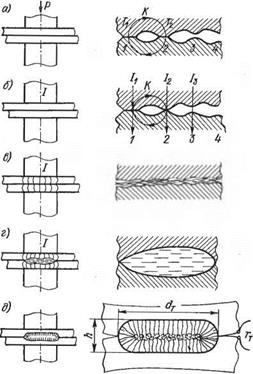
Рис. 2.22. Последователь­ность нагрева контакта при точечной сварке и формиро­вания ядра сварной точки (гт — электрическое сопро­тивление расплавленного ядра в момент выключения тока)

Как видно, значение гмг и лгт раздельно можно определить только расчетным путем. Таким образом, все предшествующие рассуждения об электрических сопротивлениях контактов и деталей полностью оправдывают смысл первой фразы этого пара­графа. Процессы выделения джоулевой теплоты в металле при формировании точечно-сварного соединения идут при изменяю­щихся сопротивлениях и при изменяющемся сварочном токе. Рассмотрим динамику этого процесса не только в общем виде, но и с учетом некоторых конкретных количественных характери­стик (рис. 2.22, а—д). Наиболее сложная картина выделения теп­лоты имеет место при сварке магнитных металлов и притом не самой малой толщины.

Прежде чем будет включен сварочный ток, ударом электро­дов создается механический контакт двух шероховатых поверх­ностей деталей (рис. 2.22, а). Этот первый эпизод контактирова­ния уже показывает приближенность расчета начального сопро­тивления контакта по формуле (1.79).

Действительно, эта формула определяет электрическое сопро­тивление или двух, или одной контактирующей пирамиды как сопротивление проходящему по ним сварочному току. Однако 98
тока в позиции рис. 2.22, а еще нет. Тем не менее в этом, пока еще только механическом контакте уже идут чисто электрические процессы. Удар, создав неравномерную деформацию в микрокон­тактах 1 и 2, тем самым вызвал сильную экзоэлектронную эмис­сию, которая в малой мере существовала и до того в этих выступах, так же как в точках 3, 4 и других, за счет операции подготовки поверхности как механическими средствами, так и химической обработкой. Неравенство температурных вспышек в точках 1 и 2 даст неравенство и термоэлектронного эффекта. В механическом контакте на рис. 2.22, а уже циркулируют замкнутые электротоки К, плотности которых могут быть и непредвиденно значительными.

Если сварочный ток включился (рис. 2.22, б), то элементарные токи /1У /2 могут алгебраически суммироваться-с круговыми то­ками и тем самым вносить свое дополнительное усложнение в расчетную формулу (1.79).

Остановимся еще некоторое время на первом мгновении вклю­чения тока и посмотрим, что должно происходить с сопротивле­нием контакта без учета замкнутых круговых токов.

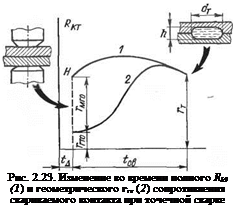
На рис. 2.23 воспроизведена типовая кривая изменения пол­ного сопротивления контакта RKT во времени, подобная той, что представлена на рис. 1.27, с той лишь разницей, что за пер­вое мгновение после включения тока длительностью tA изменение сопротивления пирамид не показано. Это первое мгновение пра­вильнее исследовать отдельно, с помощью нижеприведенных формул и рис. 2.24, а.

Изменение размеров микропирамиды во времени можно пред­ставить такими закономерностями:

	(2.63)
У = {/о + (й — Уо)	(2.64)

Температура единичных пирамид

ТА = Т0 (t/tA)n.

Показатели степеней р, ц, п могут быть различными, в зависимости от программы изменения давления электродов во времени. Удель­ное сопротивление микропирамид определяем по формуле

Рд = Ро [(1 + *Гд)] [ 1 + еСд/°т• (2.65)

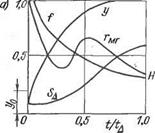
Учитывая соотношенияД2.63), (2.64), на рис. 2.24, а построены вероятные кривые изменения размеров микропирамид в Преде­лах времени длительностью /д. На основании формулы (1.76) построена кривая изменения сопротивления микропирамид, ко­торую мы приближенно определяем как электрическое сопро­тивление микрошероховато'го контакта гмг (рис. 2.24, а). Как 4* 99

Рнс. 2.24. Изменение электрического сопро-
тивления контактирующей пирамиды в про-
цессе ее нагрева и деформации в первые
мгновения после включения тока

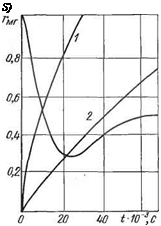видно, значение гмг в момент t — fat т. е. в точке Н, должно со­ответствовать этому же значению на рис. 2.23.

Представим, что сварочный ток через контакт нарастает по программе 1 или 2 (рис. 2.24, б). Из этого же рисунка видно, что квадрат тока по программе 1, умноженный на значение гмг, в мо­мент t — 10 мс даст эффект тепловыделения в шесть с лишним раз больше, чем ток по программе 2 в тот же момент времени. Такая интенсификация тепловыделения обязательно создает расплавлен­ный диск, но не обязательно одинаковой толщины. Может иметь место и резкий перегрев в какой-то зоне и, как следствие, вы­плеск жидкого металла из этой зоны. Если же программа тока была подобрана правильной, то вместо смятых микропирамид, осуществлявших контактирование, в плоскости свариваемого контакта создастся правильный круговой диск расплава.

Что же происходит с электрическим сопротивлением 2 (см. рис. 2.23). Для того чтобы выяснить, как изменяются все состав­ляющие сопротивления в зоне контакта, снова сделаем количе­ственное сравнение, используя те же данные для сварки стальных листов 4 + 4 мм, которые были приведены в п. 1.3. Удельное со­противление холодного металла р„ = 20 мкОм-м; расплавленного 100

р, ----- 140 мкОМ"М. При я/А = 25, а/ат = 14 000/25 000 рд = = 895 мкОм*м. При / = 35,35 мкм; X ~ 14 000/(85 000-2-І) = = 0,082

2 Дрт 2-60-140 3Ас ~ 3-0,57-104

Это сопротивление холодного контакта группы микропирамид. Но вот произошло их плавление и образовался расплавленный диск. Удельное сопротивление металла здесь стало рт == = 140 мкОм-м, а сопротивление самого диска

оказывается весьма малым. Вместе с тем, кривая показывает в момент £д сопротивление в десятки раз большее. Вот это и есть результат неотделимого от плоскости диска искривления линий электрического тока, пронизывающих расплавленный диск.

Если бы речь могла идти о статическом электрическом поле вокруг расплавленного диска, т. е. если не учитывать магнит­ного сжатия линий электрического тока, то сопротивление его прохождению оказывала бы составляющая

Ггто = РId. (2.66)

Формула эта, как и многие другие, известна из теории зазем­лений, где допускают возможным рассчитывать сопротивления по уравнению Лапласа, а ие Максвелла, т. е. не учитывать эф­фект сжатия линий тока магнитным потоком. В формуле (2.66) р — удельное сопротивление расплава; d — диаметр диска.

Формула (2.66) имеет в виду, что две полубесконечные массы металла контактируют друг с другом только через расплавлен­ный диск. Таким образом, линии тока, проходя из одной половины в другую и пронизывая диск, искривляются, что и фиксируется как добавочное к объемному электрическое сопротивление не только расчетом, но и измерением. Полагая, что в первое мгно­вение расплавленный диск окружен холодным металлом и его удельное сопротивление соответствует именно такому значению температуры, по формуле (2.66) находим

гГто — 20/1,2 = 17 мкОм.

Этот результат следует считать для случая магнитного металла, вероятно, заниженным. Магнитный поток сожмет силовые линии тока и они примут вид скорее такой, как схематически показано по сечению нижнего листа на рис. 1.25, чем такой, как в верхнем листе того же рисунка.

Определим более достоверную форму области протекания тока, используя формулы (2.16), (2.17), (2.23) и (2.25).

Примем силу сварочного тока / = 10 000 А. При d0 = 0,85 см Я = 3746 А/см. По кривой намагничивания (см. рис. 2.2) находим р-=. 5. Тогда по формуле (2.16)

6ЭКВ = 5000 У 20-106/(5-50) = 1,44 см;

Расчет показал, что б данном случае размер b меньше d0, и, следо­вательно, линии тока в металле сжаты, как это показано в ниж­нем листе рис. 1.25.

Все эти численные результаты не следует считать полностью достоверными. Расчеты проделаны для того, чтобы показать, ка­кого уровня могут быть отдельные составляющие электрических сопротивлений в зоне свариваемого контакта и в нем самом. Расчеты показывают, в том числе, совершенную нестабильность начального сопротивления мйкро - и макрогеометрии линий про­текания электрического тока, т. е. нестабильность полного со­противления свариваемого контакта. Как видно, эту нестабиль­ность нельзя устранить какими-либо регулирующими устройст­вами, нельзя и ориентироваться на нее при расчетах.

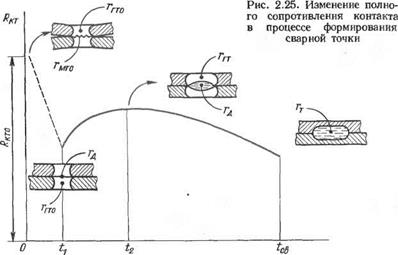
Расчетные примеры, показанные выше, можно подытожить посредством наглядного графика, приведенного на рис. 2.25. Здесь показана временная зависимость полного сопротивления контакта и на ней отмечены отдельные характерные эпизоды изменяющихся сопротивлений, поясняемые табл. 2.1. Наиболь - 102

шая неопределенность относится к начальному интервалу вре­мени: от t = 0 до t = h-

Наибольшая стабильность характерна для момента выключе­ния тока, т. е. для готового, расплавленного ядра сварной точки с заданными его размерами dT и h. В таком случае для сварки идеально чистого металла, когда роль тонких, оптически прозрач­ных оксидных пленок несущественна, для формулы (1.39) можно написать

qt = 4/2pTfc/(nd?), (2.67)

соответственно этому температура в плоскости контакта

Т = /2pTft V t

15 m Vкус ж/тблгі| ’

где принято S = JidT6.

Формула (2.68) имеет вспомогательный характер и только показывает взаимосвязь переменных процесса выделения теплоты в приближении не изменяющегося за время сварки действую­щего значения сварочного тока.

Картину выделения теплоты в контакте для импульсных режимов сварки металлических поверхностей, покрытых оксид­ной пленкой, следует рассмотреть отдельно. Задача эта очень сложная, и ее решение под силу только ЭВМ. Что же касается производственников-технологов, то им необходимы такие расчет­ные соотношения, которые правильно ориентируют понимание взаимосвязей всех переменных, участвующих в процессе. Исходя из этих условий, построим расчетную схему на целом ряде до­пущений и упрощений.

Примем допущение, что при импульсных режимах точечной сварки все энерговыделение в зоне свариваемого контакта идет на плавление ядра цилиндрической формы диаметром dT и вы­сотой h. Форму кривых сварочных токов будем учитывать по формулам (2,44) и (2.45). Полное сопротивление свариваемого контакта с учетом оксидной пленки на нем определим суммой

Rki — гМР + ггт + гпл» (2.69)

тогда тепловой баланс запишется равенством

(їі -)-1! (U2) (гш + ггт + гпп) = ycS^hdB. (2.70)

Первый сомножитель развернем по формулам (2.44) и (2.45). Вторым сомножителем займемся отдельно — в нем все слагаемые в процессе сварки переменны. Учтем только те характеристики, которые меняются в наибольшей степени. Для слагаемого ггт это будет удельное сопротивление металла вокруг контакта. Вместо общепринятого его значения рт — р0 (1 + ссТ) примем более краткую зависимость удельного сопротивления от абсо­лютной температуры 6. Тогда для многих металлов можно запи­сать зависимость

Р = РтЄ/Єші, (2.71)

где р. г — удельное сопротивление в момент плавления.

Учитывая (2.71), примем размеры ядра неизменяющимися, и для этого условия геометрическая составляющая сопротивле­ния контакта обозначится так:

р h pTh Є

гт ~ ST “ sT еп„ *

Электрические сопротивления микропирамид шероховатости по формулам (1.79), (1.80) в расчет вводить невозможно, иначе решение уравнения (2.70) окажется доступным только ЭВМ. Мы же ставим задачу получить возможно большую наглядность взаимозависимостей переменных параметров. Приведенный выше численный пример показал, что гмг0 от начального значения, весьма 104
значительного, уже при малых значениях критерия X переходит в новое качество — в расплавленный диск. Примем изменение гмг по упрощенной зависимости

rw - - ф- (1 - X). (2.73)

От

Здесь критерий X, по аналогии с критерием Z [см формулу (1.7)1, запишем в таком виде:

X ------- Ра0/ог0пя. (2.74)

Коэффициент р определяет характер обработки контактирующих поверхностей металла (см. табл. 5 приложения):

Р - ЄплДЄхол (1 - т - 2) Ь].

Значительно сложнее дело обстоит с составляющей гпл элек­трического сопротивления оксидной пленки. Для условий кон­тактной точечной сварки эта величина практически является неопределенной переменной. Существующие литературные источ­ники дают некоторые характеристики оксидов, но, к сожалению, измеренные в статическом состоянии и при определенной техно­логии изготовления оксида. Ничего подобного при точечной сварке нет. Электрические характеристики пленок на свариваемом ме­талле неопределенны и зависят от структуры размеров и времени существования пленок с момента зачистки. Этот последний фак­тор определяет интенсивность экзоэлектронной эмиссии и, следо­вательно, косвенно влияет на удельное сопротивление пленки. Для оксидных пленок в условиях точечной сварки большинства металлов (кроме алюминия и его сплавов) можно уверенно счи­тать только одну зависимость достоверной — это уменьшение удельного сопротивления с увеличением температуры. Мало того, можно считать, что при плавлении металла оксидные пленки растворяются в расплаве, и тогда их сопротивление вообще можно не учитывать. Исходя из такого рода соображений, примем

где 6 — удельное сопротивление оксидной пленки; ф — ее тол­щина.

Подставляя теперь в равенство (2.70) все его отдельные слагае­мые и сомножители в развернутом виде, получим довольно гро­моздкое уравнение:

Не менее громоздким получается и решение этого уравнения даже с использованием упрощений

Є =

^ jexp [-g-(P,/,

сгт

РдД + ЕФ

В этой формуле роль каждой переменной процесса просматри­вается с трудом, поэтому из нее будем устанавливать некоторые конкретные взаимосвязи, способные подсказать методы техноло­гического регулирования процесса сварки. Прежде всего рас­кроем значение временной функции F (/). Для принятых степен­ных функций (2.44) и (2.45)

В зависимости от кривизны эпюры нарастающего тока F (/) та­ково:

п................................... 4 2 1 1/2 1/4 1/10

F(t)................... . . 0,11т 0,2т 0,33т 0,5т 0,66т 0,83т

Вот эта. формула для технолога представляет непосредствен­ный практический интерес. Она показывает, что для любого размера ядра скорость нарастания его температуры сильнейшим образом зависит от начального сопротивления шероховатостей и оксидных пленок на них, т. е. от величин гмг0 и гпл0.. Поскольку нельзя эти переменные уменьшить, то все решается формой кри­вой тока, т. е. числом п (см. рис. 2.12). Как видно, более тонкое регулирование температуры в плоскости контакта достигается 106

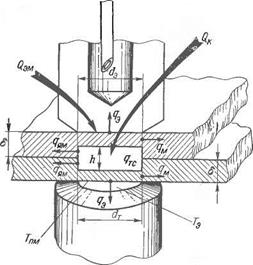
Рис. 2.26. Схема тепловых потоков при точечной сварке

именно путем изменения числа п, а не плотности сварочного тока. Как уже было показано, начальное сопротивление холодного контакта, определяемое в том числе величиной гмг, зависит от критерия X [см. формулы (1.13) и (1.14)]. Стоит заметить, что коэф­фициент Ь, характеризующий обработку контактирующих по­верхностей (см. табл. 5 приложения), может меняться от 1 до 8 при самых обычных способах подготовки металла под сварку. Что же касается изменения отношения действующего давления к пределу текучести р/от, то это число в реальных условиях мо­жет быть изменено только в пределах 0,2—0,5. Следовательно, для идеально чистых металлических поверхностей (оптически прозрачная оксидная пленка) характер обработки этой поверх­ности сказывается на скорости тепловыделения более заметно, чем изменение действующего начального давления.

Рассмотрим теперь общую тепловую картину не только в зоне свариваемого контакта, но и целиком в свариваемых деталях. Согласно обозначениям на рис. 2.26, можно составить баланс энергии в таком виде.

К концу процесса, когда расплавлено цилиндрическое ядро диаметром dT и высотой А, на эту операцию затрачена энергия

QK = 4P()Tht/(nc%). (2.80)

Эта энергия расходуется на плавление металла ядра и тепловые потери. Их можно определить: энтальпия

тепловые потери в массу свариваемых деталей 9м = 4тГпя уїф S УТ.

Полагая S — 3x^28, перепишем

ди = 8тпТап У Кус dT8 У і. (2.82)

Рассмотрим отношение энергий (2.80) к (2.82)

QK ___ _________ 4P(>Tht_____ _ /2рт/г % УТ

9м mdr$nmTnn VWcd^b J/T 8mn2dftTim ’

Из этого отношения можно получить критерий технологиче­ского подобия, если учесть несомненную пропорциональность Р = aTd|, в которой Р — сила сжатия электродов. Тогда:

— Ki УТо = К;

УМ

/*"( '..Я j/” / Oiji

йтТ’пл 6Р

Из рис. 2.26 видно, что при точечной сварке имеются еще два очага тепловыделения, это контакты электродов с деталями QgM. Очаги эти весьма своеобразны. Прежде всего энергия Q3M регу­лируема. Интенсивность тепловыделения в этих несваривающихся контактах зависит от формы и размера электродов, металла элек­тродов, состояния поверхности. Эти же факторы определяют и отвод теплоты в массу охлаждаемого электрода q3.

Температура поверхности металла под электродом Т'пм всегда больше температуры поверхности электрода Тэ. Разность Тпм — —Тэ может доходить до 200—300°, если наконечники электрода недостаточно часто подвергают зачистке или же поверхность свариваемого металла покрыта заметным слоем оксидов.

Если записать в общем виде тепловой баланс точечной сварки, то можно ограничиться таким равенством:

Qv 2Qsm = 9то 4~ Ям 4~ 2<7э" (2.85)

Здесь, как уже неоднократно отмечалось, только слагаемое QK представляет собой, с точки зрения расчета, наиболее стабиль­ную величину. Все остальные вносят, каждое по-своему, в тепло­вой баланс иногда значительную неопределенность. Борьба G этими неопределенностями и с нестабильностью всех переменных и является целью при разработке технологии контактной точеч­ной сварки.

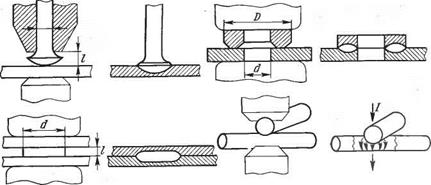
На рис. 2.26 изображена классическая схема точечной сварки. Однако в реальной действительности создаются такие конструк­тивные сочетания, как, например, показанные на рис. 2.27, для которых форма расплавленного ядра — совсем не цилиндр. Ра-

Рис. 2.27. Некоторое типы рельефно-сварных соединений

зумеетея, в случаях такого рода тепловой баланс (2.85) может быть весьма своеобразным и формулы тепловыделения, если только такие формулы нужны, будут отличаться от (2.80). Кон­структивные сочетания типов, приведенных на рис. 2.27, принято относить к разряду рельефной сварки, поскольку в каждом ва­рианте свариваемый контакт отличается рельефным выступом той или иной формы. Выступы такого рода играют заметную роль концентраторов энерговыделения, за счет чего и удается осуществ­лять расплавление ядра разной формы. Это обусловливается не только конструкцией свариваемых деталей. Более существен­ное значение имеет распределение сварочного тока в процессе нагрева свариваемого (да и не только свариваемого) контакта.

Форма свариваемых деталей, магнитность или немагнитность металла, резкие изменения токопроводящих сечений проводника — все эти вещи, вместе взятые, создают иногда весьма сложную картину распределения тока в свариваемых деталях. Во многих случаях оно оказывается подобным тому, которое характерно для распределения механических напряжений по растягиваемым или сжимаемым деталям разной формы, с разными концентраторами напряжений.

Этот факт в некоторой мере поясняют модели, приведенные на рис. 2.28. На первой из них (рис. 2.28, а) показаны эпюры рас­пределения сварочного тока по плоскостям 2—2 свариваемого и 1—1 несвариваемого контактов. При сильном эффекте шунтиро­вания тока в соседнее ядро (рис. 2.28, б) эпюры токов резко ме­няют свою форму. На рис. 2.28, г показана разная степень кон­центрации тока относительно разной формы надрезов и изгибов проводящей шины. При окончательном формировании контакта (рис. 2.28, д) характерно уменьшение концентрационных пиков тока в тех плоскостях 2—3, где плотности тока вообще весьма ве­лики по сравнению є плоскостями 1—1.

Рис. 2.28. Схемы возможных концентраций сварочного тока при одноточечном (а) и многоточечном (б) сварном соединении; при надрезах различной формы (в); при искривленных проводниках (г) и в плоскости контакта в момент включения тока (б)

2.5. 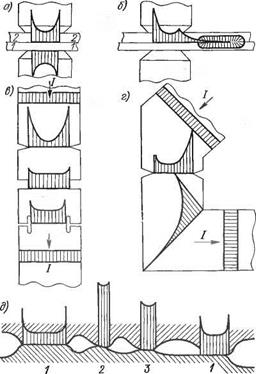Особенности нагрева металла при шовной сварке

Шовно-сварные соединения представляют практический ин­терес, если необходима не только определенная прочность, но и достаточная плотность или даже полная герметичность. Такого рода соединения могут быть получены заменой электродов точеч­ных машин вращающимися роликами (рис. 2.29, здесь диаметр ролика показан значительно преуменьшенным по сравнению с тол­щиной свариваемых листов, кроме того, изображен только один верхний ролик). Рис. 2.29 иллюстрирует процесс сварки так назы­ваемым шаговым швом, когда при неподвижном ролике включается импульс сварочного тока, за счет которого происходит формиро­вание единичной сварной точки. Сваривающий ролик поворачи­вается на некоторый угол (от штрихового изображения) и оста­навливается для постановки следующей точки. Линейное переме­щение ролика осуществляется на такой шаг, чтобы получалось перекрытие предыдущей точки каждой последующей на размер k. Минимальный размер перекрытия к, согласно ГОСТ 15878—79, должен быть не менее V4 от длины литого ядра, если толщина по

листов более 0,6 мм. Для меньших толщин допускают­ся меньшие перекрытия. Соб­ственно сваривающий ток /св (рис. 2.29) частично шунти­руется в предыдущую точку.

В современной производ­ственной практике наиболь­шее распространение полу­чил цикл шовной сварки так называемым прерывистым процессом, когда ролики вра­щаются безостановочно, а сварочный ток включается на время /ш после некоторой паузы tn. Каждая единичная точка в таком цикле полу­чается удлиненной. На рас­смотрении этого процесса следует остановиться, по­скольку далеко не все пони­мают электротепловую кар­тину прерывистого способа шовной сварки. Здесь осо­бенно характерно проявляют­ся два особых электрических эффекта, рассмотренные выше для то­чечной сварки: явление шунтирования сварочного тока и сжатие линий тока его собственным магнитным полем. Для анализа всей этой картины воспользуемся рис 2.30. На рис. 2 30, а показана

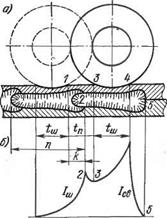
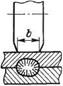
Рис. 2.30. Сварной шов при прерывистом включении сва­рочного тока и непрерывном вращении роликов (й), рас­пределение тока в металле (б) и схема действия продоль­ного (РЬ) и поперечного (рп) давления магнитного поля Н на протекающий по металлу ток (в)

схема перемещения роликов (опять без соблюдения масштаба диа­метра ролика и толщины свариваемых деталей). Непропорцио­нально глубоко вдавлены ролики в свариваемые детали. Рассмо­трим момент, когда ролики после сварки точки длиной п передви­нулись из положения ролика, изображенного штриховой линией, в позицию, показанную сплошной линией. Он достаточно плотно контактирует с металлом по длине от линии 3 до линии 4. В этот момент и включается импульс тока длительностью tm - Как видно из рисунка, за время tn (время вращения ролика без тока от ли­нии 1 до линии 2) успел образоваться непроверенный участок, от линии 2 до линии 3. Вот этот участок и сваривается, но только за счет тока шунтирования /ш, который по своей плотности рас­пределяется в момент включения сваривающего тока по эпюре, показанной на рис. 2.30, б.

Как видно, ток шунтирования бесполезный и даже вредный при точечной сварке, для шовной сварки превращается в свою противоположность и оказывается решающим в деле создания плотного шва посредством перекрытия каждой последующей точкой точки предыдущей.

Не последнюю роль в деле шунтирования играет и эффект магнитного давления. Ролик — это не электрод точечной машины. Его контактирование с металлом происходит по удлиненной пло­щади, когда размер п больше ширины ролика Ь (иногда значи­тельно). Это и является причиной неравномерности давления, оказываемого на линии тока собственным магнитным полем этого тока. А это приводит к вытягиванию тока и в сторону шун­тирования его в предшествующую точку, и в сторону движения ролика в еще несваренный участок.

Вот по этим двум причинам (шунтированию и магнитному сжатию тока) и удается время паузы tn (движения ролика без тока) устанавливать не только равным времени включения tm, но иногда даже делать ta > /ш, и, несмотря на это, получать плот­ный шов с достаточным перекрытием k.

Рассмотрим количественную сторону процесса сварки швом посредством прерывистого включения тока. Согласно ранее ис­следованным соотношениям, был определен физический смысл критерия К- Так, согласно (1.47) и (2.83) числитель этого крите­рия — это та энергия, которую мы вводим в зону свариваемого контакта, а знаменатель — энергия, теряемая за счет теплопро­водности в окружающую массу металла. Для шовной сварки можно считать

<Э« = /2Рт^ш/^ТШ»

где I — ток вторичного контура, т. е. сваривающий и шунтирую­щий; рт — удельное сопротивление металла в момент его плавле­ния; к — высота расплавленного ядра; йтт — диаметр такой еди­ничной точки, которая по площади эквивалентна тоже единич­ной, но некруглой точке, какую ставит неподвижный ролик.

Потери энергии в металл, которые происходят уже не только за время сварки tm, но и за время паузы tn,

Яы — Тая ~/кус S /ш -|- /п.

В этом равенстве площадь S, через которую теплота отводится теплопроводностью,

S = пб,

где б — толщина свариваемого металла, а длину точки п, как видно, приближенно можно выразить через линейную скорость движения роликов v и время включения тока tm, т. е. п = vtm. Тогда S = vtm6.

Если так же, как и при точечной сварке, написать

^тш = Р/От,

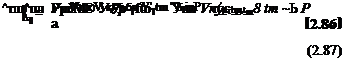где Р — сила сжатия роликов, а ат — предел текучести холодного металла, то получим

По аналогии с точечной сваркой справедливо, по-видимому, силу тока 1 назначать по формуле типа (см. гл. 4)

I = AdTm/-/~pT, (2.88)

что будет проверено на расчетных примерах.