Межзонные электронные переходы
 2 марта, 2014
2 марта, 2014  admin
admin Для вычисления формы спектров излучательной рекомбинации и скоростей рекомбинации полезно рассмотреть поглощение вблизи края основной полосы и воспользоваться принципом «детального равновесия». Форму края поглощения можно рассчитать для случая как прямых, так и непрямых переходов в отсутствие примесных уровней. Этот вопрос освещен в целом ряде работ [12—16], поэтому здесь приводятся только конечные результаты. Для разрешенных (по соображениям четности) прямых переходов в полупроводнике со сферическими изоэнергеги - ческими поверхностями коэффициент поглощения а равен
|
(3.1) |
|
где |
|
(3.2) |
|
а = лА Аел& (Av — Eg)‘/!/sih An, A = [Ex/(hv-Eg)} |
а Ех — энергия связи свободного экситона.
Для случая Av— Eg^n2Ex выражение (3.1) упрощается:
|
(3.3) |
|
где |
|
(3.4) |
|
a = A (Av — Eg)'1', A. е2(2ц),/! f ncmh2 " |
Здесь f — сила осциллятора для данного перехода, ц = “ "t - m*h) — приведенная эффективная масса плотно-
ТЕОРИЯ ИЗЛУЧАТЕЛЬНОЙ РЕКОМБИНАЦИИ
|
99 |
сти состояний, п — показатель преломления, с — скорость света.. Для прямых переходов / имеет величину порядка Iі). Следует отметить, что, поскольку а~ (АЕ)'/2 [выражение (3.3)], эта величина пропорциональна плотности состояний,. вычисленной без учета взаимодействия между носителями [выражение (2.1)]. Кулоновское взаимодействие носителей деформирует волновые функции электронов и дырок так, что а становится большим и почти не зависит от hv при hv ~ Еч, вместо предсказываемого выражением (3.3) уменьшения по степенному закону до нуля. Кроме того, электронно-дырочное взаимодействие приводит к появлению дискретных состояний свободного экситона с энергией, несколько меньшей Eg (рис. 3.3).
Экситонные эффекты также играют большую роль в непрямозонных полупроводниках в области вблизи края собственного поглощения. В этом случае закон сохранения квазиимпульса выполняется благодаря поглощению или испусканию фонона с энергией hoi и соответствующим волновым вектором кр, так что
к, = кс-к,. (3.5)
При низких температурах происходит только испускание фононов. Для разрешенных (по соображениям четности) непрямых переходов с образованием свободного экситона
а —В (hv — Eg + Ех — /ko)v (3.6)
а для переходов электронов в зону проводимости в состояния намного выше дна зоны
а = С (hv — Eg — Лео)2. (3.7)
Постоянные В и С содержат энергетические знаменатели вида [(£с)г, — (^с)х, Т> Где Ес — энергии зоны проводимости, определенные в соответствующих точках приведенной ■ зоны
|
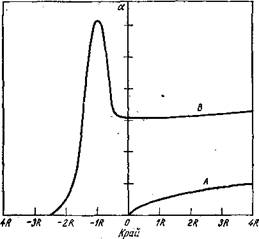
Рис. 3.3. Форма края основной полосы поглощения без учета (А) и с-учетом (В) экситонных взаимодействий. Энергия по оси абсцисс выражена в постоянных Рндберга для экситона R=(ie4/2ft! eJ, где )*—приведенная масса электронно дырочной пары [выражение (2.4), в котором т* заменено, на ц]. |
Бриллюэна для обратной решетки (рис. 3.2). Появление этого члі на объясняется тем, что коэффициент поглощения для непрямых переходов вычисляется с помощью теории возмущений второго порядка в предположении, что рассеяние электрона (или дырки) происходит через соответствующее промежуточное состояние в разрешенной зоне. Этот множитель и правила отбора для взаимодействия с фононами различных типов симметрии определяют, какой из возможных вариантов непрямого перехода преобладает. Например, в GaP наиболее вероятен переход через промежуточное состояние, связанное с наинизшим Гі-миниму - мом зоны проводимости, однако этот переход возможен только при рассеянии на продольных акустических фононах [17, 18]. Такую зависимость вероятности рекомбинации в непрямозонных полупроводниках от точной формы зоны проводимости и валентной зоны вдоль соответствующих направлений в /г-пространстве (т. е. направлений, на которых находятся абсолютные минимумы), мы будем называть эффектом зонной структуры.
Закон сохранения квазиимпульса может выполняться также благодаря рассеянию носителей на примеси. В выражение для а и в этом случае входит тот же энергетический знаменатель. Из-за малой величины энергетического зазора (Гі)с—*,№)с в GaP рассеяние электрона через промежуточное состояние, связанное с (Гі)с, представляет по-прежнему наиболее вероятный переход, поскольку в выражение для вероятности перехода входит указанная разность энергий в знаменателе. Морган [18] показал, что симметрия J-минимума зоны проводимости в GaP зависит от того, в каком узле (Ga или Р) находится притягивающая электрон примесь (донорная или изоэлектронная примесь замещения, которая образует или почти образует связанное состояние для электрона). В работе сделан вывод о том, что существенно увеличить вероятность межзонных переходов в GaP могут только притягивающие электрон примеси, которые занимают узлы Р. Известно много экспериментальных данных, подтверждающих этот вывод (разд. 3.2.2, 3.2.6 и 3.2.7).
Энергия ионизации доноров, связанных с непрямыми Х-мини - мумами, как это имеет место в GaP, составляет величину порядка 100 мэВ. Ниже будет видно, что эта величина намного больше энергии ионизации уровней, связанных с Г-минимумом в типичных прямозонных полупроводниках, например в GaAs (разд. 3.3) Ed « 6 мэВ. Это различие обусловлено двумя взаимосвязанными причинами. Во-первых, в Г-минішуме эффективная масса электрона намного меньше; в GaAs она составляет ~0,066/по, а в GaP равна ~ 7зяіо (масса проводимости). Согласно k • р-теории [18а], эффективная масса в Г-минимуме быстро растет с увеличением ширины запрещенной зоны, так что Ео ~ 40 мэВ в GaN, где Eg & 3,4 эВ (разд. 3.5.2), что согласуется с результатами, следующими из уравнения (2.4). Во-вторых, поскольку плотность волновой функции электрона в центральной ячейке примесного иона уже намного больше, когда масса т* велика, что наблюдается в Х-минимуме, энергия ионизации донора дополнительно возрастает из-за так называемого взаимодействия центральной ячейки или химического сдвига [53]. Это увеличение энергии ионизации сказывается больше всего на основном состоянии донора из-за сильного влияния, оказываемого на плотность электронов в центральной ячейке формой огибающей волновой функции донора. Непосредственное влияние оказывает и только что рассмотренный эффект зонной структуры, который важен только для уровней, связанных с боковыми минимумами, где фазовая волновая функция электрона отлична от нуля [18]. Для типичных значений энергии ионизации донора в GaP (100 мэВ) химический сдвиг увеличивает энергию ионизации более чем вдвое по сравнению с энергией, определяемой эффективной массой (~45 мэВ, табл. 3.1). Возможны и еще большие отклонения от энергии ионизации, определяемой эффективной массой; примером может служить донор - ный центр О в GaP, для которого Ев примерно в 18 раз больше рассчитанной по эффективной массе [36]. В разд. 3.2.8 показано, что люминесцентные свойства GaP в красных светодиодах тесно связаны с существованием этого аномально глубокого донора.
|
Таблица 3.1 Энергии ионизации доноров и акцепторов в GaP *
') Энергии нонизацнн мелких доноров и акцепторов получены в приближении эффективной массы, согласно расчету Фолкнера [35]. Значение энергии ионизации донора требует уточнения в связи с результатами проведенных экспериментов по определению эффективной массы электронов методом циклотронного резонанса [35а]. Вычисление энергии возбужденных состояний с помощью простого набора параметров (что легко реализуется в Si и Ge) в GaP затруднено [34,35]. Это, возможно, связано с сильной непараболич - ностью, возникающей из-за того, что вблизи точки X нижний минимум зоны проводимости имеет не простую форму, показанную на рис. 3.2, а «двугорбую структуру» [35а, 356]. Такая сложная форма минимума может объяснить появление дополнительной структуры в спектрах люминесценции экситонов, связанных на акцепторах [56]. '2) Значения определены по данным для S и Те с учетом разности в энергиях связи доноров IV группы, рассчитанной по «двухэлектроиным» спектрам [37]. 3) Акцепторный уровень неизвестного происхождения. — Прим. перев. |
Приемлемые теоретические обоснования энергий связи столь глубоких состояний приведены в работе [36а].

 Опубликовано в
Опубликовано в