Стационарные методы

Благодаря своей простоте стационарные методы все еще имеют значительное распространение, несмотря на целый ряд свойственных им недостатков.

Для определения коэффициента теплопроводности в ста­ционарных условиях необходимо точно определить величину теплового потока через образец и разность температур на гра - 66

Ницах или в других точках образца. Коэффициент теплопровод­ности рассчитывается по следующим формулам: для плоского образца

/.= (IV.7)

Г Л/х * ' '

Для цилиндрического образца (тепловой поток распростра­няется по радиусу цилиндра)

Х (?1п(г2/л)_. му 8)

Для сферического образца •

» ^9)

Где б — толщина образца (поперечный размер); Р — площадь его сечения, перпендикулярного к направлению теплового по­тока; С} — количество тепла, прошедшего от поверхности с температурой Т1 к поверхности с температурой Т2(Т—Г2 = ЛГ); I — длина цилиндрического образца; г2 и Г— наружный и внутренний радиусы цилиндрического и сферического образцов; т — продолжительность опыта (в тех случаях, если измеряется мощность теплового потока, время в расчетных формулах не фигурирует).

Формулы (1У.7) — (1У.9) выведены для одномерного теп­лового потока. Поэтому достоверность результатов зависит от того, в какой степени это допущение справедливо в каждом конкретном случае. Для приближения к одномерному тепло­вому потоку поперечные размеры образца стремятся выбирать значительно меньшими, чем продольные (отношение не менее 1 : 10). Часто для предотвращения утечек тепла, искажающих температурное поле, а также для того, чтобы иметь возмож­ность определять мощность теплового потока по электрической мощности нагревателя, образцы и нагреватели окружают так называемыми охранными приспособлениями с отдельными нагревателями. Их температура поддерживается равной тем­пературе основного нагревателя.

На рис. 14 изображена схема установки, примененной М. Вике « В. Петерсом [29], для определения теплопроводно­сти монолитных образцов углей и коксов в интервале темпера­тур 50—200° С.

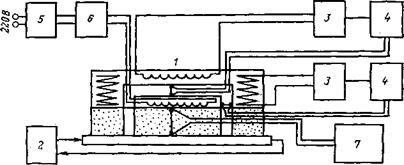
Образец в виде цилиндра диаметром 18 мм зажимается между двумя параллельными серебряными пластинами. Ниж­няя пластина, охлаждаемая циркулирующей жидкостью, име­ет постоянную температуру, которая задается при помощи тер­мостата. Температура верхней пластины изменяется путем ре­гулирования тока, поступающего в нагреватель от выпрямите­ля. Прибор снабжен охранными приспособлениями кольцевого

Рис. 14. Схема прибора для определения теплопроводности углей и коксов В интервале 50—200° С: ) — прибор; 2 — циркуляционный термостат; 3 — трансформатор пнтания охранных при­способлений; 4—усилитель постоянного тока; 5 — разделительный трансформатор; & — источник постоянного тока; 7 — милливольтметр

Типа с нагревателями, питаемыми переменным током от вариа - торов. Вариаторы управляются усилителем постоянного тока, сигнал на который поступает от дифференциальных термопар, смонтированных на основном нагревателе и нагревателях ох­ранных приспособлений. Благодаря этому температуры нагре­вателей поддерживаются одинаковыми, что обеспечивает од­номерность температурного поля в образце и определение теп­лового потока с требуемой точностью.

Отличительной особенностью рассматриваемого метода яв­ляется применение масляной смазки для улучшения теплового контакта между пластинами и поверхностью образца. Так как, проникая на некоторую глубину в испытуемый материал, масло изменяет теплопроводность его. на этом участке, такой прием требует специальных опытов по определению оптимальной толщины образца, при которой этот эффект практически не­ощутим.

Описанный метод является абсолютным, так как не требует применения какого-либо эталона. На практике часто применя­ются также сравнительные стационарные методы, позво­ляющие исключить определение теплового потока.

Пусть, например, пластина из испытуемого материала с теп­лопроводностью А* помещена между двумя пластинами тех же размеров из материала с известной теплопроводностью Яэ - Оче­видно, что тепловой поток через вое пластины одинаков. Вы­разив его через температурный перепад на одной из эталонных пластин АГэ и подставив в формулу (1У.7), получим

<1УЛ0>

Где АТх — перепад температуры на образце.

Аппаратурное оформление сравнительных стационарных ме­тодов, как правило, проще. Недостатком их является необходи­мость обеспечения надежного теплового контакта по большему числу поверхностей.

Методы регулярного теплового режима

Известно, что тело, имевшее до начала опыта произвольное распределение температуры, будучи погруженным в среду с постоянной температурой, через некоторое время начнет нагре­ваться или охлаждаться таким образом, что относительное из­менение температуры в любой его точке не будет зависеть от времени и координат, а будет определяться только коэффици­ентом температуропроводности и условиями теплообмена со средой. Такой режим называется регулярным и во времени яв­ляется переходным между предшествующим чисто нестацио­нарным и последующим стационарным режимами.

Температурное поле внутри образца на стадии регулярного режима можно найти, решая уравнение теплопроводности (IV.!) при начальном условии

Т (-_0) =/(х, У, 2)

И граничных условиях

Тс = const,

Где т — время; п — нормаль к поверхности тела; R — определяю­щий размер образца (радиус шара, цилиндра или полутолщина пластины); а — коэффициент теплоотдачи, характеризующий теплообмен между поверхностью тела и окружающей средой; Тс — температура среды; Гп — температура поверхности об­разца.

Приближенное решение имеет вид [47]

- ЛФ (Р, 4-) ехр (IV. U)

Где Г0 — начальная температура в некоторой точке тела; А — постоянная; Ц1 — первый корень характеристического уравне­ния; а — коэффициент температуропроводности; х — коорди­ната.

Логарифмируя и дифференцируя уравнение (IV.11) по вре­мени, получаем

Д[1п(Гс— Г)] а

Дт — ’

Отсюда, обозначив с([1п(Тс—Т)]/йт = —т (темп нагрева или охлаждения), найдем основную расчетную формулу метода

(IV. 12)

Поскольку при регулярном режиме /л = const и в логарифми­ческих координатах изменение во времени избыточной темпе­ратуры выражается прямой линией, постольку темп нагрева можно найти либо графически как тангенс угла наклона меж­ду осью абсцисс и указанной прямой, либо расчетом по фор­муле

(IV.13)

N In (Гс - Г,) - In ( Гс - Т2)

Где ТI и Гг — температура в некоторой точке образца, измерен­ная в моменты времени п и тг от начала регулярного режима.

В общем случае величина ць входящая в расчетную фор­мулу (IV. 12), зависит от формы тела и критерия Био (Ш = = ак/Х). Чтобы обойти связанные с этим затруднения, образ­цам придают простые геометрические формы и принимают меры для возможного увеличения коэффициента теплоотдачи так, чтобы В1->-оо. Практически это достигается, например, погружением образца в циркулирующую жидкость.

При выполнении условия В1-»-оо расчетные формулы для образцов различной формы записываются следующим образом для шара радиусом к

(IV.14)

Для бесконечного цилиндра радиусом R

(2,41/У?)2 + (*/Л)2 •

(IV. 15)

Для цилиндра конечных размеров радиусом R и высотой h

M

(IV.16)

В настоящее время известно несколько вариантов метода, позволяющих определить коэффициенты температуро - и тепло­проводности, а также оба эти коэффициента одновременно.

В приборах, предназначенных для измерения коэффициента температуропроводности и называемых а-калориметрами, ре­гулярный режим реализуется при условии В1-»-оо. Образец помещается в тонкостенный сосуд соответствующей формы, из­готовленный из хорошо проводящего материала. Внутри об­разца располагается один из спаев дифференциальной термо­пары. Другой спай помещается в окружающую образец среду. Собранный таким образом калориметр погружается в термо - 70

Стат, заполненный тающим льдом, маслом или другой жидкостью, температура кото­рой тем или иным способом поддерживает­ся постоянной во времени и по объему тер­мостата.

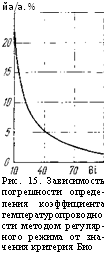
Йа/а. % Рис. 15. Зависимость погрешности опреде­ления коэффициента температуропроводно­сти методом регуляр­ного режима от зна­чения критерия Био

Опыт состоит в снятии кривой охлажде­ния (нагревания) образца 7’=/(т), последу­ющем вычерчивании графика 1п7’=/(т) и вычислении для прямолинейного участка, отвечающего регулярному режиму, темпа охлаждения (нагревания) и коэффици­ента температуропроводности [формулы (IV.14) — (1У.16].

Из сказанного выше ясно, что методиче­ская ошибка определения температуропро­водности в а-калориметре зависит главным образом от того, как выполняется условие В!—>"Оо (рис. 15). Немалое влияние на ре­зультаты определений оказывают также термические сопротивления между оболоч­кой и образцом [47].

Определение коэффициента теплопроводности по методу ре­гулярного режима более громоздко, так как оно проводится в условиях конечного и небольшого значения критерия Био, по­этому необходимо определение коэффициента теплоотдачи. Тео­рия и методика таких измерений подробно изложены в лите­ратуре [39, 47] и здесь не рассмотрены, так как из-за сложно­сти метод имеет ограниченное распространение.

Методы квазистационарного теплового режима

Главным достоинством рассматриваемых методов является возможность определения температурной зависимости коэффи­циента температуропроводности в широком температурном ин­тервале.

Если тело, имеющее произвольное начальное распределение температуры, поместить в среду, температура которой линейно возрастает во времени, то через некоторое время после начала опыта температура тела во всех его точках (сначала на пери­ферии, а затем и в центре) станет изменяться по тому же за­кону. При этом в теле формируется стационарное или близкое к таковому поле градиента температуры, зависящее от формы тела, скорости нагрева и теплофизических свойств материала. Квазистационарный режим может быть создан как при линей­ном изменении температуры среды или поверхности тела (по­следнее предпочтительнее), так и при постоянном тепловом по­токе через поверхность.

Опыт по определению коэффициента температуропроводно­сти методом квазистационарного теплового режима сводится к измерению фактической скорости нагрева Ь и градиента тем­пературы. Последний вследствие предполагаемого его постоян­ства заменяется обычно конечной разностью температур АТ между двумя точками, удаленными на разное расстояние от оси симметрии тела. Так, для бесконечного цилиндра радиусом

А = Ь-Г±т-} , (IV.17)

Где г 1 и г2 — расстояния от оси цилиндра до точек, в которых измеряется температура (Г1 <г2). В частности, если Г] = 0, г2 = Я, то расчетная формула для коэффициента температуропровод­ности упрощается:

Ш2 (IV. 18)

А

Аналогично для пластины (диска) бесконечной протяжен­ности толщиной 2 к при измерении температурного перепада между одной из ограничивающих плоскостей и осевой плос­костью

Ь№ , т, г 1Г1.

А==! 2дг ' (IV.19)

Температурное поле в образцах конечных размеров тем сильнее отличается от одномерного температурного поля, чем

Меньше отношение й = й/Я для цилиндра и чем оно выше для

Пластины. В связи с этим возникает вопрос об оптимальном соотношении геометрических размеров образца, позволяющем с достаточной точностью оперировать одномерными зависимостя­ми, из которых получены расчетные формулы (ГУ.17) — (1У.19).

Если скорость нагрева образца конечных размеров на всех поверхностях одинакова, неодномерность температурного поля в нем может быть учтена введением в расчетные формулы ко­эффициента Е, являющегося функцией к. Тогда для ограниченного цилиндра

ЬЮ (1^20)

А = Е

Д т

И для диска конечных размеров

(ІУ.21)

Ьк2

А = Е-

Дг

Зависимость коэффициента Е от параметра й приведена в табл. 1У.2.

При й = 3 для цилиндра и к = 1/^ для диска погрешность, выз­ванная неодномерностью температурного поля, становится пре­небрежимо малой (см. табл. 1У.2).

Таблица ІУ.2

Значения коэффициента Е, учитывающего неодномерность температурного поля в образцах конечных размеров [47]

Цилиндр |- Диск * = ВД 1 2 3 * 1/2 1/3 1,4 0 0.2006 0,2454 0,2496 0,25 0,4056 0,4752 0,4928 0,5

На практике иногда вместо температурного перепада АТ определяют время запаздывания Ат температуры в центре об­разца по сравнению с температурой на периферии. Поскольку Т :ЬХ,

Я = £-гг. (™.22)

Известно, что теплофизические свойства всех твердых тел изменяются с ростом температуры. Поэтому даже при безуко­ризненном соблюдении линейного закона разогрева на поверх­ности образца скорость подъема температуры в его централь­ной области непрерывно изменяется. Это особенно заметно при широкотемпературных измерениях. Строго говоря, квазиста - ционарный режим при этом нарушается, так как градиент тем­пературы изменяется во времени и по объему образца. Тем не менее, формулы (IV.20) и (1У.21) можно применить без сущест­венной погрешности, если рабочую диаграмму опыта разделить на отдельные участки, в пределах которых коэффициент темпе­ратуропроводности остается практически постоянным.

По этой же причине скорость нагрева должна выбираться такой, чтобы при фиксированных координатах Г и г% темпера­турный перепад АТ не превышал некоторой предельной наперед заданной величины. Так, например, для углей и других твердых горючих ископаемых предельным можно считать пере­пад, равный 8—10° С. Общее правило состоит в том, что пере­пад АТ следует поддерживать настолько малым, насколько это позволяет регистрирующая аппаратура.

Аналогичным образом, т. е. разбивая рабочий интервал из­мерений на небольшие участки, можно поступать при неболь­ших отклонениях скорости нагрева поверхности образца от требуемого постоянства,