Рассеяние размеров деталей, обрабо­танных на налаженном станке, и законо­мерность этого рассеяния могут быть наглядно установлены при помощи кри­вых распределения на основе закона больших чисел.

Совокупность значений действитель­ных размеров заготовок, обработанных при неизменных условиях и расположен­ных в возрастающем порядке с указанием частоты повторения этих размеров и частостей, называется распределением размеров заготовок.

Под частостью понимают отношение числа заготовок одного размера к общему числу заготовок партии.

Кривые распределения строят так. Измерив все обработанные заготовки в партии, разбивают их на группы с одина­ковыми размерами или отклонениями (в пределах определенного интервала). Час­тость в этом случае представляет собой отношение числа заготовок, действитель­ные размеры которых попали в данный интервал, к общему количеству п изме­ренных заготовок в партии. Например, после измерения 350 заготовок с действи-

" 1 2 J 4 5 6 7 8 9 10 Номер группы (диаметры)

Рис. 12.9. Распределение размеров обработан­ных заготовок в партии: 1 — действительное распределение; 2 — кривая нормального распределения

Тельными размерами в пределах 49,940— 50,000 мм распределение их размеров может иметь вид, приведенный в табл. 12.3. Эти результаты можно пред­ставить графически: по оси абсцисс откладывают интервалы размеров (или номера групп) в соответствии с табл. 12.3, а по оси ординат — соответствующие им частоты т или частости т/п. В резуль­тате построения получается ломаная линия (рис. 12.9). При большом числе изменений эта ломаная линия прибли­жается к плавной кривой, которая назы­вается кривой распределения.

При разных условиях обработки заготовок рассеяние их размеров подчи­няется различным математическим за­конам. В технологии машиностроения

Таблица 12.3. Распределение размеров обработанных заготовок в партии (я = 350 шт.) Номер груп­пы Интервал размеров, мм Час­тота повто­рения Т Частость Т/п. 1 49,940—49,946 8 0,023 2 49,946—49,952 16 0,046 3 49,952—49,958 25 0,071 4 49,958—49,964 65 0,186 5 49,964—49,970 85 0,242 6 49,970—49,976 73 0,208 7 49,976—49,982 48 0,137 8 49,982—49,988 24 0,069 9 49,988—49,994 6 0,017 10 49,994—50,000 0 0,000

Практическое значение имеют следующие законы распределения (рис. 12.10).

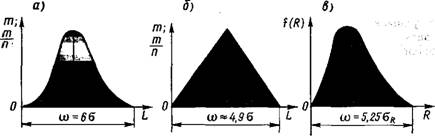
1. Нормальный закон (закон Гаусса). Центры рассеяния размеров во вре­мени не смещаются. Этому закону (рис. 12.10, а), подчиняется распределе­ние линейных размеров (диаметров D, длин L) и угловых размеров обрабаты­ваемых заготовок.

2. Закон равнобедренного треуголь­ника (закон Симпсона). Он (рис. 12.10,6) описывает рассеяние случайной вели­чины, если на нее действуют два доми­нирующих фактора, каждый из которых равномерно распределен.

Рис. 12.10. Законы распреде­ления размеров обработанных заготовок: а — нормальный (закон Гаусса); б — Симпсо­на; в — Рэлея; г — равной ве­роятности; д — композиция нормального закона и закона равной вероятности (х, — Случайная величина)

3. Закон эксцентриситета (закон Рэ- лея). Распределение таких существен­но положительных величин, как эксцент­
риситет, биение, разностенность, откло­нения от параллельности, отклонения от перпендикулярности, овальность, конусо - образность, отклонение от соосности, торцовое и радиальное биения и др., подчиняется закону эксцентриситета. Из рис. 12.10, в видно, что для теоретической кривой распределения по закону Рэлея характерны крутой подъем восходящей ветви и более пологий спуск нисходящей ветви. Фактическое поле рассеяния со значений переменной случайной вели­чины радиуса-вектора R (эксцентриси­тета, разностенности и т. п.) находят по формулам:

Ш = 5,25(Тй; со = 3,44<то,

Где aR — среднеквадратическое отклоне­ние переменной случайной величины R-, оо — среднеквадратическое отклонение значений координат х и у конца радиуса - вектора R.

4. Закон равной вероятности (рис. 12.10, г) наблюдается, когда на случайную величину действует домини­рующий фактор, равномерно возрастаю­щий по времени, например переменная систематическая погрешность, связанная с изнашиванием режущего инструмента. Закон равной вероятности распростра­няется на распределение размеров заго­товок повышенной точности (5-6-й ква - литеты).

5. Композиции законов распределе­ния. Если при обработке заготовок одновременно воздействуют разные фак­торы, то возникают как случайные погрешности, подчиняющиеся разным законам, так и систематические. На рис. 12.10, с) приведена композиция нормального закона и закона равной вероятности. Композиции находят мето­дами математической статистики.

Многочисленные исследования пока­зывают, что если работа протекает в нормальных условиях на налаженных станках, то распределение действитель­ных размеров деталей в партии подчи­няется, как правило, закону нормального распределения (закону Гаусса). Рас­смотрим его подробнее.

Уравнение кривой нормального рас­пределения имеет вид

16 Зак. 338

У = <р(х) = о~1 (2л) ~ |/2ехр [—х1/ (2а2) ],

' (12.1)

Где у — частота появления погрешности; а — среднеквадратическое отклонение аргумента, равное квадратному корню из средней арифметической квадратов всех отклонений; х — отклонение дейст­вительных размеров от средних, x = L,— — Lcp (Li — действительные размеры; LcР — среднее арифметическое значение действительных размеров заготовок дан­ной партии).

Средний размер детали в партии Lcp (мм) равен среднему арифметическому из размеров всех деталей всех групп:

Z. Cp= (m, Li + M2L2-f ... + NikLk) /П =

K

= ( I Liin^/N, (12.2)

Где гп, m2, ..., т. к — частота (количество деталей в каждой группе); L, L2, ..., Lt — размеры отдельных групп деталей, соответствующие числу интервалов; п = = т. 4- Ш2--... 4- Шк — общее количество измеренных деталей в партии; K — число групп, соответствующее числу интер­валов.

Среднеквадратическое отклонение оп­ределяют по формуле

А= [(mix?4-(712*24-...4-ТкХк)/п] 1/2 =

= {[m,(Li — Lcp)2 + m2(L2— Z. cp)24- ••• +

4-M*(Z.*-Z. cp)2]/«}'/2={[ J (L,-

;=t

К

— Lcp) 2т,1//г|'/2 = |Y £ *,W)/n"K

J ' LV ;=i ' J (12.3)

Где Xi = Li—Lcp; x2 = L2 —Lcp; ...; Xk = = Lk — Lcp — отклонения действительных размеров от среднего арифметического в каждой группе деталей.

Параметр Lcp (математическое ожи­дание) определяет центр группирования размеров, параметр о — рассеяние их относительно центра. Поясним сказан­ное графически.

Горизонтальная ось на рис. 12.11, а — ось L. Будем последовательно отклады­вать на ней размеры L, от начала коорди­
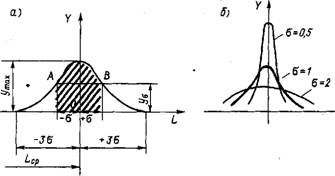
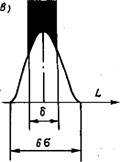
нат. Поскольку размеры не равны между собой, их правые концы не совпадают, а рассеиваются на некотором участке оси L. Величина Lop определяет центр рассеяния размеров. Размеры рассеи­ваются симметрично относительно цент­ра, и большинство из них укладывается в область ±3сг. За пределы поля рассея­ния 60 выходит лишь 0,27 % всех разме­ров, что практически вполне допустимо. Кривая на графике называется кривой нормального распределения, она иллюст­рирует закон распределения размеров в пределах поля рассеяния.

Анализ уравнения (12.1) —кривой нормального распределения — показы­вает, что она симметрична относительно оси ординат (рис. 12.11, а).

'(2л)

(12.4)

При L, = Lcp = 0 кривая имеет мак­симум

S0,4/cr.

На расстоянии ±а от вершины кри­вая имеет две точки перегиба (А и В) С ординатами

УА = УВ = У« = °~{ (2ле)~|/2== = i/maxe-'/2 = 0,6(/max = 0,24/a. (12.5)

Кривая асимптотически приближа­ется к оси абсцисс. Принято считать, что на расстоянии ±3а от вершины кривой ее ветки пересекаются с осью абсцисс, так как при этом 99,73 % всей площади ограничивается кривой. Следо­вательно, отклонения действительных размеров от среднего размера почти для всех обработанных деталей нахо­дятся в пределах от +3сг до —За, т. е. абсолютное значение отклонения равно бег. Если допуск на обработку больше 6f>, то поле рассеяния размеров и погреш­ность обработки меньше допуска, т. е. все детали по размерам годные. Мерой рассеяния (или мерой точности) является среднеквадратическое отклонение а. Оно показывает, насколько тесно сгруппиро­ваны возможные значения действитель­ных размеров обработанных заготовок около центра группирования. Действи­тельно, при увеличении а ордината утм уменьшается [см. формулу (12.1) и рис. 12.11, а], а поле рассеяния м = 6а возрастает, что свидетельствует о мень­шей точности. Чем меньше а, тем незна­чительнее рассеяние размеров и выше точность обработки. Влияние а на форму кривой нормального распределения пока­зано на рис. 12.11, б.

Если при обработке имеются только случайные погрешности, то кривая рас­сеяния принимает симметричную форму.

Рис. 12.11. Кривые нормального распределения

Постоянная систематическая погреш­ность форму кривой не меняет, но ее положение смещается в направлении оси абсцисс. Если построить кривые рас­сеяния размеров, полученных при обра­ботке двух партий заготовок на одном станке, но при двух наладках, то получим две одинаковые кривые (рис. 12.11, в), смещенные по оси абсцисс. Величина AL = L"P — L'Cp характёризует погреш­ность второй наладки станка относи­тельно первой. Аналогичная картина будет наблюдаться, если при разверты­вании отверстий в партии заготовок произошла смена развертки. Таким образом, статистический контроль явля­ется эффективным, средством исследо­вания качества наладки металлорежу­щих станков.

Во избежание брака при обработке необходимо выполнить два условия:

1) пределы рассеяния не должны выходить за поле допуска б размера, т. е. необходимо соблюдать условие 66 <6;

2) центр рассеяния должен быть расположен таким образом, чтобы все размеры детали лежали в пределах допуска.

Выполнение первого условия обеспе­чивается правильным выбором точности станка для заданной работы, второго условия — правильной размерной налад­кой инструмента.

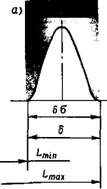
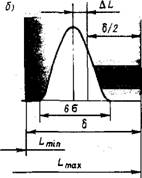
Рассмотрим сначала вопросы, связан­ные с выбором станка по кривым нор­мального распределения (рис. 12.12). На чертеже детали указаны номинальный размер L и допуск. В практике работы возможны следующие три случая.

1. Случай, когда б = 6а (рис. 12.12, а) И центр рассеяния совпадает с серединой поля допуска. Размеры деталей, обра­ботанных на станке, лежат в пределах допуска, брак отсутствует.

2. Случай, когда 6> 6о (рис. 12.12,6), т. е. допуск больше поля рассеяния. Все детали годные, брак отсутствует.

Запас точности ф = 6/(6ст) показы­вает, насколько надежно гарантировано отсутствие брака (при ф> 1,12 процесс обработки считается надежным). Коэф­фициент точности наладки характеризует относительное смещение AL вершины кривой распределения от середины поля допуска: l = AL/Б. Значение AL может быть определено по формуле

AZ. = Z. cp-0,5(/.max + Lmin).

Наладка считается точной, если

/ /дон.

Где /доп допустимое значение коэффи­циента точности наладки:

/до„= (6-6ч)/(26) = (г|>- 1)/(2г|>).

Планировать обработку с большим запасом точности экономически нецеле­сообразно. Точность станка определяет его технологические возможности, точ­ность детали определяет ее сложность. Минимальными затраты на обработку будут в том случае, если технологические возможности оборудования соответст­вуют сложности выполняемой работы.

3. Случай, когда 6<6ст (рис. 12.12, в). Брак неизбежен даже при 1 = 0. Колеба­ния получаемых размеров превышают размеры допуска, и действительные раз­меры некоторых деталей лежат за преде­лами допуска. Можно определить про­цент брака, если взять отношение за­штрихованных площадей к общей площа­ди под кривой распределения. Можно также найти процент исправимого и неис­правимого брака. При обработке валов площадь в правой части кривой распре­деления показывает объем исправимого брака, а в левой — объем неисправи­мого брака.

Рис. 12.12. Выбор станка по кривым нормального распределения

Часть систематических и случайных погрешностей определяется погрешно­стями изготовления самих станков. Неко­торые характеристики геометрической

От способа обработки: 1 — точение; 2 — шлифование

Точности станков общего назначения средних размеров: радиальное биение шпинделей. токарных и фрезерных стан­ков 0,01—0,15 мм; биение конического отверстия в шпинделе токарного и фре­зерного станков (на длине оправки 300 мм) 0,02 мм; прямолинейность и параллельность направляющих токарных ч и продольно-строгальных станков (на длине оправки 1000 мм) 0,02 мм; прямо­линейность продольных направляющих и столов фрезерных станков (на длине оправки 1000 мм) 0,03—0,04 мм.

Приведенные ориентировочные дан­ные относятся к станкам нормальной точности (группы Н). Станки других групп точности имеют меньшие погреш­ности по сравнению со станками нормаль­ной точности: повышенной точности (группа П) — на 60 %; высокой точности (группа В) —на 40%; особо высокой точности (группа А) —на 25%; особо точные (группа С) — на 16 %. Для стан­ков с ЧПУ сохраняются те же группы точности, но исходные нормы точности выше, чем для станков общего назначе­ния, за счет более высокой жесткости станков с ЧПУ.

Все сказанное относится к экономиче­ской точности при работе на налаженном оборудовании. В других случаях законо­мерности могут быть иными. Можно ли на относительно неточном станке до­биться высокой точности? Можно, если рабочий имеет высокую квалификацию и использует специальные технологиче­скую оснастку и инструмент при большой норме времени. Такую точность называют достижимой. Она достижима, но эконо­мически нецелесообразна. Поэтому осо­бенно важен вопрос соответствия техно­логических возможностей оборудования

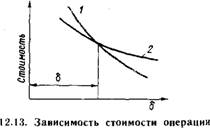
Выполняемой работе. В различных произ­водственных условиях есть границы экономически целесообразной точности. Они зависят от того, существуют ли пригодные для обработки данной детали другие, более точные способы и насколько они экономичны. На рис. 12.13 показаны зависимости стоимости обработки от точности при точении и шлифовании. Деталь с допуском больше 6 выгоднее обрабатывать точением, а с допуском меньше 6 — шлифованием.

Экономическая точность — точность, затраты на которую при данном способе обработки меньше затрат при другом способе обработки. Принято считать, что для токарных и фрезерных станков общего назначения экономически оправ­дана точность обработки по 9—11-му квалитету, а для станков с ЧПУ — по 6—9-му квалитету.

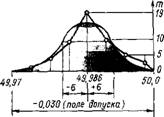
Пример 1. Построение кривых нормаль­ного распределения размеров деталей, обра­ботанных на станке с ЧПУ. Проконтролируем какой-нибудь параметр в партии из 50 дета­лей, например наружный диаметр вала 50_о, оз мм> обточенного на токарном станке с ЧПУ. Разобъем полученные результаты из­мерений значения диаметров на группы с одинаковыми отклонениями в пределах опре­деленного интервала (табл. 12.4 и 12.5).

В рассматриваемом примере размеры разбиты на семь групп через интервалы в 0,004 мм. В табл. 12.5 указаны абсолютная частота M появления размеров внутри каждо­го интервала и частость, равная отношению Ш/N, где N — общее число измерений. Резуль­таты можно изобразить графически кривой распределения. Откладывая по оси абсцисс размеры или отклонения, а по оси ординат — частоту m для каждого интервала размеров (или частость), получим ломаную линию, которая при увеличении числа измерений и числа интервалов будет приближаться к плав­ной кривой (рис. 12.14).

По формуле (12.2) в соответствии с дан­ными табл. 12.5 определим Lcp = 49,986 мм. Среднее арифметическое на графике кривой

Рис. 12.14. Построение кривой распределения размеров обработанных деталей

4S4

Таблица 12.4. Результаты проверки на­ружного диаметра вала, мм Порядковый номер детали Размер, мм Средний размер в группе, мм Порядковый номер детали Размер, мм Средний размер в группе, мм 1 49,977 26 49,984 2 49,975 27 49,986 3 49,980 49,979 28 49,990 49,987 4 49,981 29 49,987 5 49,982 30 49,989 6 49,979 31 49,986 7 49,979 32 49,986 8 49,984 49,982 33 49,989 49,989 9 49,985 34 49,993 10 49,985 35 49,990 И 49,985 36 49,987 12 49,981 37 49,989 13 49,983 49,984 38 49,990 49,990 14 49,987 39 49,991 15 49,983 40 49,995 16 49,987 41 49,992 17 49,984 42 49,988 18 49,988 49,986 43 49,988 49,990 19 49,988 44 49,993 20 49,985 45 49,991 21 49,986 46 49,994 22 49,982 47 49,992 23 49,989 49,986 48 49,997 49,996 24 49,988 49 49,999 25 49,988 50 49,999

Распределения совпадает с центром группиро­вания и почти совпадает с серединой поля допуска 49,985 мм (рис. 12.14).

Среднеквадратическое отклонение нахо­дим по формуле (12.3), пользуясь данными табл. 12.6. Расчет надо вести последовательно по столбцам таблицы. В пятом столбце запи­саны квадраты величин предыдущего столбца, которые для удобства расчета умножены на 106 (практически отклонения в миллиметрах переведены в отклонения в микрометрах). В итоге при суммировании последнего столбца получаем К

X m,(L«-Lcp)2= 1312-Ю-6 ( = 1

Таблица 12.5. Частота т и частость M/N Размеров деталей в партии Интервал размеров, мм Т M/N Св. 49,972 до 49,976 1 0,02 » 49,976 49,980 4 0,08 » 49,980 49,984 9 0,18 » 49,984 49,988 19 0,38 » 49,988 49,992 10 0,20 » 49,992 49,996 5 0,10 » 49,996 50,000 2 0,04

Среднеквадратическое отклонение.. ,

А=([ J m. i(Li— /.,.,,)2 j | '/2 — ;= 1

= [ (1312 ■ 10~6) /50] 1/2 = 0,00512 мм.

Среднеквадратическое отклонение а — единственный параметр, определяющий фор­му кривой нормального распределения, так как остальные члены в уравнении кривой явля­ются постоянными величинами. Чем больше а, тем более растянута кривая, т. е. больше рас­сеяние размеров (см. рис. 12.11). В интер­вале абсцисс х=+3о находится 99,7 % раз­меров всех обрабатываемых деталей. Следо­вательно, если допуск на обработку больше бст, то поле рассеяния размеров и погрешность обработки меньше допуска и все детали ока­жутся годными.

В рассмотренном примере поле рас­сеяния xmax-xmin = 6-0,00512 = 0,031 мм незначительно превышает допуск (0,030 мм). Практически в проверенной партии не встретилось ни одного случая брака, однако, поскольку поле рассеяния превышает допуск, имеется теоретиче­ская вероятность его появления.

Х~хСР, мм (*/■ — Хср) 2106 (Xi — Xcp)2Mi- 106

Таблица 12.6. Данные для расчета среднеквадратического отклонения а Размеры, мм Св. 49,972 до 49,976 49,974 1 — 0,012 + 144 144 » 49,976 » 49,980 49,978 4 — 0,008 + 64 256 » 49,980 » 49,984 49,982 9 — 0,004 + 16 144 » 49,984 » 49,988 49,986 19 0 0 0 » 49,988 » 49,992 49,990 10 + 0,004 + 16 160 » 49,992 » 49,996 49,994 5 + 0,008 + 64 320 » 49,996 » 50,000 49,998 2 + 0,012 + 144 288

Опыт показывает, что кривые распре­деления размеров деталей, обработанных на станках с программным управлением, практически совпадают с кривыми нор­мального распределения. Этот важный вывод позволяет анализировать точность и предвидеть результаты обработки, используя зависимости, установленные

Законом нормального распределения.

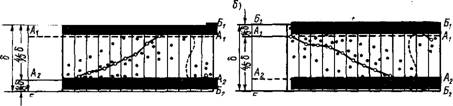
Рис. 12.16. Точечные диаграммы: а — при обработке наружных поверхностей; б — при обработке Внутренних поверхностей;

6 — допуск на размер (поле контрольных границ); линия й, — Б, — верхнее отклонение размера; линия Б2—Б2 — нижнее отклонение; Л2 — уровень наладки при обработке наружных поверхностей; Л, — уровень наладки при обработке внутренних поверхностей; линии At—А,, А^ — Аг — контрольные прямые, характеризующие рассеяние групповых средних размеров обработанных деталей

Вся ограниченная кривой распределе­ния и осью абсцисс площадь определяет в некотором масштабе полное число дета­лей, по результатам измерения которых построена кривая. Часть площади, за­ключенная между ординатами, восста­новленными из точек Х и Х2, кривой распределения и осью абсцисс (на рис. 12.15 заштрихована), соответствует в том же масштабе числу деталей, размеры которых лежат в интервале Х2 — Х1. Вероятность получения деталей в интервале размеров х2—х определя­ется отношением заштрихованной пло­щади ко всей площади, ограниченной кривой распределения и осью абсцисс.