Metallic reflectors, reflective contacts, and transparent contacts
 25 марта, 2014
25 марта, 2014  admin
admin Having been used by humankind for several millenniums, metal-air reflectors are the oldest type of reflector with high reflectivity. Metal reflectors are characterized by a broad spectral reflectivity band and a weak angular dependence of the reflectivity. The first high-quality metallic reflectors were used in reflection telescopes for astronomy applications (Bell, 1922).
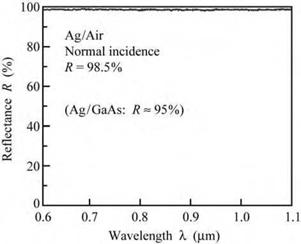
An experimental reflectance spectrum of a silver-air reflector at normal incidence is shown in Fig. 10.2. The reflectance spectrum is characterized by a broad spectral band of high reflectivity and an average reflectance of 98.5%.
|
|
|
Fig. 10.2. Measured reflectance of a silver/air reflector for normal incidence. The average reflectivity in the visible spectrum is 98.5%. |
The reflectance (amplitude reflection coefficient) of a metal reflector and an external medium can be calculated from the Fresnel equation, which for media with complex refractive indices is given by
|
El Ei |
|
2 |
|
(10.1) |
|
r = |
|
2 |
|
N1 + N |
|
N1 - N |
where N1 and N2 are the complex refractive indices of the two media.
The reflected and transmitted intensities are proportional to the square of the electric field. The reflectivity or reflectance (power reflection coefficient) is given by
|
2 |
|
2 |
|
2 |
|
N1 - N |
|
2 |
|
2 |
|
R = |
|
(10.2) |
|
= r |
|
2 |
|
2 |
|
N1 + N |
|
Ei |
|
2 |
|
2 |
|
N1 - N2 |
|
N1 + N |
The energy conservation law requires that the power transmission coefficient in a lossless reflector is given by
|
(10.3) |
T = 1 - R.
Metals are lossy media so that the transmittance T* 0 for thick metal films. The Fresnel equation can be used to calculate the reflectance of a metal-dielectric interface. Assuming that the complex refractive indices of the dielectric and the metal are N1 = n1 and N2 = Щ + i^2, respectively, the reflectance is given by
|
|
|
(10.4) |
ni - n2 + i k2 ,
r = -3 and
n + n2 - i k2
An ideal metal has very high conductivity, i. e. a ^ да and therefore k. (Note that conductivity a and the imaginary part of the refractive index k are related by a = 2 n Ш80 k. Also note that the absorption constant a and the imaginary part of the refractive index are related by a = 4 n k / X0 .) We thus obtain for an ideal metal
|
and |
|
(10.5) |
|
R |
|
1. |
|
1 |
|
r |
|
Фг = n. |
That is, the ideal metal has a unit reflection coefficient, unit reflectance, and a phase shift of n.
Real metals have high conductivity (but not an infinitely high conductivity) and the reflectivity of any real metal is therefore less than unity. Loss mechanisms in metals were first analyzed in terms of the Drude model (Drude, 1904). Table 10.1 gives the n and k values of several metals and semiconductors.
|
Table 10.1. Real and imaginary part of the refractive index for different semiconductors and metals at 0.5 and 1.0 цш.
|
Using Eq. (10.4), the reflectance of a metal-air and metal-semiconductor boundary can be calculated; the results are given in Table 10.2. Inspection of the table reveals that the visible-
spectrum reflectivity is generally lower for metal-semiconductor interfaces than that of metal-air interfaces. This is due to the lower refractive-index contrast of the metal-semiconductor boundary.
|
Material |
R (%) |
|
Al/air (0.5 ^m) |
0.923 |
|
Al/air (1.0 ^m) |
0.955 |
|
Al/GaP (0.5 ^.m) |
0.805 |
|
Al/GaP (1.0 ^.m) |
0.876 |
|
Al/Si (1.0 ^m) |
0.861 |
|
Table 10.2. Calculated reflectivity of metal-air and metal-semiconductor reflectors at 0.5 and 1.0 ^.m. |
|
Material |
R (%) |
|
Ag/air (0.5 ^.m) |
0.982 |
|
Ag/air (1.0 ^.m) |
0.997 |
|
Ag/GaP (0.5 ^.m) |
0.969 |
|
Ag/GaP (1.0 ^.m) |
0.992 |
|
Ag/Si (1.0 ^.m) |
0.991 |
|
Material |
R (%) |
|
Au/air (0.5 ^.m) |
0.514 |
|
Au/air (1.0 ^.m) |
0.979 |
|
Au/GaP (0.5 ^.m) |
0.470 |
|
Au/GaP (1.0 ^.m) |
0.945 |
|
Au/Si (1.0 ^.m) |
0.939 |
Although metals are simple and viable reflectors, the reflection losses or mirror losses are quite high. The loss of one reflection event, (1 - R), is about 5% for metal-semiconductor reflectors. Losses are particularly high for waveguided modes shown in Fig. 10.3. The intensity of waveguided modes decays according to
|
N |
|
(10.6) |
|
1 - NL |
|
I/І0 = RN = (1 - L) |
where N is the number of reflection events, and the mirror loss is L = 1 - R (L << 1.0 and R « 1.0). The equation illustrates that a small difference (e. g. a few percent) in R can make a large difference (e. g. a factor of 2) in the intensity of waveguided modes after N reflection events.
|
|
Metal-semiconductor reflectors have been used in AlGaInP LEDs by Horng et al. (1999a, 1999b) to increase the light-extraction efficiency. The layer sequence of the finished device consisted of AlGaInP/AuBe/SiO2/Si. The p-type AlGalnP-AuBe interface served as a reflector and as a broad-area ohmic contact. The AuBe layer also served as a supply layer for Be acceptors to attain low contact resistance. The contacts were annealed at 450 °C for 15 minutes. The LEDs were fabricated by a wafer-bonding process using a Si substrate. After the bonding process, the
GaAs substrate, on which the epitaxial layers had been grown, was removed. Si has a higher thermal conductivity than GaAs thus allowing for lower junction temperatures and reducing the joule-heating-induced emission-wavelength shift. The emission from the metal-reflector AlGaInP LEDs exceeded those of reference LEDs with DBRs fabricated on GaAs substrates.
Annealing and alloying forms low-resistance ohmic contacts. Typical annealing temperatures for alloyed contacts are between 375 and 450 °C for III-V arsenides and III-V phosphides and up to 600 °C for III-V nitrides. During the annealing process, the metal surface changes from smooth to rough and a concomitant decrease in the optical reflectivity results.
In contrast, non-alloyed contacts are just deposited on the semiconductor without annealing. Highly doped semiconductor surface layers are needed to obtain good ohmic I-V characteristics for such non-alloyed ohmic contacts. However, even for highly doped semiconductors, the contact resistance of non-alloyed contacts is usually higher than for alloyed contacts.
Thick metallic reflectors and hybrid reflectors are absorbing reflectors that should not be used as light-exit reflectors in LEDs and vertical-cavity surface emitting lasers. Metal contacts become practically opaque for thicknesses > 50 nm. That is, the transmittance of hybrid reflectors is near zero, unless the thickness of the metal is very thin (Tu et al., 1990).
Very thin metal contacts are semi-transparent. Most metal contacts have a transmittance of approximately 50% at a metal film thickness of 5-10 nm. The exact value of the transmittance needs to be calculated by taking into account the real and imaginary part of the refractive index (see, for example, Palik, 1998). However, very thin metallic contacts may form an islanded structure rather than a single continuous film. Furthermore, the electrical resistance of thin metal films can be large, in particular if an islanded structure is formed.
In LEDs with transparent substrates, e. g. AlGaInP LEDs on GaP, light emanating from the active region is incident on the substrate contact. To increase the reflectance of the backside, an ohmic contact geometry covering only a small fraction of the substrate surface can be used, such as a multiple-stripe or a ring-shaped contact. Using Ag-loaded conductive epoxy to attach the LED die to the package provides a high-reflectivity material in the regions not covered by the ohmic contact.
The die-attach epoxy can also serve as a reflector in LEDs grown on a transparent material, e. g. GaInN LEDs grown on sapphire substrates. Conductive Ag-loaded epoxy has a high conductivity as well as high reflectance. Such a highly reflective epoxy can increase the extraction efficiency in LEDs grown on transparent substrates.
There are ohmic contacts that are transparent to visible light. Such transparent ohmic
contacts include indium tin oxide, frequently referred to as ITO (Ray et al., 1983; Sheu et al., 1998; Margalith et al., 1999; Mergel et al., 2000; Shin et al., 2001). The material can be considered as a tin oxide semiconductor that is doped with indium. Indium substitutes for tin and therefore acts as an acceptor. Generally the specific contact resistance of ITO contacts is higher than the contact resistance of alloyed metal contacts.

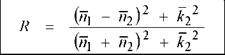

 Опубликовано в
Опубликовано в