МЕРА ИНТЕНСИВНОСТИ ВНУТРЕННЕЙ СИЛЫ
 6 марта, 2013
6 марта, 2013  admin
admin |
М |
Ы уже выяснили, что внутренняя сила складывается из сил взаимодействия бесчисленного множества атомов. Следовательно, по своей природе внутренняя сила есть сила распределённая, подобно силе давления пара на поршень машины.
Но на этом сходство между внутренней силой и давлением кончается. Давление пара на поршень одинаково на любом участке его поверхности. Внутренняя же сила, как
|
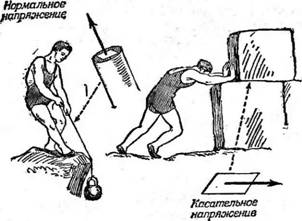
Рис. 4. Нормальные и касательные напряжения. |
Мы увидим в дальнейшем, наоборот, может распределяться по сечению самым различным образом и зависимости от характера деформации (растяжение, кручение, изгиб и др.). Для оценки распределения нпутрепней силы надо иметь меру «плотности распределении», т. е. интенсивности этой силы.
Меру интенсивности внутренней силы шпывают напряжением. Иначе говоря, напряжением насыпается величина внутренней силы, которая приходится па единицу площади сечения.
Как известно, силу можно измерять килограммами, а площадь — квадратными сантиметрами. Поэтому напря- жение измеряется количеством килограммов, распределённых на одном квадратном сантиметре поверхности.
Величину напряжения можно установить на основе знания величины внутренних сил, площади сечения и характера распределения напряжений.
Так же как внешние и внутренние силы, напряжения различаются по величине и направлению.
Напряжение, направленное перпендикулярно к плоскости сечения (под углом 90°), называют нормальным*) напряжением. Если же направление напряжения лежит в плоскости сечения, т. е. угол равен нулю, то напряжение называется касательным. Нормальное напряжение — неразлучный спутник деформации удлинения или укорочения. Касательное напряжение появляется там, где существует деформация сдвига (рис. 4).
Конструктору очень важно знать, какие напряжения возникнут в деталях будущей машины или сооружения от
I I I I
Рис. 5. Деформация растяжения.
Нагрузок, которым подвергнутся эти детали. В нашем примерном расчёте мы установили величину и направление внутренней силы в поперечном сечении каната подъёмного крана (см. рис. 3). Но мы ещё не определили, какие напряжения будет испытывать сталь каната. Для того чтобы узнать это, проделаем простой опыт.'
Возьмём резиновую пластинку и начертим на ней ряд поперечных линий на равных расстояниях (рис. 5). Растянув резину, мы увидим, что расстояния между линиями увеличились, но линии остались поперечными и прямыми, как и прежде. Это означает, что все продольные волокна на поверхности резины удлиняются одинаково. Естественно предположить, что и во внутренних частях пластинки удлинения всех продольных волокон одинаковы. Отсюда следует, что при растяжении внутренняя сила распреде-
*) Слово «нормальный» часто используется математиками вместо слова «перпендикулярный». Значение обоих слов одинаково.
Ляется по поперечному сечению равномерно, т. е. напряжения во всех точках сечения одинаковы. Нетрудно сообразить, что для определения напряжения в этом случае достаточно разделить внутреннюю силу на площадь сечения, т. е. напряжение в поперечном сечении растянутого каната можно определить, пользуясь простой формулой:
Внутренняя сила
Напряжение=--------------------------------------------- .
Площадь поперечного сечения
Предположим, что площадь поперечного сечения каната (см. рис. 3) подъёмного крана 2 см2. Тогда
1000 кг... кг Напряжение = —г - = 500 —.
2 см см2
По своему направлению это напряжение будет нормальным, т. е. перпендикулярным к сечению.
Эта формула помогает определять напряжения в самых разнообразных деталях машин и сооружений, подвергающихся действию растягивающих и сжимающих внутренних сил. Необходимо только иметь в виду, что при сжатии гибкие (длинные и тонкие) детали могут изогнуться, как изогнётся тонкая линейка, если поставить её вертикально и нажать сверху рукой. При возникновении такого изгиба наша формула уже неприменима.
Мы нашли величину напряжения в»поперечном сечении каната. Но эта величина не характеризует ещё прочности каната. Выдержит ли сталь такое напряжение? Может быть, тяжёлая плита окажется для каната непосильной нагрузкой, и он, натянувшись, лопнет, как струна, не успев даже приподнять груз от земли? Может быть, напротив, напряжение 500 кг/см2 далеко не исчерпает возможностей металла, и следовало бы взять канат потоньше, более дешёвый и лёгкий?
Ответы на эти и многие другие вопросы, возникающие перед конструктором при проектировании, даёт знание прочности и некоторых других свойств материалов, из которых будут изготовлены детали машины. Такие сведения получают опытным путём в специальных лабораториях.

 Опубликовано в
Опубликовано в