Уравнения энергии (1.20), (1.21) для каналов постоянного проходного сечения в условиях установившегося теплового режима аппарата примут вид

Л, кг,

Ср1рт-^ = ^02 — Л); (1.24)

Ср2Р2®2 = 5“' (Л — *з)- (1-25)

Учитывая, что С[ = О2 = рг^г^г. <1Р =* 2^х, записываем

Уравнения (1.24), (1.26) в виде

СР|0,Л, = — (1-26)

0,^2 = Ш (/,—/,). (1-27)

6 2

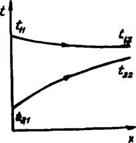
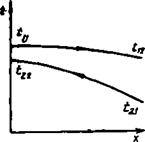
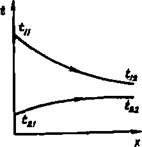
Рис. 1.4. Схема изменения температур по длине теплообменника:

А, 6 — противоток: в, г — прямоток [а. в— срС1 < сря6ш', 6, > СрйО»У

Средняя температурная разность. При определении теплопро - нзводительности теплообменного аппарата введем для ее интег­ральной оценки понятие средней температурной разности: (} = = (1.28). Очевидно, что вся сложность расчета теплопро-

Изводителыюсти аппарата в зависимости от взаимного направления течений теплоносителей переносится на вычисление средней тем­пературной разности ДЛ Рассмотрим простейшую схему течения двух теплоносителей — прямотой (рис. 1.4, а, б). С учетом измене­ния функций температуры /1, /2 перепишем уравнения (1.26),

(1.27) в форме

<Н2 = Срв (-Я0 = ср2С2 (Л2). (1.29)

Оцифровано 11.04.2010

Jank2003@ukr. net 17

Следовательно,

(1.29); *2 = (1-30)

Сс1°1 ср2и 2

Используя уравнения (1.29), (1.30), получаем

"('>-«+ 0-М)

Учитывая, что = Ак#7 (^—/г), а также используя обозначения

“-(5д+*ет)- 4'

Записываем уравнение (1.31) в виде

^1 = —кпиР. (1.32)

Интегрируя последнее вдоль поверхности теплообмена, находим

Г

1т = - Ат1^- О-33)

4<н С

Отметим, ЧТО Д/ изменяется при прямотоке ОТ А(„ = (ц —t2l до Д/« = (12—^22, а площадь — от 0 до А В результате интегрирования получим

1п - ту - = —£/лґ. (1-34)

^ Н

Записав условия баланса количеств тепла первого и второго

Теплоносителей

(з = Ср^І (/ц —Лг) = Сргбг (^22 —^21). (1.35)

Имеем

1 =4-(^11—^12)> — ^21)* (1.36)

Св1®1 <3 ’ сс2°1 С2

Тогда

<3 = кР-н-А, (1.37)

Т = - д - [(/„ — /іг) + (^22 — ^21)] = - ц [Д^н — Д^к]. Подставив уравнение (1.36) в (1.34), найдем

І и |пдГ

■д1

Приравнивая соотношения (1.37), (1.28), получаем

Т7 (і\ ~ *2)~ (ю) /і оо

Рассмотрим схему течения двух теплоносителей — противоток, (рис. 1.4, в, г). Учитывая изменение функций /21 записываем уравнения (1.26), (1.27) в форме

<1С> = с„10, (—Л,) = ср202 (—Л?). (1.39)

Аналогично схеме с прямотоком

= —кт*йР. (1-40)

Здесь

М = — І2‘, т

[сріаі сР202)‘

Интегрируя уравнение (1.40) вдоль поверхности теплообмена, находим

| (1.41)

І*де Д/н = /ц— і22, Д^к = ^12 — ^21 • После интегрирования

1п ^ = —кт*Р. (1-42) Н

Ц д^

Из уравнений теплового баланса теплоносителей определим

Т* = £ [(/»1 - І22) -(<12- <21)1 = £ (Д/в - Д/м).

Тогда

— А<«

= (1-43)

1пЦі

Приравнивая уравнения (1.43), (1.28), получаем средний темпе­ратурный напор при противотоке]

Д<й —Д<„

А 1пдГ

Аі= 6 м

Б (1.44)

При других схемах течения средний температурный напор

, (^11 — ^22) — (^12 — ^21)

? , 'п-*12 ' (1.45)

/_______ у

42 21

Коэффициент ф определяется как функция вспомогательных параметров

При перекрестном токе индексы 21, 22 в соотношениях для Р и R присваиваются среде с меньшей степенью перемешива­ния. В случае параллельно смешанного тока эти индексы присва­иваются среде с меньшим перепадом температур.

Приведем указания по определению температурного напора для некоторых схем взаимного течения теплоносителей. Наибо­лее полно данные по расчету коэффициента 4я рассмотрены в работе [42].

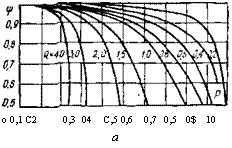
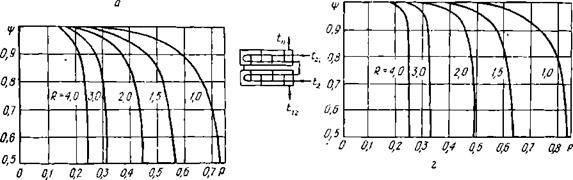
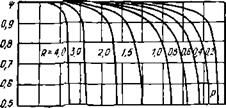
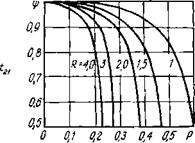
Теплообменники с перекрестным током различаются по усло­виям перемешивания каждой из сред в пределах ходов и между ними. При многократном перекрестном токе должны учиты­ваться число ходов и общая схема взаимного движения — про­тивоток или прямоток, Общий противоток при многократном перекрестном токе соответствует схеме, когда греющая среда встречает сначала последний ход обогреваемой среды, а в кон­це— первый. Общий прямоток — наоборот. Уже при трех ходах коэффициент Ч' для теплообменников с перекрестным током близок к единице, а при числе ходов больше трех поправка не учитывается. На рис. 1.5 даны графики W(P, R) для различных схем перекрестного тока.

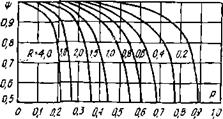
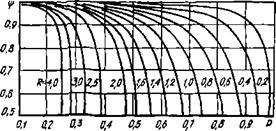
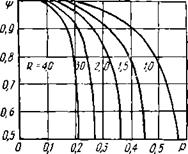
Теплообменники с параллельно смешанным током различа­ются по числу ходов внешней межтрубной среды, по числу хо­дов внутритрубной среды на один ход внешней и по направле­нию движения одной среды относительно другой в пределах одного хода внешней среды. Поправочный коэффициент для теплообменников с одним ходом внешней среды п с любым чет­ным числом ходов внутритрубной принимается таким же, как для теплообменника А (рис. 1.6, а). На рис. 1.6 показаны графики ^(Я, R) для ряда схем параллельно смешанного тока.

Введение понятия средней температурной разности, как бу­дет показано в примерах расчетов теплообменных аппаратов, достаточно эффективно при проектных расчетах (выбор аппа­ратов из стандартного ряда), а также при конструировании новых типов аппаратов.

Конечные температуры теплоносителей. Определение конеч­ных температур теплоносителей на выходе из теплообменного аппарата представляет иитерес при поверочных расчетах ап­паратов, особенно в условиях изменения режимов эксплуата­ции. Поэтому в таких расчетах принимается, что конструктив­ные данные, расходы теплоносителей, начальные температуры и средние по поверхности значения коэффициентов теплопере­дачи известны.

Для прямоточной схемы из уравнения (1.34) определим связь между температурными напорами на входе в аппарат и на выходе из него:

AtK = AtH exp [—kmF]. (1.48)

О 0,1 С2 0,3 04 С,5 0,6 0,7 0,5 0$ 10 А

‘■гг

V

и

'-гг

21

*72

О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Рнс. 1.5. Коэффициент, при однократно перекрестной схеме тока (а — обе среды не пере. мсшиваются; б—обе среды перемешиваются) и при двукратно перекрестном (в — одна среда перемешивается непрерывно, другая только между ходами; г—одна среда перемешивается, другая нет)

Э-

"!Х

=р==р

£

Рис. Г.6. Коэффициент ^ при различных схемах параллсльмо-смешапного тока:

А — теплообменник /—2; 0 — теплообменник 2—2 Л'; о — теплообменник 1—3 с одним прямоточным и двумя противоточными ходами; г теплообменник 4 — 4 {Ы — любое четное число)

)> ------- ^12 -- 2°2 /

СР‘Л

Принимая во внимание, что т = ( с ^

■(22, Д/н = /ц — /21, записываем Л2 = /22 + (/и — *м) ехр

Ср.°1 1 Сс2^2 у]'

*,р

(1.49)

Из уравнения баланса энергии в теплообменнике (1.35) следует Лг = /п —~?1?Г (^22 — /21)• (1.50) Ср|°1 Приравняв уравнения (1.50) и (1.49), найдем ,0, '-гхр[-^г('

Ср1° I Ср2°2

‘-рг Ср2°2

/22 — /21 + (/ц — /21)

(1.51)

1+

Ср2^2

Сд,°' П.

/22 = /21 + (/и — /21)

Ср2^2

Подставив формулу (1.51) в (1.50), после преобразований получим ЬР

Ср|°| Ср2^2

Лг - /11 — (/п — /21) Обозначив П(-

(1.52)

Ср1°1 Ср2°2

1-

-ехр Г________ ^-/1+^1 Ч ср-°. I ^»<?2Л

Ср1С

Л/7

О,/

Ср1°1

1+ ^,01

'о2С1>

Формулы (1.51), (1.52) запишем в компактном виде! /12 = ( —((ц —/21) П;

(1.53) (1.54)

Функцию П ( -, р1^' 1 протабулируем и представим в табл.

Ср1°1 ср2 21

1.1.

Отметим, что современное развитие микрокалькуляторной техники позволяет инженеру легко осуществить анализ влияния основных характеристик теплообменного аппарата на выходные температуры сред и без табулирования функции П.

Для противоточной схемы из уравнения (1.42) определим

Ы = <, + 0п -<*> ехр[-^- (1 -££)} (1.55)

СР,0| ИГ/Гр О,   0.033 0.10 О. эз 0,50 1 2 3 Во   0 0.033 0.10 0.28 0.39 0,63 0,86 0,96 1,00   0.01 0,033 0.10 0,28 0,39 0.63 0,$6 0,96- 0,99   0.05 0,033 0.10 0,28 0,39 0.62 0.84 0,91 ОС5   0.10 0,033 0,16 0.28 0.38 0,61 0.81 0,89 0,91   0.20 0.033 0,10 0,27 0,38 058 0,76 0.81 0,83   0.50 О. оаз 0,10 0,26 0,36 0.52 0,63 0.66 0,67   1,00 0.033 0,09 0,25 0,32 0,43 0.49 0,60 0.50   5.00 0.032 0.08 0.14 0.1$ 0,17 0.17 0,17 0.17   10,00 0.028 0,06 С.09 0,0Й 0,09 0,09 0.09 0.09   20.00 0,024 0,04 0,05 0,05 0.05 0.05 0,05 0,05   50.00 0.016 0,02 0,02 0,02 0.02 0,02 0,02 0,02   100.00 0,09о 0,01 0,01 0,01 0.01 0,01 0,01 0.01

Аналогично тому, как это сделано для прямоточной схемы, по - лучим ^ . с„,в, ?22 = *21 + (/|1 — /21) /'й"

1--^мП~^<Мда] (1.56) Кр Л - ср»С| V ср2°2 1.

?12 - /ц — (^11 — /21)

Ж1У ср2°2 / ]

Р2 2

Обозначив

1 — ехр

Ср1°1

.(1.57)

Ер!°1 Т~7Г СХР Ср2и2

1 —

Ср1°1

! с„ 0 1.1. Значения функции П ---------------------- , —£1— ^рОа

________________ ср1°| ^1^1 ’ Ср 2°2

)-

— :р2°2 / ]

V«?)]

— ехр |^-
	Ср1°1
Ср 1

(1.58) (1.59)

Формулы (1.56), (1.57) запишем в компактном виде: /12 = /ц — (^и —/21) 2;

/22 = /21 + («“и — /21) ~д~ г.

Ср2и2

£>10;				Ы/	СР.0’
'рр1	0.033	1,10	0.33	0.50 |	2	3	Аэ
0	0,033	0,10	0,28	0,39	0,63	0,86	0.95	1.00
0.01	0.033	0,10	0.28	0 39	0,63	0.86	0.95	1.00
0,05	0.033	0,10	0.28	0,39	0.63	0,86	0,94	1.00
0,10	0,033	0,10	0,38	0,39	0.61	0,85	0,94	1,00
0,20	0,033	0,10	0.28	0,38	0,60	0,83	0,93	1,00
0,50	0.033	0,10	0,26	0,36	0,57	0,78	0.89	1,00
1,00	0.033	0,10	0,25	0,34	0,51	0.68	0,77	1,00
5,00	0.033	0.08	0.16	0.18	0,20	0,20	0.20	0,20
10,00	0.028	0,06	0,10	0,10	0,10	0.10	0,10	0.10
20,00	0,024	0,04	0,05	0,05	0.05	0.05	0.05	0,05.
50,00	0,016	0.02	0.02	0,02	0.02	0.02	0,02	0,02
100,00	0,010	0,010	0,010	0,010	0.010	0,010	0,010	0,010

[ кР св 1.2. Значения функции г ------------------ , —й—

с/>,0' срР*

I ^О [ ^ I Функцию г —рт-, ) протабулируем и представим в табл. СШ°1 Ср2и> !

1.2.

Если один из теплоносителей при взаимодействии с поверх­ностью теплообмена изменяет свое агрегатное состояние (кипе­ние или конденсация), то конечную температуру среды, не изменяющей своего агрегатного состояния, определяем по фор­муле

(1.60)

*22 -= — (/< — /21) 6Хр[---------- -~

I С1>2°

С2

(/, — температура насыщения конденсирующегося или кипящего теплоносителя).

Обычно коэффициент теплопередачи неизвестен, и им сле­дует задаться. Точно определять к, не зная конечных темпера­тур теплоносителей, нельзя. Поэтому с требуемой точностью нх можно получить только последовательными приближениями.

Отметим еще одну полезную особенность формул для рас­чета конечных температур теплоносителей. Используя их, можно рассчитывать не только конечные, но и промежуточные темпе­ратуры дли любой точки х, подставляя вместо /7 соответству­ющую величину Ру. Это позволяет построить графики изменения температур рабочих сред вдоль поверхности теплообмена.