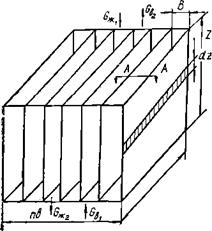
Пленочный ороситель представляет собой систе­му плоскопараллельных каналов, в которых происходит взаимо­действие жидкости, движущейся вниз по оросителю в виде плен­ки, и поднимающегося в противоточном или поперечноточном направлении потока воздуха (рис. 13.1).

Так как толщина пленки жидкости на оросителе может из­меняться по высоте и от ячейки к ячейке, то вводится некоторая средняя по сечению величина — плотность орошения

<7 = Ож/Рор, (13.14)

Где Рау—пЫ — площадь оросителя в плане; п — количество параллельных каналов р оросителе.

Горячая вода поступает на ороситель в количестве СЖ[ с тем­пературой и вытекает в количестве 0Ж2 с температурой (г. Противотоком в градирню поступает влажный воздух с парамет­рами 0ь ср1, Х, I! в количестве 6,1. После оросителя влажный воздух имеет параметры 02, <рг, *2> к-

В пленочном оросителе взаимодействие потоков сопровожда­ется переносом тепла и массы вещества через границу раздела жидкой и газообразной фаз (рис. 13.1,6).

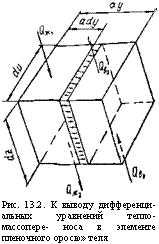
Выделим некоторый элемент объема оросителя высотой йг (рис. 13.2). Ограничимся рассмотрением каналов с одномерным течением жидкости и воздуха в направлении оси г. Количество тепла, внесенное в элемент объема пленки движущейся жидкостью, С? ж1 =сржцси1у(1ли. Количество тепла, вышедшее через противо­положную грань в направлении г, определим по уравнению

С1,к9 = СрЖ (д + ^ с1г^ ^ Ц ас! уёи.

2 t

V'

Lt-W 8, ♦

К

РнЯш 13.1, Схема пленочного оросителя противоточной градирни

Приращение количества тепла в элементе объема пленки .жидкости

DQx = Qy,. — Qm2 = —сРж (я%+ *%)

Количество тепла, внесенное в элемент объема воздуха через нижнюю грань, составляет QB) = срврГ1ш (1—a)dyduQ. Количество тепла, вышедшее через верхнюю грань в направлении г,

Qn2 = ct, BpBffi) (е + ^dz)(l —a) dydu.

Приращение количества тепла в элементе объема движущегося воздуха

<30

DQn = Qr<.;> — О., = cDBpBw (1 — a) dV.

Гак как изменение количества тепла в потоке жидкости должно быть равно изменению количества тепла в потоке воздуха, то

|у)ЛИЧеСТВО жидкости, вошедшее в элемент объема через сечение аДуйи, 6’ж| = qa. dyd. Li. Количество жидкости, проходящее через противоположную грань элемента объема,

Рис. 13.2. К выводу дифференци­альных уравнений тепло-массопере - носа в элементе пленочного оросю» теля

Ож2 = (<7 — д-§г айуёи.

З^тем получим изменение количе­ства жидкости, заключенной в объеме элемента:

=д^а4У

Дг

Изменение количества жидкос­ти, заключенной в элементе объ­ема, согласно закону Дальтона равно количеству вещества, пере­несенному через поверхность йийг й6 >- = Р-' — Р)йийг, тогда

Д£ = Р„,(Р]-Р). (13.16)

Приращение количества тепла в элементе объема пленки жидкос­ти равно сумме количеств

Тепла, перенесенного конвекцией и испарением (массопереносом): д<

С*к/э - = а о(/_0)+г<рро(Я —я).

(13.17;

Перенос жидкости испарением в воздушный поток изменяет ег<? влагосодержание. Запишем количество водяных паров в воз­душном потоке, вошедших в элемент объема через нижнее сече­ние: = рвшх (1—а)йуёи. Количество водяных паров в воздуц>

Но>1 потоке, прошедших через верхнюю грань элемента,

Ож, = р„оу (х + ^ йг (1 —а)йуйи.

Тогда приращение количества водяных паров, заключенных е элементе объема воздушного потока, будет

< >

— С>к. = рвш> ^ (1 — а) йийу.

Так как изменение содержания влаги в воздушном потоке ранено количеству ее, перенесенному испарением через поверх носгь взаимодействия фаз, то

А)йийу^ йг = {Р, — Р) йийг.

(13.18)

Рвви(1 уд2

Используя уравнение (13.8), получаем

Рп (Рб-Р)*‘

$ = 0,622

ДР__ а (Рб ~Р)2(р"________

?вГЮ дг ~~ Рри 0.622Рп

Уравнения (13.15) — (13.17), (13.19) составляют систему отно­сительно переменных я, (, 0, Я в пленочном оросителе для случая ненасыщенного воздуха. Более общая математическая модель пленочного оросителя системы испарительного охлаждения рас­смотрена в работе [13].

К'а° ((— 0);

Если пренебречь изменением плотности орошения жидкости по высоте оросителя и принять Ра — Рб—Рп^сопэ!, то систему уравнений, описывающих изменение состояния теплоносителей по высоте оросителя, запишем в виде

<ю

Ёг

СРВ (Ре“’)

^Р КрРхуРВ Гр'____ <1г (рвш) Р, Г>'

(13.20)

(13.21)

(рн®) йР

(13.22) Значе-

СРЪ (Рвш) аь

& +

'•6|РгЛ, ж<? Лг

При ЭТОМ необходимо иметь В виду, ЧТО р)Л„ = 1,61Рбрр0. ния объемных коэффициентов теплоотдачи а., и массоотдачи рх0 определяются по эмпирическим уравнениям.

Для расчета пленочных оросителей башенных градирен можно

Воспользоваться уравнениями, полученными Л. Д. Берманом [7]:

Р„= 635 (шРв)°'5у)'Э9; (13.23)

А» = 0,29Р*В. (13.24)

Для группы пленочных оросителей вентиляторных и башен­ных градирен рекомендуется уравнение [15]

Б —т

= А

Я-

(13.25)

Значения коэффициентов А, т приведены в табл. 13.2.

13.2. Расчетные коэффициенты оросителей Гип оросителя Высота оросите­ля Ь. м С м-1 ?сух ор м Кор - Ю» и-1 Пленочный — деревян­ные прямоугольные бруски, поставленные на ребро № 1 3.7 0.614 0,223 2,34 0,082 № 2 4,7 0,333 0,513 1,19 | 0,046

Тип оросителя	Высота оросителя И, м	4 и-'		^сух. ор м *	К0Р-ю* м-'
Капельный — деревян­ные прямоугольные бруски № 1	3.7	0,308	0.341	8.92	0,052
№ 2	4.7	0,258	0,399	5.83	0,029
№ 3	3,7	0,265	0,519	5.83	0.029
№ 4	2,7	0,31	0.544	5,83	0,029
Капельно-пленочный № 1	4,7	0.324	0,733	4,64	0,086
№ 2	3,7	0,284	0,532	4.64	0.086
Асбоцементный одно­ярусный с вертикаль­ными волнистым» лнс - •тами и расстояниями между ними № 1 (8 = 15 мм)	2,8	0,468	0,657	6.75	0.049
№ 2 (8 = 25 мм)	2,8	0,441	0,663	4,36	0,037
№ 3 (о = 35 мм)	2,8	0.368	0.518	3.6	0,026
N5 4 (8 = 45 мм)	2,8	0,345	0,527	3,11	0,013

Задача расчета изменения параметров теплоносителей по вы­соте оросителей, описываемая системой обыкновенных диффе­ренциальных уравнений (13.15) — (13.17), (13.19) или (13.20),

(13.21) , может быть реализована на ЭВМ инженерных расчетов типа «Наири-К», «Мир-2». В качестве начальных условий зада­ются следующие: распределение плотности орошения в распре­делительном устройстве (я=яа(х ,у) при г=к0р температура горячей воды задается постоянной ^ = ^2 при г=/г0р. Параметры воздуха задаются относительной влажностью ф = Р/Р" при г = 0.

На участке распределительного устройства принимаются ус­ловия отсутствия тепло - и массообмена с окружающей средой:

А <*Р п.

* = °- = 0 при г = Лор.

Скорость воздуха задается по высоте оросителя: т = №а(г).

Разбив исследуемую область оросителя равношаговой по его высоте сеткой с шагом Дг, можно аппроксимировать систему

Уравнений (13.20) —(13.22) системой алгебраических уравнений относительно сеточных функций 0г, ^ Р(.

Так как в оросителях схема течения противоточная и задан­ными величинами при выбранной высоте оросителя являются тем­пературы горячей воды и воздуха на входе, то, начиная расчет со стороны входа воздуха, необходимо задать температуру воды на выходе. Задача решается для нескольких значений скорости воздуха в оросителе и температур воды на выходе из оросите­ля. Затем строится зависимость температуры воды на входе от скорости воздуха, что позволяет определить необходимую ско­рость, соответствующую температуре горячей воды.

Приняв шЗг по пространственной координате Дг, запишем систему алгебраических уравнений, аппроксимирующих систему

(13.20) —(13.22), разрешенную относительно неизвестных функ­ций 0(> Р„ и

(13.26)

(13.27)

(13.28)

Н,

Где » = 0, 1, 2, 3, .... п, когда п = ~^- Вычислив для исход­ных данных коэффициенты

Сръ(?^)

Р _ СРв(Рв^). р _ МР»«) свжд ' 11 ШРвсржЯ

И задав значения £0> ®о, Ро последовательно для каждого значе­ния »-го шага по высоте оросителя, вычислим распределения температуры воды (с, температуры воздуха 0( и парциального давления водяного пара Р* по высоте оросителя (» = 1,2, ., п).

Как видно, система алгебраических уравнений (13.26)—(13.27) может быть легко разрешена с помощью микрокалькулятора.

Математическая модель пленочного оросителя, описанная системой уравнений (13.20) — (13.22)-или более точной системой

(13.15)— (13.17), (13.19), позволяет при заданной плотности орошения, температуре и относительной влажности воздуха на входе в ороситель выбрать необходимую скорость воздуха и вы­соту оросителя, обеспечивающих заданный уровень охлаждения жидкости в градирне. По найденным скорости воздуха, плот­ности орошения, гидравлическому сопротивлению оросителя
можно выбрать необходимое аэродинамическое вытяжное устройство.

Значение тяги башенной градирни определяется разностью статических напоров внутри башни и вне ее, тогда можно записать

Г = (Ht + 0,5/iOp) (рв, — рп2) g, (13.29)

Где Не — высота вытяжной башни от верха оросителя, м; Лор — высота оросителя, м; рн!, pU2 — плотности воздуха на входе в оросительное устройство и на выходе из него, кг/м3.

Определим потерю напора на преодоление гидравлических сопротивлений градирни:

Г'-Еовщ-^, (13.30)

Рв1 + Рв2 Pep g >

Где Еобщ — коэффициент гидравлического сопротивления течения воздуха в градирне; w — скорость воздушного потока в ороси­теле. Решая совместно уравнения (13.29) и (13.30), находим ско­рость воздушного потока в оросителе при выбранных конструк­тивных параметрах /i„p, ;0сщ, #6-

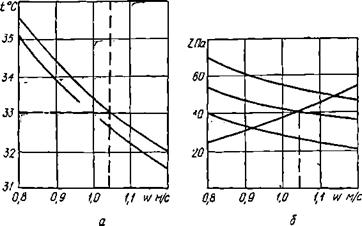
Чтобы по заданным условиям работы оросителя, температуре горячей воды на входе в ороситель t, параметрам воздуха ©i и фЬ плотности орошения q решить проблему выбора оптималь­ной скорости w, целесообразно использовать графоаналитиче­ский метод. Построив на графике семейство характеристик г(Нб), характеристику г' и кривые изменения температуры воды на входе в ороситель, полученной в результате решения системы уравнений (13.26) — (13.28), а также кривую изменения температуры воды на выходе из оросителя по значениям i2, за­данным в расчетах (рис. 13.3), определим необходимые Яб и w. Если окажется, что температура воды на выходе не соответ­ствует заданию, необходимо изменить высоту оросителя hop.

Пример. Определить скорость движения воздуха в пленочном оросителе высотой hop = 2,5 м при начальной температуре воздуха 0о = 26,5 °С и относн- 13.3. Сводные данные о коэффициентах теплоотдачи, массоогдачи и коэффициентах уравнений (13.26)—(13.28) Z 1 СИ О. Т М/с *? Аи Вт/(м* К) Pxv *г/м8 4 Я О В 1 0.« U,95 0.95 550 2200 0,163 0.150 0,112 1,744 2 1.U 0,95 0,95 640 2560 0,150 0,138 0,141 2,188 3 1.2 0,95 0,95 710 2840 0,138 0,128 0,168 2,617

Рис. 13,3. Определение скорости воздуха п оросительном устройстве башенных градирен Пуск )

	ГА2—1---------- . Печать
	Результатов

Вбод исходны* данных

Г Вычисление Шикт,

-АН

©

Га.

‘ание Рп ПП-ИП

©

(0стано6~*)

Бычисшше козсрфициетт уравнения 03261-(Я 23)

Щ>

Иие' 'р>>~

ПП-ИП

Расчет Функций и. Ви Р;

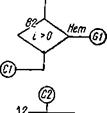
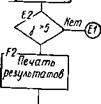
Рис, 13.4. Блок-схема программы расчета испарительного охлаждения на плв* ночном оросителе

26.5 27.96 27.35 30.68 31,9-1 33.14 34.20 35.37 36.41 37.41 38.37

35.5 36,52 37,49 38.42 •39,31 40,16 40.98 41.78 42,65 43.31 44.05

0,00 0.26 0.50 0,75 1,00 1.25 1.50 1,75 2,00 2.25 2.50

0 1 2 3 4 5 6 7 3 9 10

1.46 27,96 5.767 3,453 2,473 0.493 2,967 0,16 0,86 36.52 1,39 29,35 6,098 3.761 2,967 0.469 3,437 0,15 0,82 37.40 1.33 30,68 6,428 4,076 3,437 0,463 3,900 0.15 0,78 38,42 1,26 31,94 6,760 4,385 3,900 0,428 4,328 0,14 0,75 39,41 1,20 33,14 7.092 4,719 4.328 0,415 4,743 Олз 0,72 40,16 1.14 34,28 7,420 5.063 4.743 0,402 5.144 0,12 0,70 40,98 1.09 35.37 7,751 5,380 5,144 0,391 5,535 0,12 0,68 41.78 1.04 36.41 8,086 5.726 5.535 0,383 5.920 0 И 0,66 42.55 1.00 37,41 8,418 6,086 5.920 0,375 6,295 041 0,65 43.31 0.96 38,37 8.758 6,401 6,295 0,369 6,634 0,10 0,64 44,05 ___ — 9,101 6,742 6,634 — —

Режим

Р/+1 КПа

+ АГ

+

С

°с

О. Ч

+

А •-» О.

9 8,56 8.14 7,74 7.37 7,02 6,70 6,41 6.14 5,90

Режим II 0 0,00 33,36 26.5 6,86 1,03 27.53 5,121 3,453 2,474 0,364 2,838 0,14 0,80 1 0,25 34.30 27,53 6,77 1,02 28,55 5.396 3,669 2.838 0,350 3,195 0,14 0,77 2 0,50 35,21 28,55 6,66 1,00 29,55 5.674 3,891 3,195 0.350 3,538 0,14 0.75 3 0,75 36,10 29,55 6,55 0,98 30,53 5.960 4,124 3.538 0.334 3.872 0,13 0,77 4 1,00 36,96 30.53 6,43 0.96 31,49 6,247 4,364 3.872 0.327 4.199 0,13 0,72

34.30 35.21 36.10 36.96 37.81

(	Г	Зс	9, - С	И О 1	И 0 А 1 Ч	9 +	СО С * * С* а.	«9 С * & СО й.	Та С А! V	V 1 * хГ* ^ ■ С Щ а	Рж КПа	± А- Ч Р	1 У + £,*£■ 1	*1+1 °с
5	1,25	37,81	31,49	6.32	0,95	32,44	6.541	4,587	4.199	0,324	4.523	0,13	0.72	38,62
6	1,50	38,61	32,64	6.21	0,93	33,26	6,844	4,862	4.523	0.322	—	0.13	0,71	39,46
7	1,75	39.46	33,36	6,10	0,92	34,28			—	—	5,163	0,13	0.70	40.29
8	2,00	40,30	34.28	6,02	0,90	35,18	7,476	5,390	5,163	0.320	5,482	0,12	0.69	41,11
9	2,25	41.11	35,18	5,93	0,89	36.07	7,804	5,666	5.482	0.320	5.803	0.12	0.69	41.92
10	2,50	41,92	36,07				8.145	5,933	5.803	—	—	—	—	—

Режим III 0 0,00 31,96 26,5 5,64 0,75 27.25 4.732 3,453 2.474 0.289 2.762 0.12 0,75 32,83 1 0.25 32,83 27,25 5,58 0,77 28,02 4.970 3,608 2.762 0,282 3,038 0,13 0.74 33.70 2 0,50 33,70 28,02 5.63 0,78 28,80 5,220 3.774 3,038 0,278 3,310 0,13 0,73 34,56 3 0,75 34,56 28,80 5,76 0,79 29.59 5,474 3.950 3,310 0.275 3,598 0,13 0.72 35.41 4 1,00 25,41 29,59 5,82 0,80 30,39 5,738 4,137 3,598 0,277 3,874 0,13 0,72 36.26 5 1.25 36,26 30.39 5,87 0,81 31,20 6,011 4.328 3.874 0.274 4,148 0,13 0,72 37.10 6 1,50 37,10 31.20 5,90 0,81 32,01 6.294 4,533 4,148 0.274 4.422 0.13 0,72 37.95 7 1,75 37.95 32,01 5,84 0,82 32,83 6,590 4,756 4,422 0,277 4.700 0,13 0,72 38.80 8 2,00 38,80 32,83 5,97 0,82 33.65 6,900 4.970 4,700 0,882 4,991 0,13 0,72 39.66 9 2,25 39,65 33,65 6,00 0,83 34,48 7.219 5,210 4,991 0,285 5.268 0.13 0,72 40,50 10 2.50 40,50 34,48 — — — 7,573 5.450 5,258 — — — —

Тельной влажности у — 72 %. Плотность, орошения <7 = 7,18 мэ/мг • ч. Темпе­ратура горячей воды = 41,6 °С.

Рассмотрим одноярусное оросительное устройство из плоских асбоцементных щитов с расстоянием в свету Ь = 25 мм. Согласно данным Всесоюзного науч­но-исследовательского института гидродинамики им. Б. Е. Веденеева в этом случае применимы уравнения тепло-и массообмена (13.23), (13.24). Так как скорость воздуха ь оросителе неизвестна, расчеты выполняются для трех про­извольно заданных значений скорости и трех значений температуры на выходе из оросителя, чтобы иметь возможность построить график зависимости темпе­ратуры воды от скорости воздуха в оросителе.

Математическая модель переноса тепла и массы в пленочном оросителе ап­проксимируется системой уравнений (13.26) — (13.28) для сеточных функций

0С, Р(. Примем шаг разбивки области сеткой по координате г равным Дг — = 0,25 м.

Расчеты выполним для следующих исходных данных:

1 — <7 = 7,18 м3/м* ■ ч, 60 = 26,5 °С, <р0 = 72 %, ш = 0,8 м/с, 12 = 35,5 °С;

2 - <7 = 7,18 м3/м2 • ч, 60 = 26,5 °С, ?0 = 72 %, ш = 1 м/с, 12 = 33,4 °С;

3 — Я = 7,18 м3/м2 • ч, 60 = 26,5 °С; <р0 = 72 %, ни = 1,2. м/ /2 = 32 СС.

Результаты предварительных расчетов представлены в табл. 13.3, 13.4. Для определения параметров Р( , Р используем табл. 13.1.

Для аппроксимирующей системы дифференциальных уравне­ний разностной алгебраической системы (13.26) — (13.28), урав­нений естественной тяги в башне (13.29) и гидравлического сопротивления градирни (13.30) составим программу расчета параметров потока жидкости, влажного воздуха и выбора 'вы­соты башни, обеспечивающих охлаждение воды от температу­ры /г до заданного уровня. Предлагаемая программа составлена на языке АП (табл. 13.5) для машин типа «НАИРИ-К».

Подготовка исходных данных и расчет выполнены для рас­смотренного ранее примера. Табулирование функции рп = /(о) и Я" = /(/) взяты из табл. 13.1. Блок-схема программы расчета представлена на рис. 13.4.

13.5. Идентификаторы программы Физические переменные Переменные на языке АП Физические переменны Переменные на языке АП Лор Ф. И (п А О • ■* 1 Ц Рв; Пк Дг ^общ *0 РЫ V Рв Рв Ип Рж °2 Р" (<с) И,

Физические переменные	Переменные на языке АП	Физические переменные	Переменные на языке АП
Rt	Fl3	/>” (0,)
(Яб + 0.5Яор)ё	А4	Pt	Pi
Vi	Ш/А	А ?xv	Н/
Ь	Clk	Av	Е/
Wj	Sjk	(Рв, - Р„) (Яб+ - y/!°p)g	Mi
«i		Общ	Ы,

Программа расчета параметров жидкости, влажного воздуха и высоты башни

|' = 5* = 2icr4 | = 5 I =

=• И I t и

/=»Бнетым£=12вбя/>о

Яду

1. Введем ф Ц

2. Допустим £ = О

3. Введем а(

4. Вставим £ = £ + 1

5. Если t — б < 0 идти к 3

6. Допустим j = 0 k = О

7. Введем s/fe cjk rjk 4ik uijk

8. Вставим / = / + 1

9. Если j — 5 < 0 идти к 7

10. Допустим / = 0 £=0

11. Введем 1ц tjt

12. Вставим / = j + 1

13. Если j — 5 < 0 идти к 11

14. Допустим £ = 0

15. Введем ог - xt Д; у;

16. Вставим £ = 1 + 1

17. Если t — 11 <0 идти к 15

18. Допустим / = 0

19. Допустим £ = 0

20. Допустим й = £;Ч

21. Программа ип (oll X йг)

22. Если £ — 10=0 идти к 40

23. Вычислим н f«=635exp(0,59 ln(s/Az) X X exp (0,39 ln clk) e j = 0,29 и(. uЯ= = 2

.24, Вычислим ь5 = e^/(fl[ZS/Au)

= (н/ч/*Ф)/(4/*г/й цг)

А? = (a2c/A)

Я8= (e32s/*V (1 <61<22^/fe4/*)

25. Допустим ж= и = I

26. Программа и« (д 11 у ж г)

27. Если п — 1 > 0 идти к 32

28. Допустим в(. = г

29. Вставим п = я+ 1

30. Допустим ж =

31. Идти к 26

32. Допустим б^ = г

3?. Если £ > 0 идти к 39

34. Вычислим м] = + а5(< .(—,

М2 = аб(В1 — ш/*б,) + ш/йб£ м3 = а7(м, - £,7) + а8(м2 -

-ш Цбд+*Ц

35. Вставим £ = £ + 1

36. Допустим м, = м3 р(. =

=

37. Печатаем с 3 знаками £?.( 1^р1

38. Идти к 25

39. Вычислим м, = 1^ + о5

М2 = аб (в< — ш/*б0 + Р(

М3 = а1 (м, - 1Н) + а8 (м2 - р,)+

+ 1а

40. Вставим £ = £ + 1

41. Допустим = м, = м3 р, =

= м2

42. Печатаем с 3 знаками <др£

43. Если £ — 10 < 0 идти к 25

44. Допустим £ = 0

45. Вычислим я9 = а4 иц аю = = а0«^/ч

46. TOC o "1-5" h z Допустим I = 10 50. Печатаем с 3 знаками с;Л т/

47 ’ Допустим й = 1^ ы

48. Идти к 21 51. вставка ;'= /+ 1

49. Вычислим а,, = а0г/ч т^ад— 52. Если ;—5 < 0 идти к 19

— а, г

53. Кончаем

4 , 54. Исполним 1

, = (0|Р + ам)

В рассматриваемом примере массивы исходных данных при температуре 25 °С

Иб = 70 а, = ср в = 1,0053 кДж/кг

Лор = 2,5 м а2 — срж = 4,179 кДж/кг

Дг = 0,25 а3 = г. = 2442 кДж/кг

«с = ^общ = 85 Ч = (но + °-5/1ор) в = 698,96 м2/ о2

*/* =ш/ ск = Я, ■> = РЫ

А.’10 = 0,8 м/е <710 = 7,18 м3/м2 • ч Рб0 = 100 кПа

Юл = 1,0 м/о = 7,18 м8/ма • ч Рб1 = 100 кПа

Ш,2 = 1,2 м/с 912 с= 7,18 ма/м2 > ч Рб2 = 100 кПа

Ш]3 = 1,3 <?|з = 7,18 м8/м3 • ч Рвз = 100 кПа

Сим=1,4м/с?14 = 7,18 мэ/м* • ч РС4 = 100 кПа

= = 6/о гуо='/о

Рв0 = 97,53 кПа = 0,72 0ОО = 26,6 °С t00 = 35,5 еС

Ри1 = 97,53 кПа = 0,72 6,0 = 26,5 вС tl0 = 33,36

РГ12 = 97,53 кПа?2 = 0,72 в20 = 26,5 /30= 31,96

Рс3 = 97,53 кПа ь = 0,72 0ЗО = 26,5 9С г30 = 30,06

РБ4 = 97,53 кПа <р4 = 0,72 04О = 26,5 ?40 = 30,3 *>С

Массив интерполируемых функций Р" = /(/) рг = г (в)

Ы

Ог = '	*/= Рв	Ес = ' У,-	= Р"
О0 = 25	Х0 = 1,185	«о = 25 Уо	= 3,16
О, = 27	= 1,177	«1=27 у,	= 3,56
О2 29	*2 = 1,169	82 = 29 у2	= 4,00
°з = 31	*3 = 1,161	«з = 31	Уз = 4,48
О4 = 33	*4 = 1,154	«4 = зз	У4 = 5,02
°5 = 35	*5= 1,146	«я = 35	У5 = 5,61
°в = 37	*6 = 1,139	«6 “37	Уб -= 6-26
О7= 39	Х7 = 1,132	«7-39	У7 “ 6,97
°8= 41	*8 “ 1,124	$8 = 41	У8 = 7176
°в	*9= 1,117	«9 = 43	У9 = 8,62
»10=45	*10 = ‘»ПО	«10 = 46	Ую = 9»56