МАГНИТНЫЕ СИСТЕМЫ МАГНИТОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ И ЭЛЕМЕНТЫ ИХ ПРОЕКТИРОВАНИЯ
 19 марта, 2014
19 марта, 2014  Mihail Maikl
Mihail Maikl Одним из основных элементов магнитометрических преобразователей является магнитная система, обеспечивающая представление контролируемого параметра (тока, угла) в виде напряженности поля. Характер распределения напряженности по объему датчика существенно влияет на основные характеристики преобразователя.
В протонно-прецессионном преобразователе неоднородность магнитного поля, как показано в § 1-2, приводні к резкому увеличению скорости затухания сигнала прецессии, оказывая на ядерную систему действие, во многом аналогичное увеличению спин-спиновой релаксации или уменьшению постоянной Т2, так как из-за различающейся напряженности спиновые моменты каждого из сечений датчика прецессируют на различной частоте. Это сопровождается увеличением скорости расфазировки ядерных моментов.
В самогенерирующих квантовых преобразователях (мазерах) влияние неоднородности магнитного поля в связи с зависимостью частоты от поля {см. (1-51)] сводится к уширению резонансной линии и снижению амплитуды автоколебаний. Причина уширения линии та же, т. е. спиновые моменты камеры поглощения прецессируют в различном поле на разной частоте. В связи с этим в формировании сигнала в цепи обратной связи начинает принимать меньшее количество частиц, частота которых близка к пиковой частоте линий, уменьшается амплитуда выходного сигнала и снижается отношение сигнал/шум.
Уширение резонансной линии из-за снижения добротности осциллятора приводит к увеличению степени влияния возмущений. Это снижает и порог чувствительности преобразователя, так как минимальное поле, которое можно преобразовать, примерно равно половине ширины линии. Поэтому разработка требований к магнитным системам преобразователей с точки зрения обеспечения заданной точности и анализ способов получения необходимой однородности поля в объеме их датчиков являются одними из основных задач при прецизионном преобразовании электрических параметров и угловых перемещений в код.
Для того чтобы наилучшим образом выбрать конструкцию и размеры магнитной системы, необходимо установить зависимость величин, характеризующих степень неоднородности магнитного поля от параметров магнитной системы. Степенью неоднородности может служить наибольшая абсолютная величина разности АЯ0бр между значениями напряженности поля в центре образца Но и в наиболее удаленной его точке х.
Для магнитных систем, обладающих осью симметрии и перпендикулярной к ней плоскостью симметрии, это означает, что
где Нх — аксиальная компонента поля на границе образца.
Из закономерностей, проанализированных в § 1-2, вытекает одно из основных требований к магнитным системам протонно-прецес - сионных преобразователей, состоящее в том, что неоднородность поля, создаваемого магнитной системой, не должна приводить за время измерения Гизм к модуляции сигнала прецессии, которая понизила бы отношение амплитуды сигиала к амплитуде шума до величины меньшей, чем требуется для обеспечения заданной точности контроля параметров бт. т.
Тогда величина допустимого уменьшения значения отношения сигнал/шум А и может быть определена из соотношения [50]
|
|
где Я к — напряженность поля, пропорциональная контролируемому параметру.
Для проверки выполнения соотношения (4-4) необходимо вычислить форму огибающей сигнала и найти его изменение за время измерения.
Функция распределения неоднородности поля может быть определена аналитически, экспериментально или получена методами математического моделирования.
В качестве исходных параметров при разработке требований к магнитным системам квантовых преобразователей могут быть взяты такие ограничения, как чувствительность, габариты, предельное значение тока преобразователя и др.
Например, при заданном значении чувствительности и выбранном рабочем веществе датчика может быть определено первое приближение для постоянной магнитной системы по формуле (2-41), а при наличии ограничений на габариты и предельное значение тока
можно осуществить выбор ее геометрии, определить число витков и запаздывание преобразователя.
Расчет поля в объеме камеры поглощения позволит найти максимальную неоднородность и вызванное ею уширение резонансной линии, сопоставление которой с требуемым значением порога чувствительности позволит сделать предварительное заключение о правильности выбора магнитной системы квантового преобразователя.
|
У |
|
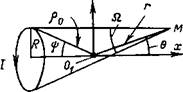
Рис. 4-15. К расчету напряженности магнитного поля, создаваемого в точке М круговым контуром. |
Учитывая особенности конструкции преобразователей, основанных на магнитометрических принципах, к их магнитным системам предъявляются также другие требования, которые, в частности, должны обеспечивать:
возможность выполнения многообмоточных систем, что является необходимым условием создания многоканальных частотных преобразователей;
минимум дополнительной погрешности, связанной с изменением геометрических размеров и сопротивлений обмоток при колебаниях температуры окружающей среды или при обтекании их контролируемым током;
минимум динамических погрешностей, зависящих от постоянной времени нарастания тока в обмотках магнитной системы;
максимальную помехоустойчивость и помехозащищенность от воздействия внешних. магнитных полей;
возможность размещения в центральной области протонно-прецессионного или квантового датчиков с требуемым объемом рабочего вещества;
минимальные габариты, что может являться в ряде случаев необходимым условием использования магнитометрических преобразователей.
Из рассмотрения требований к магнитным системам протоннопрецессионных и квантовых преобразователей становится очевидным, что практический интерес представляют лишь те системы, которые обеспечивают напряженность поля на длине образца, весьма мало отличающуюся от напряженности в центре.
Для создания магнитных полей с высокой однородностью используются различные магнитные системы. Если известно размещение проводников в контуре, то напряженность магнитного поля в каждой точке пространства может быть точно вычислена и, если не считать влияния внешних полей рассеяния, может быть достигнута любая желаемая степень неоднородности.
Вычисление телесного угла Q приводит к следующему выражению для магнитного потенциала в точке М [Л. 71]:
1 _ cos ф _ Sin= Ф 4" (_pr)”X
гдеРп(соз'ф) и Рп (cos 0)—полиномы Лежандра; г — полярное расстояние точки М от начала координат 04.
В полученных формулах для напряженности поля кругового контура предполагалось, что ток протекает'по бесконечно тонкому проводу. Однако на практике обмотка занимает некоторый объем, что уменьшает мощность, рассеиваемую в единице объема. Кроме того, однородность магнитного поля, созданного одиночной катушкой, невелика. Поэтому чаще применяют катушки более сложного типа.
Для получения в небольшом объеме магнитного поля высокой однородности часто используются кольца Гельмгольца, которые, как известно, представляют собой два круговых контура одинакового диаметра, расположенные параллельно друг другу на расстоянии L=R и имеющие центры на общей оси. Практически в такой магнитной системе вместо одного витка используются однослойные или многослойные обмотки, имеющие w витков. Однослойные катушки, вследствие малого количества витков, создают слабую напряженность магнитного поля. Многослойные катушки, создавая более сильное поле, обеспечивают более низкую точность расчета поля из-за значительной погрешности определения диаметра и расстояния между катушками.
Изменение температуры также сильно влияет на геометрические размеры катушек. Например, при изготовлении их из силумина изменение температуры на 1°С вызывает относительное изменение радиуса на 10~5. Даже если при этом компенсируется. соответствующее изменение сопротивления, напряженность поля согласно (4-11) изменится на величину того же порядка.
Преимущество магнитной системы, состоящей из колец Гельмгольца, перед другими системами заключается в доступности пространства, в котором создается равномерное поле.
При проектировании магнитных систем для ядерных преобразователей допустимая степень неоднородности магнитного поля в объеме датчиков может колебаться в значительных пределах в зависимости от метода возбуждения прецессии и требуемой точности преобразования параметров. По этой причине целесообразно рассмотреть характер изменения напряженности поля, создаваемого парой катушек, и способы повышения его однородности при заданных габаритах колец Гельмгольца. Наибольшая протяженность области однородного поля получается в том случае, когда разность между относительным изменением напряженности поля и величиной поля в средней плоскости как раз соответствует допустимой величине отклонения поля от однородного.
Протяженность области, в пределах которой относительное изменение напряженности поля оказывается заключенным между своим максимально допустимым значением и ее значением в центральной части, может быть определена как оптимальная длина.
На рис. 4-16 приведены результаты расчета по формуле (4-10) относительного изменения напряженности поля по оси колец Гельмгольца простейшего типа с числом витков w— 1 при изменении расстояния между катушками от R до 1,1 R через 0,01 R и от 1,1 R до 2R через 0,1 R[12]. Из этих данных следует, что при небольшой величине допуску на неоднородность поля, например для протЪнно-пре - цессионных преобразователей, следует тщательно подбирать расстояние между катушками, так как характер распределения поля очень чувствителен к расстоянию между катушками.
В ряде работ (Л. 23, 61] предлагаются магнитные системы с большим, чем у обычных колец Гельмгольца, числом контуров,
|
Рис. 4-16. Изменение напряженности при нарушении условия L=R. |
обеспечивающие заданную степень неоднородности в том же объеме, но при меньших габаритах магнитной системы. Однако многоконтурные системы имеют ряд недостатков, связанных со значительным усложнением конструкции магнитной системы, необходимостью ее тщательной юстировки и уменьшением рабочего пространства.
В качестве магнитных систем преобразователей могут быть использованы также миниатюрные соленоиды.
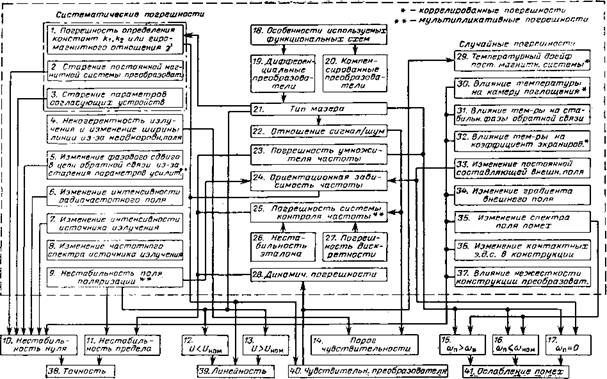
Особенности магнитометрических преобразователей определяются также их функциональными схемами и условиями применения. На рис. 4-17 приведена классификация погрешностей магнитометрических преобразователей типа аналог—код и показана взаимосвязь отдельных составляющих ошибок. Систематические погрешности выделены в отдельную группу (поз. 1—9). Основную часть этих
|
Рис. 4-17. Классификация погрешностей магнитометричеошх преобразователей типа аналог—код и их взаимосвязь с обобщенными характеристиками точности. |
погрешностей представляют методические ошибки (поз. 1—7). Случайные погрешности связаны главным образом с изменением температуры окружающей среды, внешнего магнитного поля и изменениями углового положения магнитных контуров преобразователя из-за конечной жесткости конструкции (поз. 29—37).
Погрешности проявляются по-разному в зависимости от типа функциональной схемы, типа датчика, рабочего вещества мазера (поз. 18—22). Особый класс погрешностей представляют динамические ошибки, связанные с изменениями контролируемых параметров во времени. По физической природе ошибок они могут быть отнесены к методическим, так как определяются постоянной Т2, т. е. инерционностью спиновой системы, и в меньшей степени — магнитной системы, а по причинности вызывающих их возмущений — к случайным. Так же обстоит дело с ориентационной зависимостью частоты (см. § 1-4) и погрешностью умножителя частоты (поз. 23, 24), используемого в низкочастотном гелиевом мазере (на Не3), параметры которого приведены в табл. 1-2; поэтому в классификации динамические погрешности занимают промежуточное положение.
В приведенной классификации отражено наличие связей между отдельными возмущениями, которые вытекают из особенностей разработанных выше функциональных схем и физических процессов в преобразователях (рассмотренных в § 1-2—1-4). Эти связи определяют обобщенные метрологические характеристики точности: нестабильность нуля преобразователей;
* . линейность выходной характеристики преобразователей и стабильность ее крутизны;
чувствительность к изменениям входного сигнала; степень ослабления помех.
Для исследования взаимосвязи этих характеристик с ошибками первого и второго рода (11) необходимо знание закона распределения нестабильности передела, под которым понимается закон распределения погрешностей при контролируемом сигнале, близком к предельному значению. Эта характеристика также является обобщенной— она формируется из оценок типа чувствительность, степень ослабления помех и линейность.
В качестве примера для иллюстрации связей между ошибками можно указать, что нестабильность нуля преобразователя протоннопрецессионного типа определяется степенью старения параметров его магнитной системы сгG и согласующих устройств сгд, а нестабильность нуля квантовых преобразователей находится с учетом основных коррелированных составляющих (поз. 29,30 и 32) по формуле:
ао = "Ь q2R "Ь а0.с"Ьас “Ь аи "Ь а34“На29~Ьазо + Ззг)2»
где (То. с — сдвиг частоты мазера из-за влияния изменения фазы в цепи обратной связи; сгс — сдвиг частоты из-за изменения интенсивности сигнала в цепи обратной связи мазера; сги — сдвиг частоты из-за изменения интенсивности источника излучения.
Нестабильность нуля квантовых преобразователей дифференци ального типа для временного интервала непрерывной работы порядка 100 ч (исходя из достигнутой в неподвижных квантовых градиентометрах длительной "стабильности нуля и возможной степени компенсации магнитных помех типа вариации градиента поля с помощью экрана) может быть около 0,001 % предельного значения приращения поля и лучше. Нестабильность возрастает с ухудшением степени демпфирования помех и качества термостатирования датчика. Предельное значение полезного приращения поля целесообразно из-за снижения линейности ограничить величиной 5 000— 10 ООО гамм.
Под нестабильностью предела понимается вероятный разброс результатов преобразования, получаемых непосредственно после калибровки мазера, исключающей уход его от нуля. хМетодика калибровки рассмотрена в § 4-2 и состоит в использовании режима синхронизации мазеров с целью возможно более точной оценки наличия разности частот при отсутствии сигнала.
Линейность различных вариантов преобразователей зависит в основном от типа рабочего вещества, наличия квадратичного члена в выражении для частоты и качества усилителя. В соответствии с рис. 4-17 линейность находится для двух случаев преобразования— на номинальной шкале (U=UEом) и при перегрузках по входу (£/>£/ном), которые имеют место в режиме автоматического поиска шкалы. Количественные характеристики линейности зависят от диапазона входных сигналов (см. § 1-4).
Нелинейность выходной характеристики преобразователя с цезиевым мазером при точности преобразования на уровне 0,01 — 0,005% можно не учитывать. ’
Повышение чувствительности можно производить за счет увеличения постоянной магнитной системы. Однако при уменьшении габаритов последних до 10—12 см из-за возрастания неоднородности поля и снижения отношения сигнал/шум, ниже допустимого соотношением (4-4) уровня, в обычной магнитной системе типа колец Гельмгольца пока не удалось превзойти уровень 30 000 гамм при таком же поле поляризации.
В связи с этим постоянная малогабаритных магнитных систем преобразователей определяется в основном максимальным входным сигналом /у. макс. Например, при /у. макс —100 мка постоянная магнитной системы не должна превышать 3* 105 гамм/ма; при /у. макс^ = 100 ма+3 • 102 гамм/ма и т. д.
Таким образом, чувствительность находится в сочетании с учетом возможного потребляемого тока, т. е. допустимого входного сопротивления преобразователя.
Стремление к чрезмерному увеличению чувствительности за счет постоянной магнитной системы может привести также к увеличению динамических погрешностей из-за переходных процессов установления поля в' зоне спиновой системы (см. связь поз. 40 с поз. 28 на рис. 4-17). Это явление для магнитных систем типа колец Гельмгольца несущественно, так как их постоянная времени обычно не
превышает 10-5—10-4 сек. Наиболее важным фактором является здесь увеличение температурных погрешностей и повышение требований к точности работы систем термостатирования, так как температурный дрейф постоянной магнитной системы приводит к изменениям крутизны преобразования:
|
|
Степень ослабления помех в различных частотных диапазонах, в частности, при нулевой частоте помехи о)п=0, в диапазоне входных сигналов (Оп^сэном и при высокочастотных помехах определяется типом мазера и функциональной схемой. Помехоустойчивость дифференциальной схемы преобразователя исследована в § 2-3, где показано, что для этой схемы имеются зоны нечувствительности к наиболее опасным помехам типа градиентов поля и вариаций градиента.
К числу случайных погрешностей отнесены случайные составляющие сдвигов частоты мазера из-за флуктуаций температуры окружающей среды, а также влияния температуры на стабильность фазы в цепи обратной связи и изменения постоянных составляющих внешних полей, приводящие к появлению мультипликативной, т. е. 'возрастающей с ростом сигнала, систематической погрешности, например, типа ориентационного сдвига частоты мазера. Практически все случайные температурные погрешности, связанные с изменением параметров магнитной системы, сильно коррелированы. Существенной корреляцией отличаются также случайные погрешности, связанные с контактными э. д. с., которые могут возникнуть из-за наличия разнородных материалов в конструкции датчиков.
Учитывая, что по вопросам стабильности параметров магнитных мазеров уже имеются систематизированные исследования причин сдвигов их частоты в стационарных режимах, основное внимание необходимо уделять анализу специфических для техники преобразования погрешностей, связанных с изменением поля поляризации (поз. 9) у погрешностей систем обработки частоты (поз. 5) и динамических ошибок (поз. 28).
В § 1-4 и 4-2 были приведены порядки величин сдвигов частот мазеров, существенно важных для техники преобразования сигналов постоянного и переменного тока в частоту следования импульсов.
Основная задача, решаемая при проектировании устройств первичной обработки информации, к которым относятся, в частности магнитометрические преобразователи, заключается в разработке таких функциональных узлов этих устройств и требований к ним, которые наилучшим образом обеспечивают реализацию операций, предусмотренных техническими требованиями по предварительной об-
работке и преобразованию информации, и, кроме того, удовлетворяют критериям стоимости и надежности [Л. 11].
Последовательность разработки протонно-прецессионных преобразователей, этапы которой изображены на рис. 4-18, обеспечивает выполнение требований, предъявляемых к ним и к точности измерения контролируемых параметров. Это требует обеспечения опреде
Ленного отношения амплитуды э. д. с. сигнала к среднеквадратическому напряжению шума за время измерения, которое аналитически определяется из условия (4-4).
Приведенный в предыдущих главах анализ принципов построения и основных характеристик магнитометрических преобразователей дает возможность сопоставить их параметры с поставленными техническими требованиями (этап І), сравнить их по интересующим нас критериям с другими преобразователями (этап 2) и сделать вывод о целесообразности разработки для некоторой конкретной системы контроля устройств первичной обработай информации, основанных, например, на использовании явления свободной ядерной прецессии.
Проектирование преобразующих устройств необходимо проводить, исходя из требований к структуре системы контроля в целом [Л. 34]. Такой подход облегчает оптимизацию связей между параметрами проектируемых блоков и параметрами других функциональных устройств системы. Это позволяет определить ограничения 3 на характеристики и параметры проектируемого устройства, выполнение которых необходимо для согласования контура обработки информации с системой, контролируемым объектом и для обеспечения его работоспособности в реальных условиях.
Перечень ограничений 3 позволяет иметь исходные данные как для принятия решения по конструктивному оформлению узлов и выбору элементов из числа типовых (18), так и для аналитических расчетов, что отражено на схеме рис. 4-18 связями этапа 3 с этапами 5, 7 и 8.
Как следует из приведенной схемы, выполнение условия 9 может быть достигнуто за счет поиска оптимального сочетания параметров чувствительного элемента 4 и магнитной системы 6 при условии соответствия их критериям стоимости и надежности (этап 14). іПри этом (необходимо учитывать ограничения на ©ес q, габариты V, ток поляризации /Р, максимальный ток управления /у, максимум частоты /о, объем рабочего вещества датчика Q, оказывающий существенное влияние на амплитуду сигнала прецессии, а также время преобразования Тазгл, зависящее от требуемой точности и отношения сигнал/шум.
Расчет собственных параметров датчика из условия максимума сигнала прецессии на этапах 4, 5 может быть проведен по методике, изложенной в работе |[Л. 51], которая предусматривает связь характеристик датчика, его геометрии и конструкции с э. д. с. сигнала.
Выбор типа и расчет параметров магнитной системы (этап 6) обеспечивают получение максимальной однородности магнитного поля в объеме датчика при минимальных габаритах системы.
От выбора типа магнитной системы в определенной степени зависят характеристики эталонных и испытательных сигналов (этап 15), используемых в данной системе контроля. На точность расчета неоднородности поля в объеме датчика на этапах 7 и 8 влияет принятое допущение о равномерности распределения витков обмотки (этап 16) по сечению прецизионной магнитной системы. Ниже оно проанализировано на конкретном примере. Допущение о равномерности распределения может способствовать введению обратных связей от этапа 9 — проверки 'выполнения ограничения на отношение сигнал/шум — к этапам 4 и 6
Для исключения ошибок в определении» величины неоднородности поля вместо допущения 16 в процессе проектирования может быть введен алгоритм расчета напряженности поля, учитывающий статистическим путем распределение витков по сечению обмотки магнитной системы.
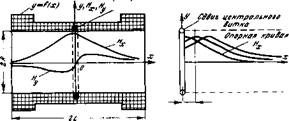
Тогда, используя приведенный выше алгоритм расчета полей Нх и Ну кругового контура, суммарную напряженность в рассматриваемой точке рабочего объема датчика можно определить в результате последовательного сдвига опорной кривой Hx = f(x, у)
(рис. 4-19,а), рассчитываемой для центрального витка с предельной точностью. Практика таких расчетов на ЭЦВМ показывает, что при использовании семи полиномов Лежандра погрешность при отбрасывании остаточных членов в формуле (4-10) оказывается меньше
ю-
Алгоритм для вычисления суммарной составляющей поля Нх1 для каждого конкретного значения х записывается для многослойного соленоида в виде
|
|
где L — линейный размер магнитного контура по оси х, выраженный в числе шагов обмотки; k — выраженный таким же образом порядковый номер витка обмотки, считая от центра контура; i, j — параметры, учитывающие симметрию задачи при сдвиге расчетного витка (рис. 4-19,6); по — число слоев обмотки, которое принято четным для уменьшения погрешности из-за влияния пространственной формы витка, т. е. изменения радиальной составляющей поля витка из-за разворота его плоскости от плоскости сечения на некоторый угол Yo> в общем случае непостоянный по длине витка.
Аналогичным образом может быть построен алгоритм расчета поля и для магнитных систем другого типа.
Типовые расчеты целесообразно выполнять с перфорированием значений промежуточных сумм, которые могут быть в последующих расчетах введены в машину без потери времени.
• Приведенный способ моделирования поля позволяет расширить границы использования указанного метода для расчета магнитных систем с произвольной формой огибающей обмотки y=f(x). При этом следует отдавать отчет, что приведенный аппарат в целях экономии машинного времени должен использоваться в первую очередь для уточнения вида функции распределения неоднородности в реальных конструкциях магнитных систем.
|
|
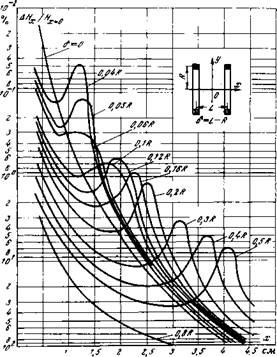
. Рис. 4-20. Изменение средней напряженности поля соленоида с постоянными ампер - витками ори изменении шага обмотай.
В качестве примера на рис. 4-20 показано изменение относительной величины средней напряженности магнитного поля в объеме однослойного соленоида с радиусом Я = 4 см, длиной 2L = 30 см при постоянстве ампер-витков Iw = const в зависимости от шага обмотки, первое значение которого было 'принято равным 1 мм, а затем последовательно уменьшалось до значения 2~7 мм.
Графики рассчитаны для составляющей Нх по опорной кривой в алгоритме (4-12), полученной из соотношения для одиночного витка >[см. формулу (4-10)] при числе полиномов Лежандра, автоматически ограничивающих ошибку расчета поля погрешностью порядка 10-8—10~9.
Расчеты были произведены для точек с координатами х и у, ограниченными размерами камеры поглощения (у^2 см, х^.5 см). Кривая с индексом у=2(1, II) относится к вариантам расчета на первом и втором шагах при у=2, кривые г/=0,5(/, VI) и г/=0,5(/, VII) к первому и последнему вариантам при у=0,5. Правая цифровая шкала относится к пунктирным кривым. Анализ данных вскрыл интересный факт локальной зависимости напряженности поля от технологии изготовления обмотки, причем уровень поля может отличаться для соленоида, с большим диаметром витков от поля соленоида на миниатюрном проводе диаметром порядка нескольких сотых миллиметра на 0,01—0,03% при неизменных полных ампер-витках.
В связи с этим после изготовления магнитных систем целесообразно проводить тщательное сравнение их постоянной с постоянной прецизионных магнитных систем одним из разработанных е метрологии методов.
Рассмотренный аппарат применим для статистического моделирования магнитных систем преобразователей, когда координаты витков обмотки изменяются случайно, например, сдвигаются от идеального положения на величину, не превышающую шага витка.
Особое внимание с ТОЧКИ зрения соблюдения условия Лит. т^ ^Аифакт, т. е. соотношения между фактическим и требуемым отношением сигнал—шум, проверяемою после завершения конструктивных расчетов и изготовления опытного образца преобразователя (см. рис. 4-18, этап 7/), следует уделить определению фактической неоднородности магнитного поля в объеме датчика, которая будет существенно зависеть от технологии изготовления датчика и магнит - ной системы.
Изготовление опытного образца позволяет уточнить основные характеристики и постоянные преобразователя, например, такие, как фактическое значение отношение сигнал/шум Аи. факт (этап 12), постоянную магнитной системы (этап 17), и выдать необходимые исходные данные для проектирования других блоков системы контроля и в первую очередь согласующих устройств и нормализаторов.
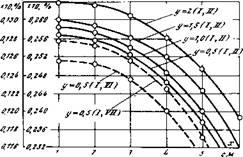
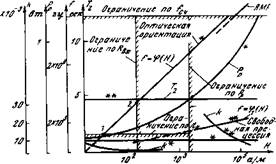
Сравнение различных типов преобразователей с точки зрения целесообразности их использования в конкретных условиях удобно проводить, анализируя ряд зависимостей, изображенных графически на рис. 4-21. Известно, что практическая реализация прибора лучше при более высокой чувствительности к изменению частоты в функции от поля, при меньшей мощности Рр, расходуемой от источника сигнала, меньшем коэффициенте усиления k (более простом усилителе), при более высокой линейности частоты от поля /=<р(Я) и меньших динамических погрешностях. Анализ должен проводиться при одинаковых постоянных магнитных систем и одинаковом управляющем токе /у. Уровень тока управления определяется, исходя из приведенных в § 1-1 требований к входному сопротивлению преобразователя (это ограничение обозначено на рис. 4-21 вертикалью
Rbx) •
Низкие частоты при малых постоянных магнитных систем могут оказаться неприемлемыми из-за большого времени контроля частоты /к {Л. 11], а чрезвычайно высокие частоты — из-за сложности соответствующих средств контроля (счетчиков). Это обозначено линией ограничения по /сч. Таким образом, рабочим участком функции /== = ср (Я) может оказаться ее участок 1—2. Из нескольких возможных случаев, удовлетворяющих рассмотренным условиям, выбираются те, которые обеспечивают (в зависимости от технических требований) либо меньшую потребляемую МОЩНОСТЬ Рр, либо более простой усилитель. Например, из анализа кривых /=ф(Я) и /= = Фі(Я), представляющих два сравниваемые метода, вытекает полное преимущество первого метода и неприемлемость для данных условий второго. Первый метод (оптическая ориентация) характеризуется также меньшими динамическими погрешностями, так как Т2*<&Т2**.
В связи с этим в технике преобразования так же, как при измерении слабых магнитных полей в магнитометрии, оказывается целесообразным использовать свободную ядерную прецессию (в криогенном варианте), динамическую поляризацию и оптическую ориентацию атомов или ядер.
|
Рис. 4-21. К выбору типа датчика для преобразователя * —овободная прецессия, ** —двойной оптический резонанс). |
Основные характеристики наиболее распространенных типов пре цизионных датчиков напряженности магнитного поля приведены выше в § 1-4.
Анализ этих данных, а также степени конструктивной разработки отдельных вариантов показывают, что в преобразователях угловых перемещений и электрических сигналов наиболее целесообразно использование гелиевых датчиков с наивысшей стабильностью нуля (лучше 0,1 гамм) и чувствительностью и освоенных к производству цезиевых (или рубидиевых) самогенерирующих устройств с высокими метрологическими свойствами.
[3] Обеспечивает максимальную стабильность частоты.
8 Обеспечивает высокое быстродействие при контроле частоты.
[5] Удобен для работы в зоне сильных градиентов магнитного поля.
[9] Параметры элементов, отмеченные звездочкой, подбираются при настройке.
должны обеспечивать достаточный для поддержания устойчивых колебаний постоянный фазовый сдвиг, малые фазовые искажения во всем диапазоне изменения напряженности магнитного поля и требуемый уровень усиления.
При использовании в датчиках камер поглощения размером 50X70 мм и интенсивности источника излучения порядка 5 -1015 фотонов в секунду (при освещенности фотодиода около 150—
[10] Материалы по этому усилителю и генератору (рис. 4-12) представлены А. Н. Козловым.
[11] Схема разработана инж. В. А. Наймушиным.

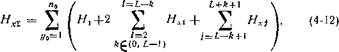
 Опубликовано в
Опубликовано в