Логические элементы
 25 декабря, 2012
25 декабря, 2012  admin
admin При использовании двоичной системы счисления с помощью логических элементов достаточно просто реализуются 20 функции алгебры логики, на основе которой строится большинство вычислительных машин и устройств автоматики. Физическая природа логических элементов может быть различной. Используют элементы релейные, диодные, пневматические, на интегральных схемах и др.
Зависимость между переменными величинами называется функциональной и обозначается Y = F (х) для одной переменной и Y = F (Xi, х2) для двух переменных. Величина х называется аргументом (независимой переменной); у — зависимая переменная, т. е. функция, ее значение определяется значением аргумента.
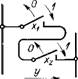
Функция повторения реализуется логическим элементом — повторителем. Входная величина х — состояние контактов реле: 1 — контакты замкнуты; 0 — контакты разомкнуты. Выходная величина у — проводимость электрической цепи: 1 — цепь замкнута; 0 — цепь разомкнута. При замкнутых контактах, т. е. при наличии сигнала на входе (х= 1), проводимость цепи существует (у= 1), при разомкнутых контактах (х = 0) проводимость равна нулю (у = 0). Выходная величина повторяет значение входной (табл. 1.3, п. 1).
Функция отрицания реализуется логическим элементом инвертором (табл. 1.3, п. 2), или элементом НЕ. Нормально замкнутые (нет сигнала) контакты х (х = 0) обеспечивают проводимость цепи (t/=l); сигнал х (х=1), приводящий к размыканию контактов, не обеспечивает проводимости цепи (у = 0).
При двух переменных (х и х2) на входе в логический элемент возможны четыре различные комбинации: 00, 01, 10, 11, каждой из которых может соответствовать значение у (выход), равное или 1, или 0. Релейным эквивалентом функции Y = F (хь хг) (проводимости цепи) будет состояние контактов х и хг (независимые переменные).
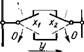
Функция логического сложения (функция ИЛИ, функция дизъюнкции) реализуется логическим элементом дизъюнктором. Сигнал на выходе элемента в зависимости от комбинации сигналов Xi и х2 на входе описывается следующим образом (хН-хъ = у): 0 + 0 = 0; 0+1 = 1; 1+0=1; 1 + 1 = 1,
|
Эквивалентность I/_____ и |
|
Х,...0 0 1 1 Х2...0 1 0 1 У..Л 0 0 1 |
|
Сложение по модулю т2 4О |
|
Х,...0 0 1 1 |
|
Х2...0 У- ..о |
|
1 0 |
Т. е. нулевое значение функция у принимает лишь в том случае, если х— 0 и Х2 = 0. Релейным эквивалентом функции сложения будут два нормально разомкнутых контакта х и х2, соединенных параллельно (табл. 1.3, п. 3) и обеспечивающих проводимость цепи (t/=l при проводимости цепи).
Функция логического умножения (функция И, функция конъюнкции) реализуется логическим элементом конъюнктором. Функция описывается следующим образом (xi - х2=у) : 0-0 = 0; 0-1=0; 1-0 = 0; 1-1 = 1, т. е. значение выходной величины у равно 1 только в случае, если на входе имеются два сиг
нала одновременно (х, = 1 и х2=1). Релейным эквивалентом функции являются два нормально разомкнутых контакта, соединенных последовательно (табл. 1.3, п. 4).
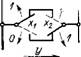
Функция равнозначности описывается таким образом:
Xi=x2 = {/:0 = 0=l; 0=1=0; 1=0 = 0;
1 = 1 = 1.
Значение функции равно 1, если х( = = х2. Релейным эквивалентом логического элемента (называется эквивалентностью) являются два переключающихся контакта, включенных последовательно (табл. 1.3, п. 5).
Функция неравнозначности противоположна функции равнозначности и часто называется функцией сложения по модулю т2 (табл. 1.3, п. 6):
Х ®х-2=у 0©0 = 0; 0® 1 = 1; 101=0.

 Опубликовано в
Опубликовано в