7.2.1. Постановка задачи и исходные уравнения

Для расчета кривых тока и напряжения необходимо совместное ре­шение уравнения энергии дуги и уравнений, описывающих электри­ческую цепь. Однако если уравнение энергии дуги сводится к линей­ному уравнению в частных производных, то решение задачи можно упростить. Для этого сначала решают уравнение энергии и находят динамическую вольт-амперную характеристику дуги - связь между мгновенными значениями силы тока и напряжения f(u, і) = 0. Далее находят совместное решение динамической характеристики и уравнений цепи, откуда и определяют все необходимые параметры.

В данном разделе принимают следующую постановку задачи. Рас­сматривают осесимметричную дугу переменного тока, горящую в ци­линдрическом канале без протока газа. Приэлектродные области не учитываются, считают, что вдоль оси все параметры постоянны. Пре­небрегают влиянием собственного магнитного поля и скин-эффекта на характеристики дуги.

Вследствие периодичности процессов нагревания и остывания газа в дуге существует периодическое радиальное движение газа от оси к стенке и обратно со скоростью о, зависящей от времени и переменной по радиусу канала. Радиальное движение электропроводного газа вы­зывает появление индуцированной составляющей напряженности элек­трических) поля Е^ - V-qVH, где Н - напряженность собственного

магнитного поля дуги. Однако оценки показывают, что в большинстве практически важных случаев значением можно пренебречь по срав­нению со значением напряженности электрического поля £, обуслов­ленной приложенным внешним напряжением.

Запишем теперь систему газодинамических уравнений без учета членов, содержащих Н:

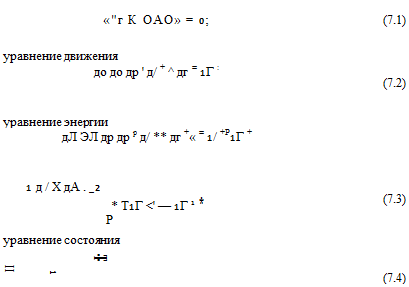В уравнении (7.3) q - член, учитывающий излучение дуги.

Произведем некоторые оденки членов этой системы. За характерную

скорость примем о = оя^/я, так как за время одного полупериода

элементарный объем газа не может пройти расстояние, большее ра­диуса канала г. Предполагая, что все члены уравнения (7.1) одного

порядка, из уравнения (7.2) получим

до

дг

Ар_____ я Ар __ .

2 "-22 ро ро» rQ

где р - средняя по сечению плотность газа; Ар - перепад давлений. Отсюда следует, что

. - -2 -22,2 Др и р о = ро» Гд/я.

Используем этот результат для оценки членов в уравнении (7.3):

где Ло - энтальпия на оси. При реальных значениях о выполняется

—2

условие у /Ло « 1, т. е. тепловая энергия газа в дуге намного боль­ше его кинетической энергии.

Здесь Ар и Ah - изменения соответствующих величин за полупериод.

Поскольку можно считать р = const (непроницаемые стенки канала и отсутствие осевого движения), то из уравнения (7.4) получим

К

Учитывая, что для горячего газа значение к близко к 1, получим 1 - 1/к « І, поэтому в первом приближении член (Ър/Ы) в уравнении

(7.3) не учитываем.

Несмотря на произведенные оценки членов, система уравнений все еще остается весьма сложной и нуждается в дальнейших упрощениях.

Будем считать, что радиус дуги (проводящего канала) не меняется во времени (гд = const) и определяется условием h(r) - Л( =

= const.

Примем Л/Ср = const = k^.

Электропроводность газа а является сложной функцией температуры (энтальпии). Заменим реальную функцию a(h) линейной зависимостью а = k (Л - Л).

о I

Л

Введем функцию N = / pdh и аппроксимируем ее линейной зависи - 0

мостыо N(h) = k^(h - Л^). Здесь к^ имеет смысл некоторой средней плотности газа.

Точный учет излучения дуги представляет собой весьма сложную задачу даже для стационарной дуги, не говоря уже о дуге перемен­ного тока. Поэтому в первом приближении будем считать радиационные потери q единицы объема пропорциональными энтальпии, т. е. q(h) =

=v*-v-

Таким образом, все свойства газа считаются линейными функциями его энтальпии (отсюда название ” линейная теория”).

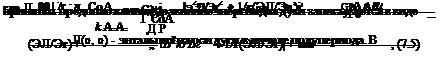Введем безразмерные величины

где и = Е1 - напряжение на дуге; / - длина дуги.

Краевыми условиями для этого уравнения являются постоянство

энтальпии на границе дуги Л(г, /) = 0, нулевая производная на оси

_ _ д __ ________

(ЭЛ/Эг)- = 0 и условие периодичности Л(г, г) = Л(г, г ♦ тг).

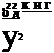Уравнение (7.5) решается методом разделения переменных. Положим Л = Л(г)Ф(г) и после разделения переменных получим

где »» - параметр разделения. 194

где /о - функция Бесселя нулевого порядка; - коэффициенты раз­ложения в ряд по функциям Бесселя; д - корни уравнения J^(x) = 0. Используя условие периодичности, получим

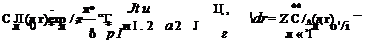2 2,

Поскольку ) являются собственными функциями рассматриваемой

задачи, то они линейно независимы, откуда следует, что

/1 /• М М ч

/ - V - » - -=7- * - о-

_ I,2 а 2 J

Но это равенство может выполняться только при одном значении мп>

так как в двух первых членах нет величин, зависящих от л.

Поскольку энтальпия не может быть отрицательной, то необходимо

положить л = 1 (так как на отрезке 0 < х < JQ(x) * 0).

Получим.

Ф(г) = ехр

0 р д

Из (7.6) можно получить выражение для определения эффективного напряжения на дуге V. Согласно определению

U2 = — / и dr.
я о

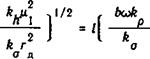Подставляя это выражение в (7.6) при т = тт и учитывая условие периодичности Ф(7г) = Ф(0) = 1, получим

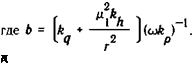Теперь общее решение принимает вид

Л(г. т) = / (и - l)drj.

где и = u/U.

В литературе величину 1/иЛ называют "постоянной времени” дуги, которая характеризует ее термическую инерционность. Однако мы не будем употреблять этот термин по двум причинам. Во-первых, тер­мином "постоянная времени” обычно пользуются применительно к экс­поненциальным процессам. В рассматриваемом случае процесс изме­нения энтальпии дуги во времени описывается сложной функцией вида exp f(r). Во-вторых, постоянной времени удобно характеризовать время реакции объекта на мгновенное изменение внешнего воздей­ствия, тогда как дуга переменного тока представляет собой сугубо нестационарный процесс.

Назовем b параметром нелинейности дуги. Смысл этого названия состоит в следующем. Дуга является нелинейным элементом электри­ческой цепи, т. е. ее сопротивление зависит от силы тока. Рассмот­рим влияние цепи на параметры дуги. Это влияние тем сильнее, чем больше проявляются нелинейные свойства дуги как элемента элек­трической цепи.

Параметр нелинейности характеризует отношение средней за Полу - период потери тепла из дуги за счет теплопроводности и излучения к среднему за полупериод количеству тепла, идущему на нагрев газа в дуре. Сумма этих двух величин равна, естественно, электрической энергии, выделяемой в дуге за полупериод.

Запишем теперь выражение для тока дуги:

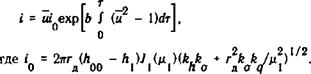(7.10)

Здесь Jі - функция Бесселя первого порядка.

Уравнение (7.10) представляет собой динамическую вольт-амперную характеристику дуги в установившемся (периодическом) режиме. Для нахождения форм кривых напряжения и тока это уравнение необходимо решить совместно с уравнениями электрической цепи вида f.(et и, /,

R, L, С) = 0 (у - количество независимых уравнений). Отсюда ясно, что общего решения для и и і не существует. Формы и И і будут за­висеть от конкретной схемы цепи.

На основании (7.10) легко показать, не привлекая соображений устойчивости, что в цепи, содержащей только источник питания и разрядный промежуток, установившийся режим горения дуги невоз­можен. Действительно, в такой цепи напряжение на дуге равно ЭДС источника, т. е. и = е sin г. При этом функция

а следовательно, и і удовлетворяют условию периодичности {/(0) = у(тт) только при 6 = 0. Однако из (7.8) видно, что случай 6 = 0 физически нереален. Отсюда следует, что если на разрядный про­межуток подать напряжение непосредственно от источника питания и каким-либо образом зажечь дугу, то эта дуга будет неустойчивой. Она либо погаснет, либо ток в цепи будет увеличиваться до тех пор, пока на режим цепи не начнет влиять внутреннее сопротивление источника или сопротивление токопроводов.