При некоторых условиях система авторегулирования вместо обес­печения стабилизации технологических параметров и компенсации иозмущений может начать их усиливать, тогда переходный процесс становится расходящимся, неустойчивым. Первые работы по иссле­дованию устойчивости систем автоматического регулирования при­надлежат русскому ученому А. М. Ляпунову.

Критерием устойчивости являются условия, при которых данная система может быть устойчивой. Проведем следующий опыт. К системе регулирования, разомкнутой ключом К (рис. 53, а), подключим гене­ратор синусоидальных колебаний (см. § 13).

На выходе разомкнутой системы хр через некоторое время уста­новятся периодические синусоидальные колебания. Частота этих ко­лебаний будет равна частоте приложенного к системе синусоидаль­ного возмущения.

При изменении частоты возмущающих колебаний будут меняться сдвиг между входными и выходными колебаниями А Т и отношение амплитуд (см. § 14). Будем увели­чивать частоту генерируемых ко­лебаний

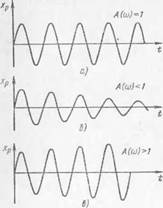
Рис. 54. Переходные процессы вбли­зи границы устойчивости:

а — граница устойчивости (Л(сй) —1). б — затухающий устойчивый переходный про­цесс (/4(<о)<1), в—расходящийся неустой­чивый переходный процесс (А(ш)>1)

Сдвиг по фазе тоже бу­дет увеличиваться. Подберем час­тоту г енератора так, чтобы выход­ные колебания отставали от вход­ных точно на един период, что со­ответствует сдвигу tp = 180е. Нет­рудно заметить, что при сдвиге 180° графики входных х и выходных хр колебаний в точности совпадают (рис. 53, б), если предположить, что амплитуды их колебаний оди­наковые.

Теперь отключим генератор ключом К и одновременно замк­нем систему. Вместо колебаний, получаемых от генератора, под­ключим в точности совпадающие с ними колебания с выхода системы. Поскольку на входе в систему сиг­нал не изменился, то и выходной остается неизменным, т. е. система будет продолжать то же движение (рис. 53,6), что и при е ключей но м генераторе. Эти незатухающие ко­лебания возникли из условия ф(со) = 180°; Л (to) = 1 (рис. 54, а), т. е. выходные колебания отстают от входных на угол 180°, а амплитуды равны между собой, их отношение равно 1.

Если при ф (со) = 180° амплитуда выходных колебаний будет мень­ше входных (рис. 54, б), то после замыкания системы амплитуда вы­ходных колебаний станет еще меньше, а это в свою очередь приведет к еще большему их уменьшению. В случае Л («) <; 1 переходный про­цесс окажется затухающим, т. е. все возникающие в такой системе возмущения затухают. Если амплитуда выходных колебаний больше амплитуды входных колебаний Л(<о);> 1 (рис. 54, б), то после замыка­ния системы амплитуда на выходе возрастет, что приведет к еще боль­шему ее же увеличению во время следующего периода колебаний, и т. д. Переходный процесс в этом случае будет расходящимся. Таким образом, при сдвиге tp(o) = 180° и А(со)> 1 система неустойчива; Л (со) < 1 — устойчива; Л (со) = 1 — находится на границе ус­тойчивости.

Амплитуда выходных колебаний может меняться в широких пре делах путем изменения параметров настройки регулятора, т. е. из­менения кр и Тиз. С изменением нагрузки технологического аппарата коэффициент усиления объекта будет существенно меняться (см. § 23) и устойчивая система при некоторых нагрузках может выйти за пре­делы устойчивости. Поэтому настройки регулятора выбирают с таким расчетом, чтобы был гарантирован запас устойчивости системы на іісех технологических режимах.

Рассмотрим эти условия на графиках амплитудно-фазовых частот­ных характеристик (см. § 14) Для построения точки частотной ха­рактеристики разомкнутой системы, соответствующей границе устой­чивости замкнутой системы, построим вектор из начала координат под утлом 180° (рис. 55, а), абсолютная величина (длина) которого равна

Конец вектора лежит на отрицательной вещественной полуоси, его координаты: —1; г0.

На рис. 55, б приведены АФЧХ трех разомкнутых систем. АФЧХ1 не охватывает точку с координатами (—1; г0) и соответствует устой­чивой системе. АФЧХ2 проходит через критическую точку—система, имеющая такую частотную характеристику, после замыкания ока­жется на границе устойчивости. АФЧХЗ охватывает точку с коор­динатами — 1; ї0; такая система после замыкания будет неустойчивой. Рассмотренное правило называется критерием устойчивости Найк - hиста — Михайлова, который имеет следующую формулировку: если амплитудно-фазовая частотная характеристика разомкнутой систе­мы не охватывает точки с координатами — 1; t0, то после замыкания этой системы отрицательной обратной связью она будет устойчива.

Критерий Найквиста — Михайлова позволяет судить об устойчи - иости САР еще до*ее замыкания на объект (по экспериментальным частотным характеристикам) и используется для определения основ­ных параметров объектов без самовыравнивания (см. § 22) воб итСб» не прибегая к снятию временных характеристик.

Для определения Коб ИТ об приведем регулятор к П-закону регулирования.

. Если система рабо­тает устойчиво после за­мыкания, то, увеличивая постепенно коэффициент усиления регулятора, добьемся того, чтобы в сис­теме возникли незатухаю­щие периодические коле бания, т. е. выведем сис тему на границу устойчи­вости, после чего опреде­лим период колебаний Ткр

и вычислим сокр (см. § 13) т. е. критическую частоту, при которой система нахо­дится на границе устойчи вости где кр. кр — критический коэффициент усиления ре­гулятора, при которому система вышла на границу устойчивости; сокр — кри­тическая частота, при ко торой система каходится| на границе устойчивости