Кинетика образования продольных сварочных. деформации и напряжений
 27 февраля, 2016
27 февраля, 2016  admin
admin В настоящем параграфе проследим за изменением во времени погонного об';сма продольного удлинения (укорочения) сварного соединения к одновременно - за изменением характера рас - : іеделения продольны* напряжений и всех составляющих дефор - наций. Иначе говоря, продолжим изучение процесса деформиро - -• ния полоски шириной Ах (см. рис.4Л, а). Если в § 4.2 мы рассматривали элементарные призмы, выделенные из этой подосин, изолированно друг от друга, то теперь рассмотрим процесс нх деформирования в совокупности, т. е. всей полоски в целом, пнозь отнесем размер полоски dx к единице длины и, прини - п;;я во внимание (4.2), изучим в некоторые последовательные моменты времени распределение температурных и пластических
деформаций, а такне определим площади их эпюр.
Начнем с момента t, , характерного тем, что в этот момент ширина зоны разупрочнения достигает максимума. Следовательно, процесс остывания охватывал до этого момента только указанную зону, где Т>7* , и изучение предыстории не требовалось, разгрузка в упругопластической зоне еще не нагналась. В соответствии с (3.21) tj=y*/(2a),a у* определяется
непосредственно! Ь уравнения (3.23) (|5т-4 )
На рис.4.5,а выполнено построение эпюр упругих и пластических деформаций в указанный момент времени в первом, а на рис.4.6 во втором приближениях по методу, изложенному в §4.2. Построение выполнено в соответствии со схемой рис.4.5,б. Кривая термического цикла заменена кривой распределения температуры по полусьчению пластины. В первом приближении предполагается отсутствие полных деформаций ( =0)
и при построении используется условие £.ер=-£т. Па всех графиках имеет место однозначное соответствие точек, обозначенных одинаковыми цифрами. Так, на графике Т(у) точка 2 характеризует температуру на расстоянии от оси валика; на графике lt(T) - температурную (недопущенную) деформацию;
на диаграмме ${,ь99) - напряжение, а отрезок 1-2 и равный ему отрезок 2-21 - пластическую деформацию и, наконец, на
искомых графиках <эх(.у) и £х(у) - напряжение и упругую деформацию, а отрезок 2-21 - пластическую деформацию. Эпюры пластических деформаций помечены косой штриховкой, а эпюра упругих деформзций - вертикальной. Видно, что последняя не уравновешена (упругих деформаций удлинения вообще нет). Поэтому возникают полные деформации, которые в соответ
ствии с (2.28) и (4.3) могут быть определены по формуле
![]() (4.5)
(4.5)
Здесь - площадь эпюры продольных пластических деформа
ций в первом приближении; 5Т - площадь эпюры температурных деформаций (площадь фигуры 032140); ширина пластины.
Второе приближение (см. рис.4.6) выполняется аналогично, но дилатометрическая прямая смещается параллельно себе на
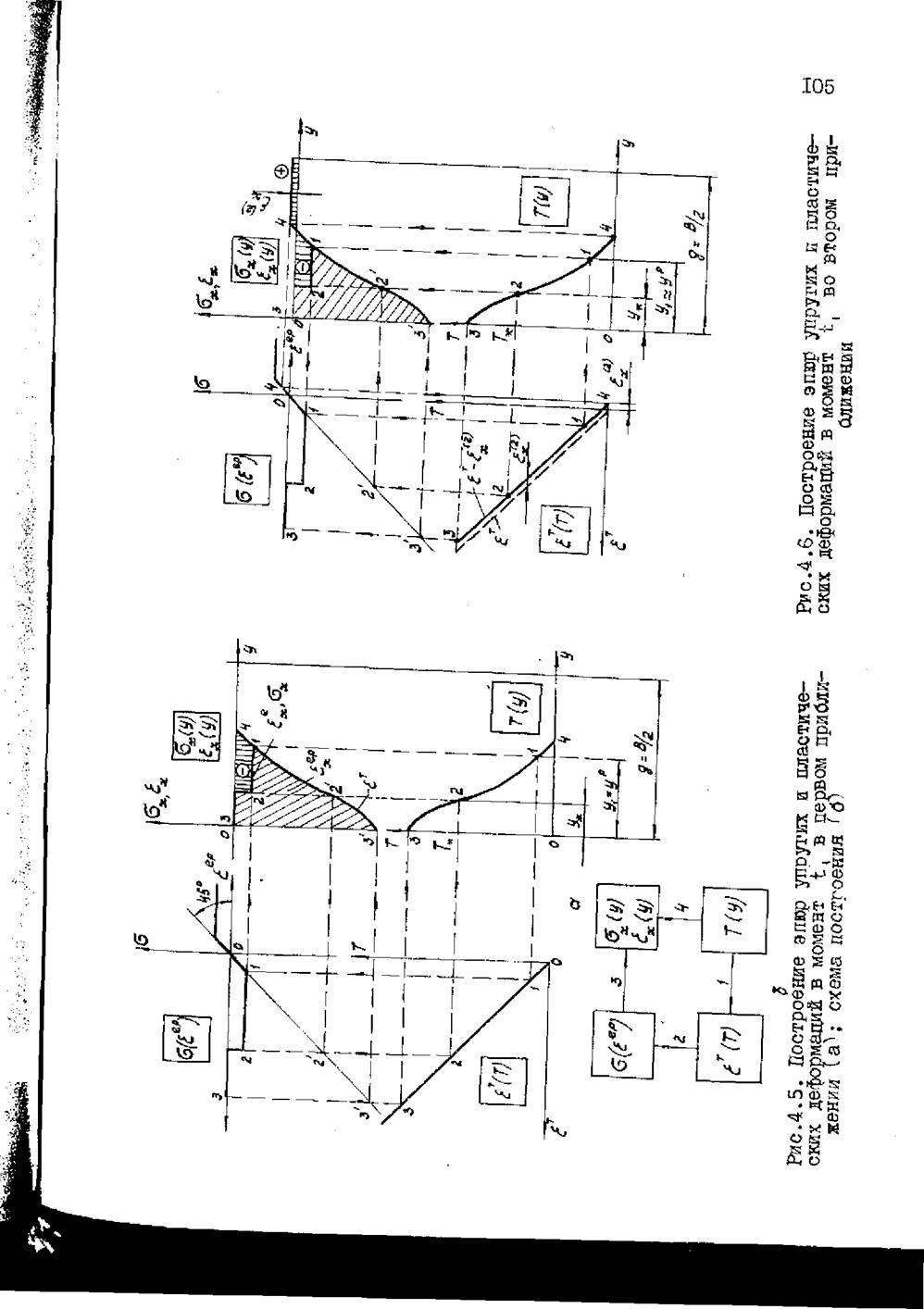
. Тогда ее новое положение характеризует - недопущенную
деформацию ет-е“- - єер и определяет соответствующие точки
на диаграмме б(£ер). В результате уточняется площадь эпюры пластических деформаций. Из построения ясно, что
![]() «5*»'
«5*»'
где £ур - ширина пластической зоны в рассматриваемый момент (в последующих приближениях принимается постоянной).
Подставляя (4.5) в выражение (4,6), получим уточненное значение площади пластических деформаций в виде
Таким образом, отпадает необходимость выполнять второе
приближение, так как по (4.7) уточняются результаты первого приближения. Более того, поскольку ДЛЯ 5т и 5^ можно получить аналитические выражения, вообще отпадает необходи
мость графических построений и решение можно представить в аналитическом виде, В самом деле, площадь эпюры температурных деформаций по определению
. (4.8)
в * в
Величину интеграла в этом выражении определим исходя из следующих соображений. В единичную полоску пластины при про
хождении через нее дуги ВВОДИТСЯ количество теплоты tyn={^/(Bf.)l
Объем этой полоски равен Bs. Следовательно, средняя температура полоски от введения в нее с^п равна
С течением времени средняя температура полоски понижается за счет теплоотдачи с поверхности. Учет теплоотдачи с
^ 4ь4т _
поверхности производится введением множителя е (см. главу 3). Поэтому средняя температура полоски с учетом теплоотдачи равна
VtЩ** • l4-9)
С другой стороны, средняя температура полоски выражается по формуле
Тер б т(1л|
В
Отсюда, учитывая (4.9), подучим
=Ttpb=(«Vn A cpsi)e bt. (4,10)
ъ
Подставляя (4.10) в уравнение (4.8), окончательно имеем
, (4-п>
где р(1)=е^ - функция теплоотдачи; изменяется от I (при t = 0) до 0 (при t—-=“ ); характеризует уменьшение площади эпюры температурных деформаций вследствие теплоотдачи в момент времени t.
Обозначим через 5о выражение
sT=iLin. (4.12)
гО tp S ■ * '
Величина характеризует площадь эпюры температурных деформаций без учета теплоотдачи. Тогда функцию p(t) можно рассматривать как отношение площадей эпюр температурных деформаций с учетом и без учета теплоотдачи
5Т
Итак, площадь эпюры температурных деформаций гложет быть определена в любой момент по аналитической зависимости (4.II). Она пропорциональна погонной энергии нагрева и обобщенной характеристике свойств металла oL/(cji) и изменяется во време
![]() ни по экспоненциальному закону. При обычных условиях
ни по экспоненциальному закону. При обычных условиях
мало (множитель e bt - і. ) и, следовательно:
с. р 5
Площадь эпюры продольных пластических деформаций $р составляет часть площади ♦ Обозначим отношение указанных площадей через J^x(t)=S^/S>o и назовем функцией продольных пластических деформаций. Очевидно, что с течением времени
площадь Ьх изменяется, в то время как неизменна. По-
этому функция jLx(t) характеризует изменение во времени площади эпюры продольных пластических деформаций. Так как
?>х<0 , а Ьт0>0 , то эта функция отрицательна, jtx(tH0 . В
рассматриваемый момент времени Скак и в последующие) площадь эпюры пластических деформаций также может быть определена аналитически (известны уравнения, ограничивающую эту площадь), но, поскольку наша основная задача - изучить физическую сущность процесса к выявить его особенности, мв сначаг - л а продолжим качественный анализ и лить затем приведем конечные результаты по вычислению функции. Из рис.4.6
видно, что $х составляет значительную часть площади 5Т .
Действительно, анализ показывает, что отношение этих площадей, т. е. значение jLx(t,) изменяется в весьма узких пределах: от -0,87 при с^п/Р < 40 Дж/см3 до -0,85 при /F
= 400 Дж/см3. Следовательно, в этот момент времени irxp>o, а
jix(t^ практически не зависит от жесткости (при 400
Дж/см3). Зная Ьт и 5Х, по формуле (4.5) определяем полные деформации в момент t{ , которые для краткости обозначим
(e-rMt,')') •
Перейдем теперь к следующему моменту ta, характерному тем, что ширина зоны, нагретой до температуры т* /г. ,
достигает максимума ( у^гу* , tg= ^). В этот момент часть сечения полосы (при y-cyd ) остывает, а другая ее часть (при
у>уг ) нагревается. Поэтому на рис.4.7 изобразим не только распределение температуры в рассматриваемый момент, но и кривую максимальной температуры для охлаждаемой области. Тогда, полагая в первом приближении ьх= 0, непосредственно получим аналогичным построением кривые распределения упругих и пластических деформаций. Например, для призмы, ! удаленной от оси шва на расстояние у5 , температура в момент ее максимального нагрева характеризуется точкой , ав рассматриваемый момент она понизилась и соответствует точке 3 (рис.4.7,г). Проводя горизонтальные линии от указанных точек до дилатометрической прямой, получим на ней соответствующие точки Зип и 3. Проводим от них вертикальные линии к диаграмме <э(бер') и, принимая во внимание, что с момента остывания начинается процесс разгрузки по линии Зт - 3, получаем
на диаграмме цикл изменения напряжений и упругопластических деформаций для этой призмы, характеризуемой ломаной линией 0 Пт'5 » Точка 3 определяет ее напряжения и упругоплаотиче - ские деформации в рассматриваемый момент. Видно, что на стадии остывания изменяются только упругие деформации (обратная пластика еще не началась). Поэтому пластические деформации призмы соответствуют отрезку между точками I - 3 m и равному ему отрезку 3 - З1 . Перенося его на искомый график, получаем нпачеяия пластических деформаций, а проектируя точку 3 - значения упругих деформаций. На рис.4.7 площади пластических и упругих деформаций показаны соответственно косой и прямой штриховкой.
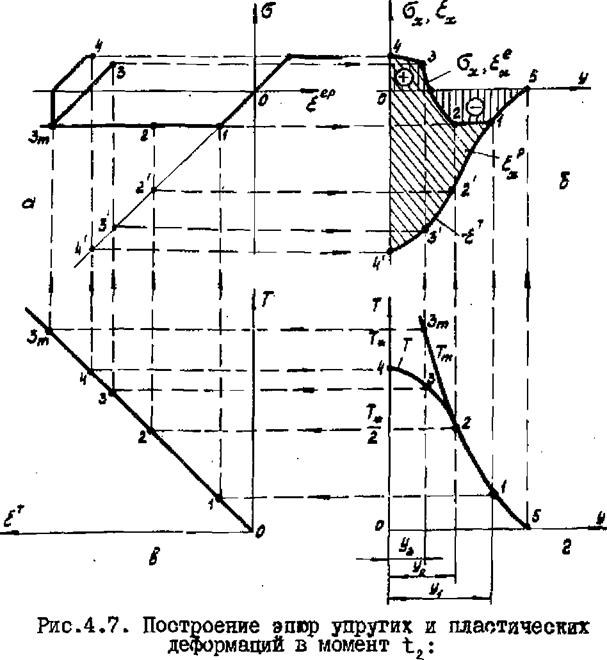 |
а - диаграмма ©Uef); б - эпюры деформаций и напряжений; в - дилатометрическая кривая; г - распределение Т и Тти в момент
Характерным для этого момента времени является возникновение в зоне шва растягивающих напряжений и расширение so-
не шва растягивающих напряжений и расширение эоны пластических деформаций. Площадь эпюры температурных деформаций (площадь фигуры 04'З12'150 превышает площадь эпюры пластических деформаций ( vxp > 0 ), и полные деформации, определяемые соотношением (4.5), положительны (е. х(Фг)>0 ); обозначим их для краткости га. Отношение эпюры к , т. е. зна
чение функции jix(ta) , изменяется также в весьма узких пределах (в зависимости от параметра tyn/F ) и мало отличается от Однако в последующие моменты функция jix(t) умень
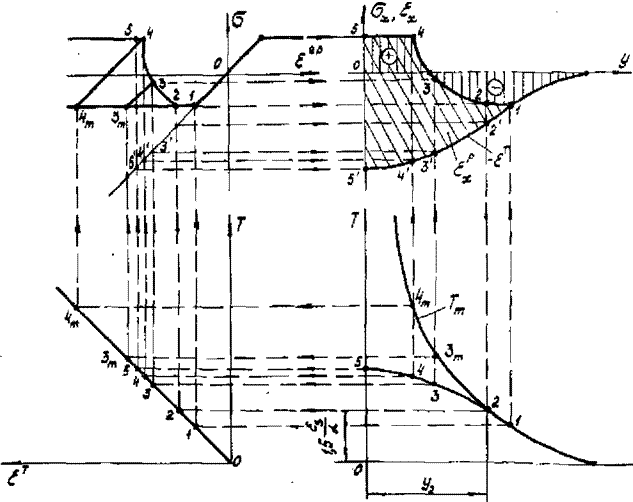
шается по абсолютной величине. Так, на рис.4.8 выполнено построение эпюр упругих и пластических деформаций для момента t3, характерного тем, что в этот момент наибольшую ширину имеет зона, нагретая до температуры І,5цЛі, . Упругая эпюра уже в первом приближении почти уравновешена, что означает
 |
|
приблизительное равенство <>T(t^ и |5х{Ц)|и, следовательно, малую величину е. х(1ц), которую далее будем обозначать ц. Отметим, что значение функции jLx(t3') зависит уже не только от
Ill
жесткости (параметра <П/Р ), но и от теплоотдачи. В зави
симости от этих факторов ja. x(t3') может быть как больше, так и меньше. Это означает, что в период, близкий к Ц,
объем удлинения переходит в объем укорочения и, соответственно, полные деформации меняют знак, переходя в отрицательные.
Наконец, рассмотрим состояние единичной полоски после полного остывания. Поскольку температурные деформации исчезают, а дилатометрическую кривую мы аппроксимировали прямой, то можно упростить построение и изобразить непосредственно под диаграммой <э(Еер') деформации, т. е. деформации,
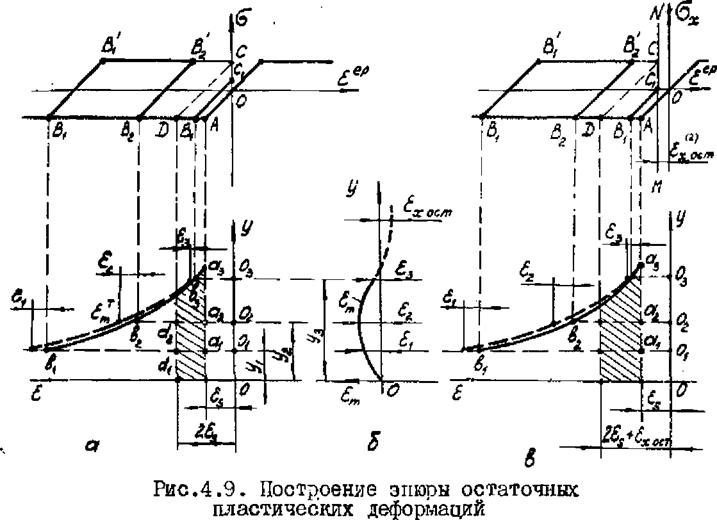
недопущенные в момент максимального нагрева соответствующих призм. На рис.4.9,а показана пунктирной линией кривая максимальных температурных деформаций e.1^=oLTm, а на рис.4.9,6- кривая полных деформаций, имевших место в момент максимального нагрева соответствующих призм £.т(у) . Последняя построена по результатам определения полных деформаций в моменты tx ta* Ц. Так, в момент времени t, максимальную температуру имела призма на расстоянии от оси шва.
Поэтому на расстоянии отложена полная деформация ц. Аналогично, полные деформации ьг и еъ характеризуют точки искомой кривой на расстоянии уг и у3 . Сплошной линией на рис.4.9,а показана кривая, характеризуючая деформацию которая и определяет начало разгрузки на диаграмме б'(гер) .
Так, например, недопущенная деформация в момент максимального нагрева призмы I соответствовала отрезку. Проектируем точку Ф* на диаграмму б(е, ер') в точку Б1 . От этой точки начинается разгрузка по линии при остывания и, далее,
пластическая деформация удлинения, характеризуемая отрезком В1,С, . Суммируя (с учетом знака) пластические деформации, возникавшие при нагреве (укорочения) и при остывании (удлинения) , получаем остаточную пластическую деформацию укорочения - отрезок АБ=сц&(. Охватывая все призмы по сечению, получаем эпюру остаточных пластических деформаций в первом приближении (заштрихованная площадь). Далее определяем по
уравнению (4.5)остаточную полную деформацию Так
pH)
как $х со, то и кривая £^(у1 может быть до
строена, как показано штриховой линией на рис.4.9,б. Следовательно, процесс деформирования при остывании заканчива-
ется у линии MN, отстоящей от оси 6 на расстоянии єхост,
лак показано на рис.4.9,в, на котором выполнено построение эпюры остаточных деформаций во втором приближении. В результате уточняется эпюра остаточных пластических деформаций.
*г
Отношение этой площади к 50 характеризует конечное значение функции. Его обозначим и назовем коэффициен
том продольного укорочения сварного соединения^
|
|
Таким образом, площадь эпюры пластических деформаций в любой момент времени может быть определена по выражению
- (4.13)
Значения функции продольных пластических деформаций в рассмотренные моменты (t,,ta, t3) могут быть определены из рис.4.10, а конечное значение этой функции, т. е. коэффициент продольного укорочения сварного соединения, - по формуле
JLX=-0,I|M In 0+6 ■ Ю'-* <*п /Fnp) , (4.14)
ИЗ
![]()
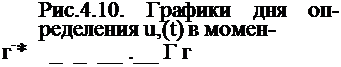
 Формула (4,14а) и графики рис.4.10 получены по изложенной методике при J. T* /е5 = б, £3:(ot,/(C. p)) = 400 Дж/см3 и условии Cfo/F4 400 Дж/см3.
Формула (4,14а) и графики рис.4.10 получены по изложенной методике при J. T* /е5 = б, £3:(ot,/(C. p)) = 400 Дж/см3 и условии Cfo/F4 400 Дж/см3.
Подставляя С4.И) и (4.13) в (4.3), получим уравнение процесса изменения погонного объема продольного удлинения (укорочения) единичной полоски пластины
(4.15)
![]()
![]() гДв *(t) = Ji(tV харак
гДв *(t) = Ji(tV харак
теризует площадь суммарной эпюры
температурных и пластических деформаций в момент времени t В соответствии с (2.28) зависимость полной деформации от воемени имеет вид
(4.16)
На рис.4.II показан характер изменения функций pft) и
![]()
![]()
![]()
![]()
![]() для частного случая наплавки валика на пластину из низ коуглеродистой стали в зависимости от времени. На том же ри - оунке показана сумма' этих функций (заштрихован
для частного случая наплавки валика на пластину из низ коуглеродистой стали в зависимости от времени. На том же ри - оунке показана сумма' этих функций (заштрихован
ная эпюра), которая характеризует изменение объема продольного удлинения (уко - о рочения) сварного соединения на единицу его длины, - qs Из рисунка видно, что функция ц>хф сначала воэрас - -<,о тает, затем уменьшается, переходя в отрицательные. визначення. Следует отметить,
что функция (ox{t) достига - Рис.4.II. Изменение функции
ет своего nnp w. irt. ww. ft at>a ТЄШЮОТДаЧИ, ПрОДОЛЬНЫХ И ПО-
т своего предельного зна - перечных пластических дефор-
чения раньше, чем заверши* маций в зависимости от времени
ется процесс остывания пластины, и что при t—~ yx(t)=^xi так как р(£У=0.
Таким образом, в процессе сварки и доследующего остывания объем продольного удлинения (укорочения) непрерывно из- Ф меняется. После завершения этих изменений он приобретает конечное значение - объем продольного укорочения сварного соединения, который пропорционален площади эпюры
остаточній пластических деформаций Sx Определе
ние объема продольного укорочения сварного соединения является одной из основных задач теории сварочных деформаций и напряжений. Приближенное определение его величины, при некоторых условиях сварки, выполнено в следующем параграфе без рассмотрения кинетики процесса. Но прежде чем перейти к этой задаче, необходимо обобщить полученные результаты, определить границы их применимости и сделать выводы по анализу кинетики образования продольных деформаций и напряжений при сварке.
Вше нами рассматривались деформации и напряжения при наплавке валика по оси пластины (сварке встык полос равных ширин). Однако полученное решение легко распространяется на случаи сварки полос разной ширины и балок произвольных сечений. Действительно, принимая во внимание, что зона пластических деформаций охватывает незначительную часть площади сечения свариваемых элементов и что центр тяжести объема удлинения (укорочения) сварного соединения совпадает с осью шва,, можно осреднить полные деформации в зоне пластики и принимать их равными полнда деформациям на оси шва &ж . Тогда, в соответствии с (2.45) и (4.15), можно записать, что
£хш^==1,хРАпр=Ух^ср’ 1
т. е. £.хш определяется по зависимости, аналогичной (4.16) для полной деформации по центральной оси £Xo(t) , но с заменой F на ГПР. Знание полных деформаций в двух точках, а именно на оси шва и в центре тяжести сечения, достаточно для
х) Некоторые авторы называют эту величину суммой оставшихся после сварки пластических деформаций укорочения и обозначают ЗЕГ.
хх) При несоблюдении этих условий решение требует уточнения.
расчета кривизны. Отметим теперь ограничения полученного решения.
X. Средняя температура нагрева сечения должна быть меньше (докритяческий режим). В частности, для низко
углеродистой стали ТСР ^ 100°С, что обеспечивается при
400 Дж/см3. В противном случае процесс выравнивания
температуры заканчивается раньше, чем ширина зоны пластики достигает наибольшей величины. Поэтому в данном случае требуется определение температуры с учетом отражения теплового потока от продольных кромок, а также более строгая оценка влияния полных деформаций (они одного порядка с максимальными температурним деформациями у границы пластической зоны) .
2. Центр тяжести объема удлинения (укорочения) должен совпадать с осью шва или незначительно смещаться от нее. Инаг - че принятое усреднение полных деформаций в пределах зоны пластических деформаций приводит к существенным погрешностям.
3. Ширина зоны пластических деформаций в каждом из соединяемых элементов должна быть меньше его полуширины. Иначе также необходим учет влияния на распределение температуры отраженных источников тепла (см. § 4,7). При сварке элементов судовых конструкций эти ограничения обычно не накладываются и приведенная методика может быть применена без уточнения. В противном случае требуется учет указанных дополнительных факторов.
Выполненный анализ кинетики сварочных деформаций и напряжений позволяет сделать следующие выводы.
1. Погонный объем продольного удлинения (укорочения), а
следовательно, и параметры деформации сечения в
процессе сварки и последующего остывания непрерывно изменяются по общему аакону и одновременно изменяю, знак. Все указанные величины пропорциональны погонной энергии нагрева и обобщенной характеристике теплофизических свойств металла
2. Конечное значение погонного объема укорочения сварного соединения зависит от величины полной деформации в мо-
х) При эакритических режимах коэффициент продольного укорочения jix уменьшается с увеличением tyn/F.
мент достижения пластической зоной наибольшей ширины. Полная деформация в указанный момент может принимать как положительные, так и отрицательные значения в зависимости от жесткости и теплоотдачи. Поэтому учет конечной жесткости может приводить и к уменьшению, и к увеличению ггх , однако при
tyn/F 4 400 Дж/см^ (докритический режим) поправки незначительны и ими можно пренебречь,
3. Е зоне шва (повторных пластических деформаций) остаточные пластические деформации укорочения превышают по абсолютному значению ц на величину ^ /

 Опубликовано в
Опубликовано в