Теплоотдача труб в спокойном, воздухе

Ф. Вамслер ** исследовал трубы с внешним диаметром 20,5; 33; 48; 59; 76; 89 мм, причем температура трубы достигала более 240° С. Окружающая среда имела комнатную температуру. Наи­более существенные результаты измерений даны в табл. 3.

Таблица - 3

Коэффициенты теплоотдачи конвекцией для труб, расположенных горизонтально, в спокойном комнатном воздухе (по Вамслеру) Разность температур, ®С Материал трубы Диаметр М 50 1.00 150 Ковкое железо. . '...................................... 0,033 7,0 7,8 8,7 Ковкое железо. '........................................ 0,059 6,6 7,4 8,3 Ковкое железо........................................... 0,089 4,7 5,5 6,3 Литейный чугун......................................... 0,059 5,8 6,6 7,4 Медь...................................................... ^ 0,059 8,1 6,8 8,1 * См. дополнительно Рубинштейн Я. М., Метод аналогии с диффузией и применение его для исследования теплопередачи в начальном участке трубы, Сб. ВТИ «Исследование процессов регулирования, теплопередачи и обратного охлаждения», ГОНТИ, 1938. (Прим. ред.) ** W а m s 1 е г F., Die Wдrmeabgabe geheizter Kцrper an Luft. Forsch. — Arb.-Geb. Ing. Wes., H. 98/99 (1911).

Ф. Ваомлар нашел (приближенную фсрмулу для (коэффициента тест - лосквдачи конвекцией гаршомтальных труб в опокой нам воздухе

А /0,233

А = 0,95----------- ккал/м2 • час • °С. (223>

С10,3

Коэффициент теплоотдачи в случае медной трубы оказался на 10% »выше, чем для трубы из ковкого железа. Остается неясным^ существует ли фактически такая большая разница или же это вызвано ошибкой, связанной с трудностями учета потерь тепла ■ излучением, кот#£>ые вызывают эту разницу? В свое время Ф. Вамслер применял еще коэффициент излучения черного тела,, равный 4,61 ккал/м2'-час-град*у который, по последним данным, является заниженным на 7%. Гипсовая обмазка труб изменила» их теплоотдачу, но очень незначительно, так что этим изменени­ем состояния поверхности практически можно пренебречь.

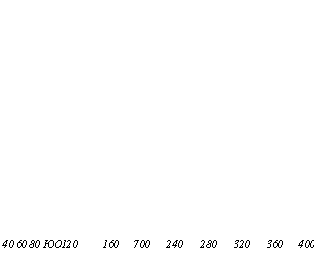
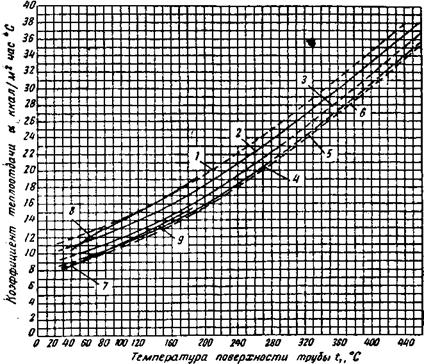
Р. Г. Гейльманом* в 1924 г. была исследована потеря тепла трубой, расположенной горизонтально, в спокойном воздухе. Бы­ли взяты диаметры трубы 25,4; 76,2; 254 мм при температурах от 50 до 465° С, что значительно расширило область измерений по диаметрам и температурам. Одновременно им было установлено относительно сложное эмпирическое уравнение, по которому и рассчитаны коэффициенты теплоотдачи для труб диаметром 13 и 457 мм. На рис. 13 приведены результаты, полученные Гейль­маном. Экстраполированные части кривых, являющиеся продол­жением кривых, построенных по результатам опытов, показаны пунктиром. Если от общих коэффициентов теплоотдачи, изобра­женных на рис. 13, вычесть (коэффициент теплоотдачи излу­чением), то получив коэффициенты теплоотдачи конвекцией’ (рис. 14). При этом излучение рассчитывают по уравнению**

(225)

4 = ккш1мКчас - (224)' Если коэффициент теплоотдачи излучением определить», руководствуясь уравнением (1), то с другой стороны, количество передаваемого тепла

Q = аиз —12) ккал/м2 • час.

Сравнивая уравнения (224) и (225), получим коэффициент теп­лоотдачи излучением * Heilman R. Н., Mellon Inst., Heat Transmission from Bare and in­sulated Pipes, Industr. Engng. Chem., 16 (1924), Hai, p. 451/58. **- Ср. с уравнением (393).

Где

Тх и Т2 — абсолютные температуры (°К=°С+273) излучаю­щей и облучаемой поверхностей; tl Иt2 — соответствующие температуры в °С;

С —.коэффициент лучеиспускания, который примерно. равен 4 (см. таблицы приложения).

Рис. 13. Коэффициенты теплоотдачи для трубы, расположенной горизон­тально. в спокойном воздухе (конвекция + излучение). По данным Гейльмана, <1 равно: / — 73 мм 2 — 25,4 мм (замерено); 3 — 76,2 мм: 4 — 254 мм (замерено); 5 — 254 мм 6 — 457 мм (экстраполировано); по данным Ко­ха, й равно: 7 — 100 мм; 8 — 74 мм 9 — 100 мм

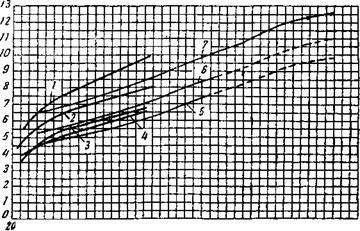
На рис. 15 изображены кривые, характеризующие изменение а5 в зависимости от температуры поверхности ^ для различных коэффициентов лучеиспускания С, причем температура окру­жающей среды принята постоянной: ^2=Ю°С. Суммарная поте­ря тепла излучением, теплопроводностью и 'конвекцией опре­деляется по уравнению

Я = (ак + аиз) (к — *2) ккал/м2 • час. (227)

Температура поверхности тру8ы ^, сС *

Коэффициент теплоотдачи UK, ккал/м2час °С

40 60 80 ЮО120 160 700 240 280 320 360 400

Рис. 14. Коэффициенты теплоотдачи для трубы, расположенной го­ризонтально, в спокойном воздухе (конвекцией):

По данным Коха, й равно: / — 74 мм; 2 — 31 мм; 5 — 68 мм; 4 — ЮО ММ по данным Гельмана, й равно: 5 — 254 мм; 6 — 76,2 мм 7 — 25,4 мм

О SO 100 200 300 400 500 600 700 800 Температура излучающей поверхности t1$ °С

Рис. 15. Коэффициенты теплоотдачи путем излучения

9 А. Шак

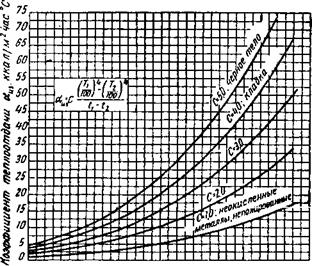
Дальнейшие опыты по измерению потерь тепла трубами принад­лежат В. Коху [60]. Они были проведены в Мюнхенском институте технической физики. В. Кох для исследования взял четыре сталь­ные трубы внешним диаметром 14, 31, 68 и 100 мм, внутри кото­рых был помещен электрический нагреватель. Длина труб состав­ляла 1,9 м. Наряду с горизонтальным Кох исследовал также вертикальное и наклонное положения труб. Результаты опытов, полученные при горизонтальном расположении трубы, изображе­ны на рис. 13 и 14 вместе со значениями, полученными Гейльма - ном. Результаты Коха и Гейльмана совпадают довольно точно, если пренебречь уменьшением коэффициента теплоотдачи по Ко­ху при малых температурах. При этих температурах измерения, проведенные Кохом, должны быть более точными, так как он с большей точностью устанавливал истиеую темшратуру воздуха и стен помещения, где проводились опыты. При оценке своих ре­зультатов Кох применил теорию подобия и вследствие этого по­лучил известные формулы теории подобия для теплоотдачи кон­векцией, которые содержат температуропроводность, вязкость, давление и другие параметры окружающего газа. Однако по этой же причине формулы неудобны для воздуха, так как не да­ют большей точности по сравнению с простейшей эмпирической формулой. Но для других газов (кроме воздуха) они, конечно необходимы. Рис. 13 позволяет непосредственно определить ис­комый коэффициент теплоотдачи. Опыты Гейлымлна следует счи­тать достаточно надежными, так как они были проведены на трубах с внутренним электрообогревом, который применялся в течение семи лет для исследования изоляционных материалов и многократно контролировался другими методами.

Со значениями, полученными Гейльманом, совпадают резуль­таты опытов, проведенных Е. Гриффитсом и К. Джейкмэн (Na­tional Physical Labor, Teddington) [61]. Эти исследователи прово­дили свои эксперименты на двух трубах длиной 3,5 м и диам. 4,5" и 9" (что составляет соответственно 114 и 228 мм) по четы­ре^ режимам: с внутренним обогревом паром; с внутренним обо­гревом при помощи электронагревателя; с установкой защитных колец на концах трубы; с установкой калориметров на концах для определения влияния концов трубы.

В этих опытах вообще не обнаружено влияние величины диа­метра; очевидно, что (при дтаметре более 100 мм, его влияние ма-

Ло. Найденные коэффициенты теплоотдачи (излучение + конвек­ция) могут быть вьиражены независимо от диаметра формулой

А = 8,2 + 0,00733 • /1,ззэ ккал/м2час-°С (228)

Или также

А = 8,2 + 0,00733t ккал/м2-час*°С. (228а)

Значения а совпадают с достаточной точностью. в соответствую­

Щей области кривой, данной Гейльманом; правда, действительны они лишь для труб с диам. выше 100 мм. Опыты Ф. Вамслера так­же довольно точно совпадают с результатами исследования Гейль - ( мана. Сообразно с этим кривые, данные на рис. 13, можно рас - ' сматривать как наиболее точно на сегодня отражающие значения теплопотерь трубами, расположенными горизонтально в спокой ном воздухе.

Влияние наклона труб было определено на той же установке посредством большого числа измерений. Получилось, что труба с наклоном оси 45° теряет путем конвекции и теплопроводности около 92% того количества тепла, которое теряет труба, лежа­щая горизонтально. Так как влияние излучения оставалось по­стоянным, можно считать, что общая потеря тепла трубы, на­клоненной под 45°, составляет примерно 96%тепла, теряемого горизонтально лежащей трубой.

Более сложными оказались соотношения в случае вертикаль­но расположенной трубы. При этом. получается коэффициент теплоотдачи, сильно изменяющийся по высоте трубы. К нижнему ее концу »коэффициент теплоотдачи довольно быстро падает с относительно высокого значения до минимума, который наблю­дался на расстоянии примерно 0,5 м от нижнего конца трубы; затем, смотря по условиям, он либо поднимается до постоянного значения, либо остается неизменным. Результаты опытов {приведе­ны в табл. 4. Они относятся к коэффициенту теплоотдачи одной конвекцией от вертикально расположенной трубы в спокойном воздухе при комнатной температуре.

Следовательно, наибольшая часть трубы длиной 2 м нахо­дилась в области постоянного коэффициента теплоотдачи.

К этим значениям следует еще прибавить коэффициенты теп* лоотдачи излучением, которые даны на рис. 15 для различных коэффициентов излучения. Для железных труб коэффициент из­лучения вообще лежит в интервале 4—4,4; то же «самое относит­ся »к изолированным трубам с бандажами или земляной обмаз­кой. Если при вертикальном и горизонтальном расположений труб сравнить значения коэффициентов теплоотдачи, данные на рис. 14 и в табл. 4, то получается, что коэффициент теплоотда­чи <*к в случае вертикальной трубы при температурах от 130 9*

Таблица 4

Коэффициенты теплоотдачи конвекцией при вертикальном расположении

Трубы по Коху

1. Диаметр й = 14 мм 71,5 87,0 110,3 132,0 142,5 7,21 8,11 8,43 8,69 8,77 2. Диаметр й = 31 мм

31,4 44,1 53,6 55,1 74,3 2,44 2,85 3,05 3,17 3,45 109,8 126,2 146,3 158,0 173,8 3,86 4,01 4,18 6,02 7,06 [иаметр сі = 100 мм 28,7 41,6 59,3 77,6 91,4 2,49 2,81 3,13 3,83 3,74 142,1 158,4 160,8 176,9 179,5 7,03 7,28 7,15 7,38 7,49

126,9 6,51

Температура трубы, °С. Коэффициент теплоотдачи

Температура трубы, °С. Коэффициент теплоотдачи

Температура трубы, °С. Коэффициент теплоотдачи Температура трубы, °С. Коэффициент теплоотдачи

Температура трубы, °С ' . Коэффициент теплоотдачи Температура трубы, °С. Коэффициент теплоотдачи

92,0	127,4	161,8	164,1
6,42	7,11	7,83	7,72

151,3 9,00

3. Диаметр й = 68 мм

87,2 3,63 158,0 7,29

До 150° С значительно меньше (примерно составляет 65%) по сравнению с величинами, полученными на горизонтальных тру­бах при температурах от 130 до 150° С, и при том у более тол­стых труб выше, чем у более тонких. В то время ка« при 160° теплоотдача конвекцией от вертикальной трубы диам. 31 мм больше примерно лишь на 1% по сравнению с горизонтальной трубой, теплоотдача от трубы диам. 100 мм при 160° С уже на 15% больше теплоотдачи конвекцией в случае (горизонтальной трубы.

Если для более точных расчетов принимать во внимание пре­дыдущие результаты, то все же необходимо отметить, что най­денные расхождения вследствие влияния излучения независимо от положения и размера трубы при определении общей отдачи тепла уменьшаются примерно вдвое. Кроме того, расхождения в нижней части вертикально стоящей трубы и в верхней ее части имеют противоположные знаки. Следовательно, с точностью, до­статочной для большинства случаев, найденную для горизонталь­ных труб теплоотдачу можно применить и к вертикальным тру­бам. В соответствии с этим рис. 13 в первом приближении МО­
жет быть использован как для горизонтальных, так и для вер­тикальных труб.

В. Кох в своих исследованиях по теплоотдаче от труб при их наклонном или вертикальном положении показал, что к ним не применима теория подобия, очевидно, потому, что при наклонном положении возникают самые различные поля скоростей.

Для очень тонких цилиндров (проволока) значения[62] указан­ные на рис. 14 и получаемые из уравнения (233), неприемлемы.

А. Е. Кеннели, С. А. Райт я И. С. ван Булейельт * наследовали теплоотдачу от трех различных проволок 0,01143; 0,02616 и

0, 06907 см при различных давлениях и разностях температур до 180°. Они для теплоотдачи проводом длиной 1 см - нашли1 формулу:

3/—

<3 = (4 + 64<2) Ю3 • р°'9 ■ (/х— t2) чаЬтвШвл/см, (229)

Где с? —диаметр, см; р — давление, «мегабер» ( = 750,1 мм рт. ст.); «аЬшаиэ» — по-видимому, 10~3 вт. Если после этого уравнение (229) представить в технической системе единиц и пе­рейти, к коэффициенту теплоотдачи, то для теплоотдачи от тон­кой проволоки путем конвекции в воздухе при давлении в 1 атм получим

Ак = 17,5 Н—ккал/м2-час-°С. (229а)

<х

В соответствии с этим коэффициент теплоотдачи у очень тонких проволок растет примерно обратно пропорционально их диамет­ру, который здесь измеряется в метрах.

В. Нуссельт [63] на основании измерений Форбеса, Кардани, Боттомлея, Кеннели нашел, что коэффициент теплоотдачи кон­векцией у проволок диам. от 0,1 до 0,3 мм обратно пропорцио­нален их диаметру:

Ак = 0,04 ккал/м2-час^С. (230)

<1

Коэффициент теплоотдачи, рассчитанный по этому уравнению, в два-три раза больше коэффициента теплоотдачи, рассчитанно­го по уравнению (229а). Для диаметра меньше 0,1 мм уравнение (229а), видимо, дает лучшие результаты по сравнению с урав­нением (230).

Теплоотдача пластин в спокойном воздухе

Пластину можно рассматривать как часть стенки трубы бес­конечно большого диаметра. Поэтому в первом (приближении к пластинам применимы коэффициенты теплоотдачи, которые были даны выше для труб большого диаметра. Разумеется, это спра­ведливо с определенными ограничениями для горизонтальных пластин, так как у горизонтальной трубы верхние и нижние части омываются воздушным потоком по-разному, что является »резуль­татом нагревания. П. Розин [64] нашел, что при изменении распо­ложения гладкой поверхности теплоотдача от нее изменяется незначительно. Если обозначить теплоотдачу конвекцией и излу­чением при вертикальном положении через единицу, то теплоот­дача при горизонтальном положении поверхности, обращенной вниз, составила 0,957, а при горизонтальном положении поверх­ности, обращенной вверх, она равнялась 1,058. Следовательно, го­ризонтально расположенные поверхности, обращенные вверх, должны иметь теплоотдачу. примерно на 6% выше по сравнению с вертикально расположенными поверхностями.

В. Юргес исследовал теплоотдачу от гладкой вертикальной стенки размером 0,5 X 0,5 м2 в спокойном и движущемся воздухе. Температура пластины менялась в интервале от 46 до 60° С при температуре окружающего пространства 20° С. Юргес нашел а = 5 ккал/м2 *час*0С, что удовлетворительно совпадает со зна­чениями, получаемыми из формулы Нуссельта,

(231)

В. Нуссельт вывел уравнение (231) опытнк.. путем, экспери­ментируя на трубе высотой 0,5 м и диам. 0,09 м при температу­рах поверхности в интервале от 27 до 109° С. При измерении теп­лоотдачи от шара диам. 0,7 м он нашел, что ак при небольших разностях температур ^ — Ь между поверхностью и окружающей средой не подчиняется больше уравнению (231), а стремится к постоянному предельному значению, равному 3. Для разности температур ниже 15° Нуссельт нашел, что

(232)

А = 3,0 + 0,08 (/x — 12) ккал/ім2 • час • °G.

Необходимо участь, что измерения делались лишь на пластинах и

Трубах высотой 0,5 м. Поэтому надо принимать во внимание, что у »вертикальных труб коэффициент теплоотдачи на нижнем конце значительно изменяется, быстро уменьшаясь от максимального
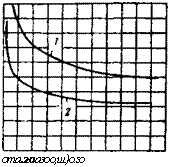
значения (по результатам опытов Коха). Поэтому необходимо знать изменение коэффициента теплоотдачи по высоте пластины. Такие измерения были выполнены В. Нуссельтом и В. Юргесом, а позднее с большей тщатель­ностью Е. Шмидтом и Г. Бек - « ^ п манном. Результаты этих из - 9 мерений графически изобра - § § g жены на рис. 16. Видно, что 7 коэффициент теплоотдачи сна - Ч" s чала быстро, затем медленно 11 J падает и на высоте более £

От а.20 азо о, ш) o. so

40 см от нижнего края дости - 5 J гает постенного значения. 2 Однако значения, полученные g'S /

Нуссельтом и Юргесом, ле - ^

Жат на 50% выше значений 0 „ „

Т7Т г тт Высота от нижнею края

Шмидта и Бекманна. Частично пластины н. м

Это, по-видимому, объясняет-' Рис 16 Изменеиие К0Эффициента теп.

СЯ тем, 4ГО пластина, §зятая лоотдачи для вертикально располо-

Шмидтом И Бекманном, была женцой пластины по данным:

Особенно гладкой (алюминий). t — Нуссельта и Юргеса; 2 - Шмидта тт 1 , и Бекманна

Для среднего коэффициента теплоотдачи в случае верти­кального расположения пластин Шмидт и Бекманн пришли к следующей формуле: __________

А = 4,80 1/ . т / —— ккал/м2- час• °С (233)

V Т0Н у 760 ' 7

- »,

Или при нормальном атмосферном давлении (Ь — 760 мм рт. ст.)

*/~1Г

А = 4,80 1/ ккал/м2-час-°С (233а)

В этом уравнении:

At—разность между температурами пластины и окружающего воздуха, °С;

Т0 — абсолютная температура окружающего воздуха, °К; •

Н—высота пластины, м b — давление воздуха, мм рт. ст.

Сравнивая формулы (231) и (233а), видим, что уравнение (233 а) должно быть точнее в том отношении, что оно отражает 'влияние высоты и абсолютной температуры. Влияние еще более важной величины—разности температур совпадает в обеих фор­мулах: в том и другом случае она дана под корнем четвертой степени. Уравнение (233 а) дает тот же самый коэффициент теп­лоотдачи, что и (231), если высота стенки при температуре воз*-
духа 50° С составляет 0,07 м или если температура воздуха при высоте стенки 0,5 м равна 45°.

Прежде чем перейти к рассмотрению дальнейших, очень важ­ных измерений, применим уравнение (233 а) к шероховатым стен­кам. Кроме того, необходимо еще добавить, что при высоте 0,5 ж, согласно В. Коху, коэффициент теплоотдачи в некоторых случа­ях при своем изменении ’Проходит минимум и во всяком случае далее с увеличением высоты не уменьшается. В соответствии с этим для технических, шероховатых, вертикально расположенных стенок средний коэффициент теплоотдачи конвекцией в свобод­ном воздухе при атмосферном давлении будет райен

(2336)

Ак = 6 1 / ккал/м2 • час • °С.

V ту#

Если (результаты, вычисленные (по этой формуле, сравнить с ве­личинами, полученными Кохом для вертикальных труб (см. табл. 4), то находим, что при высоких разностях температур ре­зультаты в обоих случаях совпадают. Следовательно, влияние разности температур при ее больших значениях должно быть все - таки более значительным. Вероятно, это происходит потому, что при более высоких разностях температур наблюдается нисхо­дящее движение в воздушном потоке, которое существенно увели­чивает коэффициент теплоотдачи.

В табл. 4 происходит неожиданное повышение коэффициента теплоотдачи у трубы диам. 100 мм между 91,4 и 126,9°, т. е. при разности температур М в интервале от 71 до 107° С. В соответ­ствии с этим уравнение (2336) можно применять лишь до зна­чения разности температур, равного 80° С, т. е. если считать тем­пературу воздуха равной 20° С до температуры стенки 100° С. Выше этого значения лучше руководствоваться данными, приве­денными на рис. 14 и в табл. 4.

Свободная конвекция в воде

»Grцber — E’rk — Grigull: Grundgesetze der Wдrmeьbertragung. 3 Neubearb. Aufl. Berlin—Gцttingen—Heidelberg, 1955, S. 282.

(234)

Для коэффициента теплоотдачи в (случае горизонтальной тру­бы, лежащей в 1воде, Н. Григуллем * дается следующая прибли­женная формула:

Где К — функция средней температуры /Ср=—° °° , где

/ст —температура стенки трубы и —температура воды на большом расстоянии, т. е. температура воды, не находящейся под влиянием трубы; d — диаметр трубы, м. Для величины К Гри - гулль в таблице дает числовые значения в интервале температур t^T =20 и tCT =250° С. Эти значения можно получить также из простой температурной функции [65]

К= 16+ 17,85 J/Z^.

Если эту функцию подставить в уравнение (234) и разность температур tcl — ^ обозначить через At, то уравнение (234) преобразуется следующим образом:

1 /------------------ '	К КГ
А = (16+ 17,85 уЧр	1/ -------- ккал/м2-час - С.
' у d

(234а)

Правда, уравнение (234) установлено для горизонтальной трубы, температура стенки которой выше температуры воды, так что, следовательно, /Ст — будет иметь положительное значение. Но, судя ino смыслу, оно также юправедлийо, если /ст меньше, чем too. Однако в этом случае по-прежнему необходимо брать положительное значение Д^, так что At в уравнении (234а) является «абсолютным значением» разности температур стенки трубы — .воды. Если в »качестве примера рассматривать трубу диам. 20 мм, температура которой составляет 100° С, а темпера­тура воды 30°, то ^Ср =65° С и А/=70° С; следовательно, из урав­нения (234а)

А~ 1230 ккал/м2'Час-°С.

Чтобы получить приближенные значения, можно применять уравнение (234а) не только для труб, горизонтально расположен­ных в воде, но и для других тел, если, конечно, применять его разумно, т. е. подставлять соответствующее значение диаметра и учитывать, являются ли (конвективные потоки совершенно сво­бодными * или они встречают на своем пути препятствия [66].

Из сравнения табл. 4 и данных рис. 14 видно, что при свобод­ной конвекции результаты, полученные для горизонтально распо­ложенных труб в потоке воздуха, мало отличаются от результа­тов для труб, расположенных вертикально. Следовательно, мож­но сказать, что уравнение (234а) в большинстве случаев с достаточной точностью применимо для вертикальных труб в спокойной воде [67].

Теплоотдача от наклонных поверхностей к пленке воды

В практике часто встречаются случаи, когда горячие поверх­ности охлаждаются путем орошения их водой. При этом речь идет об особом случае вынужденной конвекции.

Л. Гарвин и Е. В. Келли и др. [68] исследовали эту теплоотдачу с помощью латунной пластины размером 200 X 750 мм, обогре­ваемой. с одной (стороны шаром, наклон которой регулировали от 10 до 90°. Равномерность пленки воды поддерживали с помощью большого числа сопел, расположенных на успокоительном участ­ке длиной 100 мм, температуру воды измеряли медь-константа- новыми термопарами и термометрами. Количество воды измеря­ли ее накоплением (по разности давления между накопленной водой и четыреххлористым углеродом). Температуру пластины, значения которой колебались между 35 и 65° С, измеряли заче - каненными в нее термопарами. Измеренные коэффициенты теп­лоотдачи колебались от 4000 до 9000 ккал/м2■ час-°С. Они зави­сели в первую очередь от расхода воды б в килограммах на каждый метр ширины пластины (в час), следовательно, кг/м • час, и от угла наклона. пластины <р. По Гарвину и Келли, после пере­
счета в систему м-кг-час с достаточной точностью можно при­нять, что

SHAPE \* MERGEFORMAT

Чо,2-Лс:

(235)

370 (sin 9) [69] 1/ G ккал/м2*час-°С.

Следует ожидать, что а также зависит от температуры, а именно, с повышением температуры значение а должно возрасти, так как вязкость воды всегда уменьшается с повышением темпе­ратуры. Но, очевидно, это явление перекрывается влиянием рас­хода среды.