Рис. 37.

Исследование САР на АВМ освобождает от длительных и тру­доемких расчетов, создает условия для более детального и всесто­роннего изучения системы регулирования микродозирования, а так­же позволяет уточнить аналити­ческие расчеты.

гулироівания <на | АВМ імикродози - рования жидкости іпроводилось для двух случаев: без учета внеш­него возмущения и для комбини­рованной системы.

Для системы - регулирования без учета 'возмущения при нулевых начальных условиях согласно структурной схеме (рис. 37) можно написать следующие соотноше­ния между. переменными:

ХРі = ХР — ХР2;

ХР2 = Wn (р) уР , (22)

ур = Wn (p)xPt.

Выбираем масштабы:

хР = рхРх; ХРХ = х. хр Хи хр2 = рхр х2 сРо = ъср с0;

ср1 = Hvf сь ур = V-урУ* Ур = Мр у tP= p-tpt7

где у и у — соответственно первая и вторая производные.

Примем

ьхр = РХР = VахР — = Рср = РуР = ^ уР = РуР ~ 1 ’ Рчр —

где хр хри хр,2 и yv—реальные переменные; tр — реальное время процесса регулирования; х; х\ х2 и у — машинные переменные.

Подставляя значения передаточных функций и вводя масштаб­ные множители, получаем:

(23)

Х = X — Хг х2 =7о у + Сгу;

у = 7,6е~г>8ВРХ1 — 12,84 у — 42,2 у.

На машине ЭМУ-10 решены дифференциальные уравнения (23) с начальными условиями

1Г(0) = ~у (0) = у (O’) = 0;

Xi(t — 1,83) = 0 при 0 ^ t ^ 1,83;

Х2 (0) ==0; f 0 при t = 0;

0,00984 при t > 0.

Найдено ср0=!5,ОО; с*Ч=50,00; tp = 12 мин,

Подставляя значения постоянных коэффициентов для значения Со и Си получаем:

хрх = хр — хР2; Ї

хр2 = 50(/Р + 15уР; 1 (24)

ур = 7,6б-Ь8зрхР — 12,84f/P — 42,2І/Р. j

Следует указать, что с целью проверки правильности решения задачи на модели снимались значения всех переменных для момен - tgb времени /м = /мі; ^м2*, ^мз, ..tмп и подставлялись в уравнения (24). Вычисленные разности между левой и правой частями урав-

Рис. 38.

нения были очень незначительны. Для осуществления такой провер­ки структурная схема несколько изменялась.

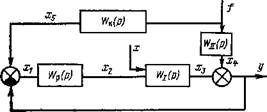
Исследование процессов регулирования в комбинированной сис­теме на АВМ проводилось согласно структурной схеме на рис. 38. Составляем следующую систему уравнений:

Xl =* (#5 + у)

(25)

х2 = Wp(p)Xu хв = WY (р) х2;

я* = (р) f>

хь = Wk (р) f;

У = х з + х4. j

Подставляя выражения передаточных функций и производя не­которые простые преобразования, получаем:

Xi = — Хь — У,

После решений системы дифференциальных уравнений относи­тельно выходного параметра у получим:

1

У— Хз-|-х4 = (0,07x2 — 7хз) —

Г

+ -------------- 5,9х4. (27)

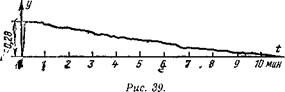
Процесс регулирования комбинированной системы иллюстриру­ется на рис. 39.

Сравнение кривых процессов регулирования, полученных при моделировании, показывает, что амплитуда колебаний выходных координат комбинированной системы по сравнению с одноконтурной системой уменьшается на 12,5%, а время переходного процесса сокращается на 2,8 мин и составляет 10 мин.

Значительное уменьшение динамических отклонений и существенное сокращение длительности переходного процесса в системе с оптимальным воздействием по возмущению свидетельствуют о том, что инвариантная система регулирования микродозирования имеет преимущества относительно одноконтурной системы регулирования по отклонению.

Результаты моделирования процесса микродозирования дали возможность проверить и уточнить правильность аналитических расчетов и выбрать рациональную схему регулирования микродозиро­вания.

Известно, что реально действующая система автоматического регулирования в силу многих причин всегда отличается от расчет-

Таблица 3 Канал Передаточная функция САР до эксплуатации | после эксплуатации Регули­ рования 0,00652-ьзо р 0,00984<?-Ь8зр TV7 і wl (Р) — 9,50/72+4,2/7+1 ’ МЛ мА-мин WI Р> — 12,84/72+5,42/7+1 * мл мА-мин Возму­ щения 0,0180^-0,2зр ТТ7Т / ; 0,0240е-°>5Р WU р> — 4,31 /72+2,26/7+1 ’ мл wn Р) — 5,71 /72+3,96/7+1 ’ МЛ мм рт. ст.-мин мм рт. ст.-мин

Таблица 4 Условие Одноконтурная САР с учетом внешних возмущений Комбинированная САР эксперимента до эксплуатации после эксплуатации до эксплуатации после эксплуатации

Малые возмуще­ния вектора пара­метров относитель­но номинального значения

w*h

		'Ґ
9,10	мин

Большие возму­щения вектора па­раметров от номи­нального значения

	*
9,35	мин

мин

9,30

Понижение по­рядка модели

*/0,150

6,50

ной. В условиях производства параметры элементов всякой реально выполненной системы не совпадают с расчетными: стабильность эле­ментов нарушается под воздействием таких факторов, как, напри­мер, температура, ударные нагрузки, колебания нагрузки, которые с течением времени изменяются и соответственно изменяют динами­ческие свойства системы.

Чтобы выяснить, будет ли реальная система с возможными отклонениями ее параметров от начальных значений удовлетворять предъявляемым требованиям, необходимо проанализировать влия­ние этих отклонений на поведение системы.

Были рассмотрены различные схемы регулирования микродо­зирования и их модели, проведены исследования влияния настройки параметров этих систем к изменениям параметров объекта.

'При исследовании САР микродо­зирования на ЭМУ40 были использованы ранее полученные результаты и результаты исследова­ния работы микродозатора после его длительной эксплуатации.

Длительная эксплуатация микродозатора показывает, что с те­чением времени он изменяет свои динамические характеристики в результате химической реакции, происходящей в электролизере. Это явление объясняется тем, что электролит со временем стано­вится загрязненным и поверхность электрода покрывается окисной пленкой. С целью уточнения влияния этого явления на качество САР микродозирования и определения соответствующей математи­ческой модели динамики микродозатора было проведено повторное исследование после его длительной эксплуатации i*a эксперименталь­ной установке, представленной на рис. 31.

Экспериментальное исследование динамических характеристик микродозатора было проведено по всем каналам регулирования и возмущения.

На основе полученных экспериментальных данных были опре­делены передаточные функции по всем каналам, которые представ­лены в табл. 3.

Результаты исследования чувствительности САР микродозиро­вания представлены в табл. 4.