The total enhancement integrated over wavelength, rather than the enhancement at the resonance wavelength, is relevant for many practical devices. On resonance, the emission is enhanced along the axis of the cavity. However, sufficiently far off resonance, the emission is suppressed. Because the natural emission spectrum of the active medium (without a cavity) can be much broader than the cavity resonance, it is, a priori, not clear whether the integrated emission is enhanced at all. To calculate the wavelength-integrated enhancement, the spectral width of the cavity resonance and the spectral width of the natural emission spectrum must be determined. The resonance spectral width can be calculated from the finesse of the cavity or the cavity quality factor.

The theoretical width of the emission spectrum of bulk semiconductors is 1.8 kT (see, for example, Schubert, 1993), where k is Boltzmann’s constant and Tis the absolute temperature. At room temperature, 1.8 kT corresponds to an emission linewidth of AX„ = 31 nm for an emission wavelength of 900 nm. For a cavity resonance width of 5-10 nm, one part of the spectrum is strongly enhanced, whereas the rest of the spectrum is suppressed. The integrated enhancement ratio (or suppression ratio) can be calculated analytically by assuming a gaussian natural emission spectrum. For semiconductors at 300 K, the linewidth of the natural emission is, in the case of high-finesse cavities, larger than the width of the cavity resonance. The gaussian
emission spectrum has a width of AV = 2a (2 ln 2)1/2 and a peak value of (a (2n)12)-1, where a is the standard deviation of the gaussian function. The integrated enhancement ratio (or suppression ratio) is then given by (Hunt et al., 1993)

(14.22)

Gint = v Ge A^—I— = GeT^M

2 ov 2п AAn

where the factor of n / 2 is due to the lorentzian lineshape of the enhancement spectrum. Hence, the integrated emission enhancement depends on the natural emission linewidth of the active material. The value of Gint can be quite different for different types of optically active materials. Narrow atomic emission spectra can be enhanced by several orders of magnitude (Schubert et al., 1992b). On the other hand, materials having broad emission spectra such as dyes or polymers (de Martini et al., 1987; Suzuki et al., 1991) may not exhibit any integrated enhancement at all. Equation (14.22) also shows that the width of the resonance has a profound influence on the integrated enhancement. Narrow resonance spectral widths, i. e. high finesse values or long cavities (Hunt et al., 1992), reduce the integrated enhancement.

Example: Spectral enhancement and integrated enhancement of a resonant-cavity structure. As an example, we calculate the spectral and wavelength-integrated enhancement of a semiconductor resonant - cavity structure using Eqs. (14.21) and (14.22). With the reflectivities R1 = 90% and R2 = 97%, an antinode enhancement factor of £ = 1.5 and xcav / т « 1, one obtains a finesse of F = 46, and a peak enhancement factor of Ge = 68 using Eq. (14.21). Insertion of this value into Eq. (14.22), using a cavity resonance bandwidth of AA = 6.5 nm (Schubert et al., 1994), and the theoretical 300 K natural emission linewidth of AA = 31 nm, one obtains a theoretical integrated enhancement factor of Gint = 13. Experimental enhancement factors of 5 have been demonstrated (Schubert et al., 1994) for the reflectivity values assumed above. The lower experimental enhancement is in part due to a broader natural emission linewidth, which exceeds the theoretical value of 1.8 kT.

The spontaneous emission spectrum of a bulk semiconductor is shown schematically in Fig. 14.3 (b). For maximum enhancement along the cavity axis, the cavity must be in resonance with the natural emission spectrum. Note that additional broadening mechanisms, such as alloy broadening, will broaden the natural emission spectrum over its theoretical value of 1.8 kT. Quantum well structures have inherently narrower spectra (0.7 kT), due to the step-function-like density of states. Low temperatures and excitonic effects can further narrow the natural emission linewidth. Thus, higher enhancements are expected for low temperatures and quantum well active regions.

14.2 Experimental emission enhancement and angular dependence Particularly high spontaneous emission enhancements can be attained with emitters that have naturally narrow emission lines. Atomic transitions, as in rare-earth elements, have such narrow emission lines. For this reason, rare-earth doped cavities are a great system to study the emission enhancement. The emission spectrum of a high-finesse Si / SiO2 cavity with an erbium-doped SiO2 active layer is shown in Fig. 14.4 (Schubert et al., 1992b). A distinct narrowing of the Er emission spectrum and a giant enhancement of the emission was found. The enhancement factor was greater than 50, when compared to a non-cavity structure.

1 Si/Si02:Er	і
- Resonant cavity	—
T= 295 К
--- With cavity
_----- Without cavity	-
1DRR	5 meV -
ц j VJ L)I Si02:Er	X 1
11 DBR	- 1
	I 1
Silicon	'V-v X 10 -
	> _ -

— ca

1450 1500 1550 Wavelength X (nm)

1600

Fig. 14.4. Photoluminescence spectra of Er-doped SiCb. One of the spectra is for Er-doped Si02 located in a cavity resonant at 1540 nm. The other spectrum is without a cavity. An emission enhancement factor greater than 50 is found (after Schubert et al., 1992b).

The cavity consisted of a 4-pair Si / SiO2 bottom DBR with a calculated reflectivity of 99.8%, the Er-doped X / 2 thick SiO2 active layer, and a 2.5-pair Si / SiO2 top DBR with a calculated

reflectivity of 98.5%. The SiO2 active layer was doped with Er of dose 7.7 x 1015 cm-2. The

measured cavity finesse was F = 310, slightly lower than the calculated finesse of 370.

The peak emission wavelength depends on the emission angle. The angular dependence can be derived from the condition that the normal wave vector, k±, must be constant (in resonance with the cavity), independent of the k propagation direction. This condition can be written as

k cos 9 = ky (14.23)

or

2n cos 9 = (14.24)

Xe(9) X res

where ^res and Xe are the resonance and emission wavelengths, respectively, and 9 is the angle inside the cavity with respect to the surface normal (polar angle), as illustrated in Fig. 14.5.

	к	Refractive index = 1.0
і	*11	---- к 1 A
		/ j Refractive
		Q / 1 index = n
		7 » і к

R

R

Fig. 14.5. Perpendicular and parallel component of wave vector к for light propagating in a resonant cavity.

Using Eq. (14.24) and Snell’s law (n sin 9 = sin 0), the emission wavelength is given by

arcsin I — sin 0

(14.25)

n

Xe — Xres cos

For small angles, the equation can be approximated by

0

X

1 -

res

2n

(14.26)

The angular dependence of the peak emission wavelength is shown in Fig. 14.6. The solid and dashed lines are the exact (Eq. 14.25) and approximate solutions (Eq. 14.26), respectively. A refractive index of 1.5 is used in the calculation.

' і ' ■ Si/SiCb Resonant cavity " Active: SiCb:Er ’ T= 295 К	'
L и l > < . і		- V
111!' n> N	Ws [1-1(1 Exact soli і	X -)2i^ / ч ition —/ - .

1550

10 20 Angle ©о (°)

1600

sb с и о > $■

Fig. 14.6. Peak emission wave­length as a function of polar angle for a planar Si/SiCbiEr resonant cavity (after Schubert et al1992b).

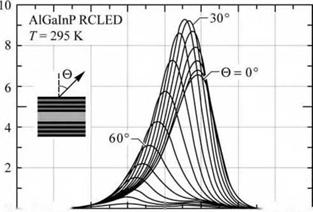
A similar angular dependence is found for semiconductors. The emission spectra of an AlGaInP cavity are shown in Fig. 14.7 for different emission angles (Streubel et al., 2002). Note that the highest intensity is found at an emission angle of 30°, indicating that the resonance wavelength of the cavity is located at the long-wavelength end of the semiconductor natural emission spectrum. This results in the highest angle-integrated emission power (Streubel et al., 2002).

Fig. 14.7. Emission spectra of Al - GalnP RCLED for different polar angles. The long-wavelength part of the QW emission is emitted in the forward direction (0°). The shorter wavelengths are emitted off-axis. When measured with an integrating sphere, an 18 nm wide spectrum (FWHM) is found (after Streubel et al., 2002).

0 ' 1 1 1 1 1 610 620 630 640 650 660 670 680 690 Wavelength X (nm)